数据分析实战 | 贝叶斯分类算法——病例自动诊断分析

目录

一、数据及分析对象

二、目的及分析任务

三、方法及工具

四、数据读入

五、数据理解

六、数据准备

七、模型训练

八、模型评价

九、模型调参

十、模型预测

---

一、数据及分析对象

CSV文件——“bc_data.csv”

数据集链接：https://download.csdn.net/download/m0_70452407/88524905

该数据集主要记录了569个病例的32个属性，主要属性/字段如下：

（1）ID：病例的ID。

（2）Diagnosis（诊断结果）：M为恶性，B为良性。该数据集共包含357个良性病例和212个恶性病例。

（3）细胞核的10个特征值，包括radius（半径）、texture（纹理）、perimeter（周长）、面积（area）、平滑度（smoothness）、紧凑度（compactness）、凹面（concavity）、凹点（concave points）、对称性（symmetry）和分形维数（fractal dimension）等。同时，为上述10个特征值分别提供了3种统计量，分别为均值（mean）、标准差（standard error）和最大值（worst or largest）。

二、目的及分析任务

理解机器学习方法在数据分析中的应用——采用朴素贝叶斯算法进行分类分析。

（1）以一定比例将数据集划分为训练集和测试集。

（2）利用训练集进行朴素贝叶斯算法的建模。

（3）使用朴素贝叶斯分类模型在测试集上对诊断结果进行预测。

（4）将朴素贝叶斯分类模型对诊断结果的分类预测与真实的诊断结果进行对比分析，验证朴素贝叶斯分类模型的有效性。

三、方法及工具

Python语言及scikit-learn包。

四、数据读入

import pandas as pd
df=pd.read_csv("D:\\Download\\JDK\\数据分析理论与实践by朝乐门_机械工业出版社\\第4章 分类分析\\bc_data.csv"
                   ,header=0)
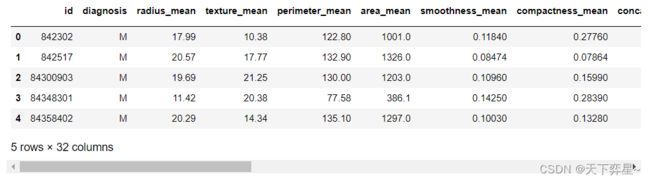
df.head()

五、数据理解

查看数据集中是否存在缺失值，可以使用pandas包的isnull()方法判断数据是否存在空值，并结合any()方法查看每个特征中是否存在缺失值。

df.isnull().any()

id                         False
diagnosis                  False
radius_mean                False
texture_mean               False
perimeter_mean             False
area_mean                  False
smoothness_mean            False
compactness_mean           False
concavity_mean             False
concave points_mean        False
symmetry_mean              False
fractal_dimension_mean     False
radius_se                  False
texture_se                 False
perimeter_se               False
area_se                    False
smoothness_se              False
compactness_se             False
concavity_se               False
concave points_se          False
symmetry_se                False
fractal_dimension_se       False
radius_worst               False
texture_worst              False
perimeter_worst            False
area_worst                 False
smoothness_worst           False
compactness_worst          False
concavity_worst            False
concave_points_worst       False
symmetry_worst             False
fractal_dimension_worst    False
dtype: bool

从输出结果可以看出，数据集中不存在缺失值。

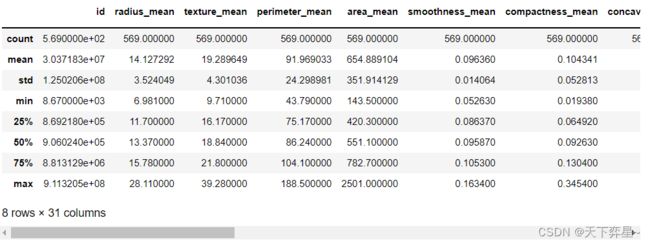
对数据框df进行探索性分析，这里采用的实现方式为调用pandas包中数据框的describe()方法。

df.describe()

除了describe()方法，还可以调用shape属性对数据框进行探索性分析。

df.shape

(569, 32)

六、数据准备

本项目的分类任务属于二分类任务，需要将数据框df中诊断结果“diagnosis”的值转换为0和1的数值类型，这里使用scikit-learn包中preprocessing模块的LabelEncoder()方法。

from sklearn.preprocessing import LabelEncoder
encoder=LabelEncoder()
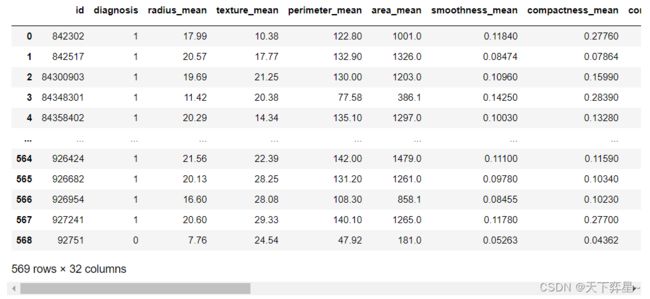
df['diagnosis']=encoder.fit_transform(df['diagnosis'])
df

可以看出原先诊断结果diagnosis从M（表示恶性）和B（表示良性）转换成1（表示恶性）和0（表示良性）。

将数据集以7：3的比例分为训练集和测试集，这里首先将细胞核的特征集（即数据框df中除了前两列的数据集）赋值到变量x中，并将诊断结果赋值到变量y中以便后续使用。接着使用scikit-learn包中model_selection模块的train_test_split()方法进行数据集的划分。

from sklearn.model_selection import train_test_split
x=df.iloc[:,2:]
y=df['diagnosis']
x_train,x_test,y_train,y_test=train_test_split(x,y,
                                               test_size=0.3,
                                               random_state=40,stratify=y)

七、模型训练

scikit-learn包中naive_bayes模块里根据特征类型和分布提供了多个不同的模型，如GaussianNB、BernoulliNB以及MultinomialNB。其中：

（1）GaussianNB假设数据符合正态分布，是用于连续值较多的特征。

（2）BernoulliNB是用于二元离散值得特征。

（3）MultinomialNB是用于多元离散的特征。

这里的数据集的特征均为连续变量，因此使用GaussianNB进行模型的训练。

from sklearn.naive_bayes import GaussianNB
gnb_clf=GaussianNB()
gnb_clf.fit(x_train,y_train)

GaussianNB()

八、模型评价

这里使用准确率、精确率、召回率和f1值对模型进行评价，scikit-learn中的metrics模块提供了accuracy_score()、precision_score(),recall_score(),f1_score()方法。

from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
gnb_ypred=gnb_clf.predict(x_test)
print("准确率：%f,\n精确率：%f,\n召回率：%f,\nf1值：%f."
      %(accuracy_score(y_test,gnb_ypred),precision_score(y_test,gnb_ypred)
        ,recall_score(y_test,gnb_ypred),f1_score(y_test,gnb_ypred)))

准确率：0.935673,
精确率：0.964912,
召回率：0.859375,
f1值：0.909091.

九、模型调参

GaussianNB可输入两个参数prior和var_smoothing。prior用于定义样本类别的先验概率，默认情况下会根据数据集计算先验概率，因此一般不对prior进行设置。var_smoothing的默认值为1e-9，通过设置特征的最大方差，进而以给定的比例添加到估计的方差中，主要用于控制模型的稳定性。

这里调用scikit-learn包model_selection模块中的网络搜索功能，即GridSearchCV()方法对模型进行调参。先定义一个变量params来存储alpha的不同取值（这里假设var_smoothing的取值范围为[1e-7,1e-8,1e-9,1e-10.1e-11,1e-12])。

from sklearn.model_selection import GridSearchCV
params={'var_smoothing':[1e-7,1e-8,1e-9,1e-10,1e-11,1e-12]}
gnb_grid_clf=GridSearchCV(GaussianNB(),params,cv=5,verbose=2)
gnb_grid_clf.fit(x_train,y_train)

Fitting 5 folds for each of 6 candidates, totalling 30 fits
[CV] END ................................var_smoothing=1e-07; total time=   0.0s
[CV] END ................................var_smoothing=1e-07; total time=   0.0s
[CV] END ................................var_smoothing=1e-07; total time=   0.0s
[CV] END ................................var_smoothing=1e-07; total time=   0.0s
[CV] END ................................var_smoothing=1e-07; total time=   0.0s
[CV] END ................................var_smoothing=1e-08; total time=   0.0s
[CV] END ................................var_smoothing=1e-08; total time=   0.0s
[CV] END ................................var_smoothing=1e-08; total time=   0.0s
[CV] END ................................var_smoothing=1e-08; total time=   0.0s
[CV] END ................................var_smoothing=1e-08; total time=   0.0s
[CV] END ................................var_smoothing=1e-09; total time=   0.0s
[CV] END ................................var_smoothing=1e-09; total time=   0.0s
[CV] END ................................var_smoothing=1e-09; total time=   0.0s
[CV] END ................................var_smoothing=1e-09; total time=   0.0s
[CV] END ................................var_smoothing=1e-09; total time=   0.0s
[CV] END ................................var_smoothing=1e-10; total time=   0.0s
[CV] END ................................var_smoothing=1e-10; total time=   0.0s
[CV] END ................................var_smoothing=1e-10; total time=   0.0s
[CV] END ................................var_smoothing=1e-10; total time=   0.0s
[CV] END ................................var_smoothing=1e-10; total time=   0.0s
[CV] END ................................var_smoothing=1e-11; total time=   0.0s
[CV] END ................................var_smoothing=1e-11; total time=   0.0s
[CV] END ................................var_smoothing=1e-11; total time=   0.0s
[CV] END ................................var_smoothing=1e-11; total time=   0.0s
[CV] END ................................var_smoothing=1e-11; total time=   0.0s
[CV] END ................................var_smoothing=1e-12; total time=   0.0s
[CV] END ................................var_smoothing=1e-12; total time=   0.0s
[CV] END ................................var_smoothing=1e-12; total time=   0.0s
[CV] END ................................var_smoothing=1e-12; total time=   0.0s
[CV] END ................................var_smoothing=1e-12; total time=   0.0s
GridSearchCV(cv=5, estimator=GaussianNB(),
             param_grid={'var_smoothing': [1e-07, 1e-08, 1e-09, 1e-10, 1e-11,
                                           1e-12]},
             verbose=2)

这里在GridSearchCV()方法中传入了GaussianNB模型、需优化的参数取值变量params、交叉验证的参数cv（这里设置了五折交叉验证）以及显示训练日志参数verbose（verbose取值为0时不显示训练过程，取值为1时偶尔输出训练过程，取值>1时对每个子模型都输出训练过程。

接着使用GridSearchCV中的best_params_查看准确率最高的模型参数。

gnb_grid_clf.best_params_

{'var_smoothing': 1e-10}

由此可知，在给定的var_smoothing取值范围内，当取值为1e-10时模型的准确率最高。

十、模型预测

模型的预测可通过训练好的模型的predict()方法使用，这里使用默认的情况下和调参后 的两个GaussianNB模型对测试集进行分类预测，并使用模型评价方法进行比较。

首先使用默认情况下的GaussianNB对测试集进行分类预测，然后将分类结果存储到变量gnb_ypred中，并输出模型的准确率、精确率、召回率以及f1值。

gnb_ypred=gnb_clf.predict(x_test)
print("准确率：%f,\n精确率：%f,\n召回率：%f,\nf1值：%f."
      %(accuracy_score(y_test,gnb_ypred),precision_score(y_test,gnb_ypred)
        ,recall_score(y_test,gnb_ypred),f1_score(y_test,gnb_ypred)))

准确率：0.935673,
精确率：0.964912,
召回率：0.859375,
f1值：0.909091.

接着，使用调参后的GaussianNB对测试集进行分类预测，然后将分类结果存储到tuned_ypred中，并输出模型的准确率、精确率、召回率以及f1值。

tuned_ypred=gnb_grid_clf.best_estimator_.predict(x_test)
print("准确率：%f,\n精确率：%f,\n召回率：%f,\nf1值：%f."
      %(accuracy_score(y_test,tuned_ypred),precision_score(y_test,tuned_ypred)
        ,recall_score(y_test,tuned_ypred),f1_score(y_test,tuned_ypred)))

准确率：0.941520,
精确率：0.965517,
召回率：0.875000,
f1值：0.918033.

tuned=GaussianNB(var_smoothing=1e-10)
tuned.fit(x_train,y_train)
tuned_ypred1=tuned.predict(x_test)
print("准确率：%f,\n精确率：%f,\n召回率：%f,\nf1值：%f."
      %(accuracy_score(y_test,tuned_ypred1),precision_score(y_test,tuned_ypred1)
        ,recall_score(y_test,tuned_ypred1),f1_score(y_test,tuned_ypred1)))

tuned=GaussianNB(var_smoothing=1e-10)
tuned.fit(x_train,y_train)
tuned_ypred1=tuned.predict(x_test)
print("准确率：%f,\n精确率：%f,\n召回率：%f,\nf1值：%f."
      %(accuracy_score(y_test,tuned_ypred1),precision_score(y_test,tuned_ypred1)
        ,recall_score(y_test,tuned_ypred1),f1_score(y_test,tuned_ypred1)))

可见，通过调参GaussianNB，在4个评价指标上均得到一定的提高。