数据结构:树、二叉树的概念和性质
树、二叉树
文章目录
- 树
- 树的相关概念
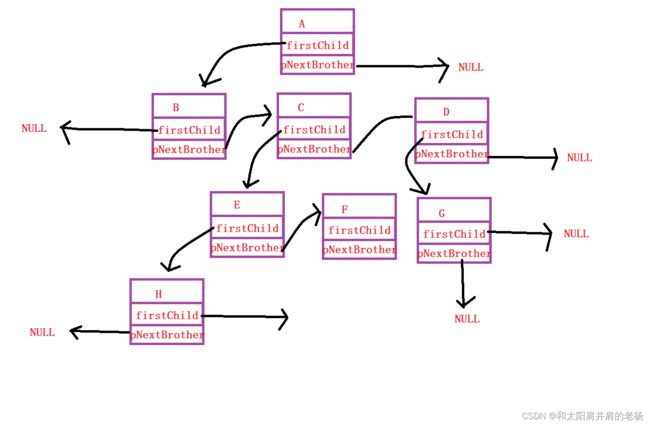
- 孩子兄弟表示法
- 二叉树
- 二叉树的性质
- 二叉树的顺序存储结构
树
树是一种非线性的数据结构。
图A就是一棵树,为什么叫它树呢?因此这个数据的结构十分地像现实当中的树,只不过根在上,叶子朝下而已。在讨论这种结构时,我们将树中的每一个点称为节点,而最开始的点称为根(根节点),当然最开始的点得看你以哪个树作为参照物。例如:
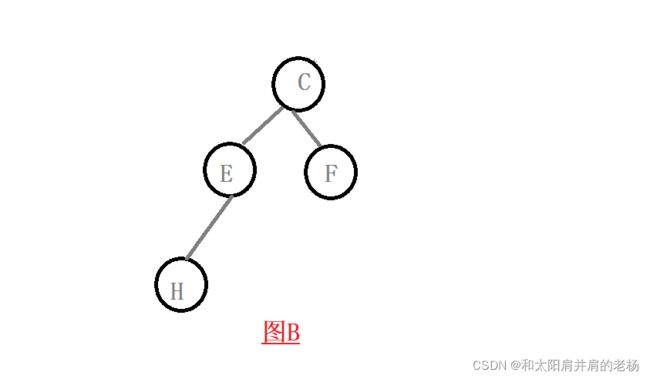
图B中的树被称为图A中的树的其中一棵子树。图A的根节点为A,而图B根节点为C。
【注意】
- 从根节点到每一个节点有且仅有一条路径。 即相邻的节点互不干涉。
- 树的节点有左右之分,即树是有序的。
树的相关概念
【节点的度】
一个节点含有的子树的个数称为该节点的度
如上图:A节点的度为3
【叶节点或终端节点】
度为0的节点称为叶节点。
如上图:B、F、G、H等节点为叶节点。
【非终端节点或分支节点】
度不为0的节点;
如上图:C、D、E等节点为分支节点。
【双亲节点或父节点】
若一个节点含有子节点,则该节点称为其子节点的父节点;
如上图:A是B的父节点。
【孩子节点或子节点】
一个节点含有的子树的根节点称为该节点的子节点;
如上图:B是A的孩子节点。
【兄弟节点】
具有相同父节点的节点互称为兄弟节点;
如上图:B、C是兄弟节点。
【树的度】
一棵树中,树中节点的最大的度称为树的度;
如上图:树的度为3。
【节点的层次】
从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
【树的高度或深度】
树中节点的最大层次;
如上图:树的高度为4。
【堂兄弟节点】
其父节点在同一层的节点互为堂兄弟节点;
如上图:F、G互为兄弟节点。
【节点的祖先】
从根到该节点所经分支上的所有节点;
如上图:A是所有节点的祖先。
【子孙】
以某节点为根的子树中任一节点都称为该节点的子孙;
如上图:所有节点都是A的子孙。
【森林】
多棵树的集合被称为森林;
孩子兄弟表示法
树的表示方法也有很多种,最实用的方法为:孩子兄弟表示法。
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
int _data; // 结点中的数据域
};
二叉树
二叉树是特殊的树。
它的特点是树的度不超过2,例如:
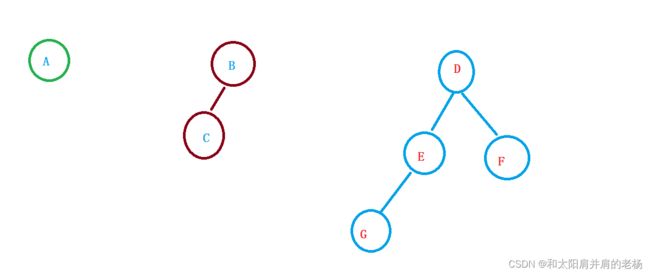
上面的树的度均未超过2,因此均为二叉树。

现实中的这个树便是一棵标准的二叉树。
二叉树是一种特殊的树,而满二叉树和完全二叉树则是一种特殊的二叉树:
【满二叉树】
如果一棵二叉树的每一层节点都达到最大个数,则该树为满二叉树。

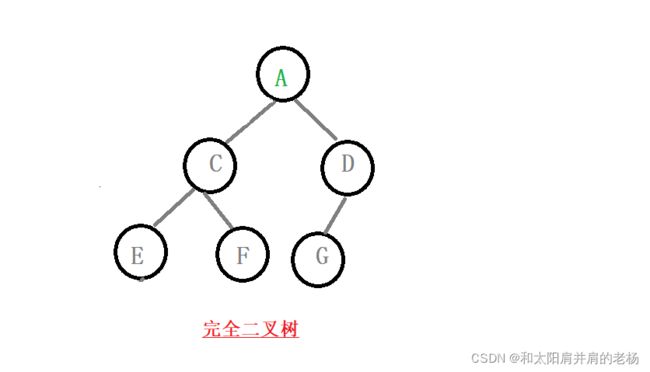
【完全二叉树】
如果一棵二叉树的前N-1层节点个数达到最大,且最后一层的节点是按从左到右的顺序依次排列,则该树为完全二叉树。满二叉树其实也是特殊的完全二叉树。
二叉树的性质
若规定根节点的层数为第一层,则一棵二叉树有以下性质:
- 一棵非空二叉树第i层上的节点最多有2 ^ (i - 1)个。
- 深度为h的二叉树,节点最多有2^h - 1 个。
- 度为0的节点比度为2的节点多1个。
二叉树的顺序存储结构
这种数据的结构逻辑上是一棵二叉树,但是在计算机内对于数据的存储都只能采用顺序存储或链式存储。
【顺序存储】·
顺序存储,也就是采取数组来存储。该结构比较适用于存储完全二叉树。
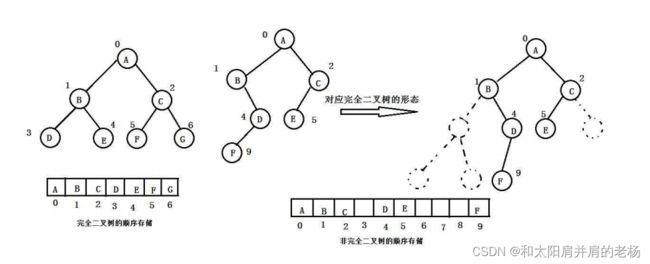
对于非完全二叉树如果采取顺序存储会造成内存空间的浪费,因此比较适合完全二叉树。
根据上图可以得出一个关于二叉树的重要性质:
如果一棵二叉树采取数组的形式存储:设父亲节点的下标为Parent,其左孩子节点的下标为rChild, 右孩子节点的下标为lChild.
![]()
二叉树顺序存储的实现将在下一篇文章介绍。