二叉平衡搜索树-AVL树

1. avl树的概念

前面学习过二叉搜索树，理想状态下虽可以缩短查找的效率，但如果数据有序或接近有序依次插入后二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。
因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

• 它的左右子树都是AVL树
• 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
  

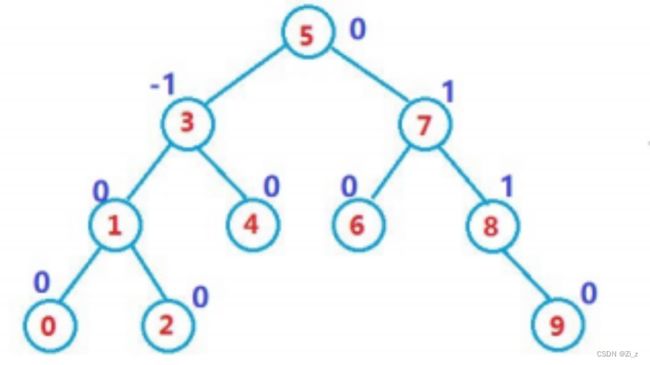
平衡因子的计算一般是右子树的高度-左子树的高度

因此AVL树也叫做二叉平衡树，若树上有n个结点，树的高度可保持在log2N，搜索的次数也就是它的高度次。

2. 树结点的定义

template<class K, class V>
struct AVLTreeNode {
	AVLTreeNode(pair<const K, V>& kv)
		:_kv(kv), _bf(0), _left(nullptr), _right(nullptr), _parent(nullptr)
	{

	}
	pair<const K, V> _kv;	    //key/value模型
	int _bf;					//平衡因子
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	//除了左右指针外还要增加一个指向父节点的指针
	//因为后续插入结点后需要向上调整祖先们的平衡因子
	AVLTreeNode<K, V>* _parent;	
};

3. 结点的插入

avl树插入的第一步和二叉搜索树是一致的，根据搜索树的性质选择一个合适的位置进行插入，不同的是插入完成后，树的平衡性可能会受到破坏，因此需要更新祖先们的平衡因子，若插入在左边parent的平衡因子-1，反之+1，更新后会有三种情况：

1. 平衡因子==0
   这种情况说明parent这颗(子)树的整体高度不变，因此不需要再沿着祖先们的路径往上进行更新。
2. 平衡因子==1 || -1
   这种情况说明parent这颗(子)树的高度发生了变化，因此需要继续沿着祖先们的路径往上进行更新。
3. 平衡因子==2 || -2
   这种情况说明parent这颗(子)树的高度发生变化的同时且不再满足平衡，需要对其进行旋转让其变得平衡。

对于情况三，该如何进行旋转？这里需要分类讨论：

在旋转的时候需要注意的是：

1. 旋转后依然保持它是搜索树。
2. 变成平衡树的同时降低子树的高度。

3.1 左单旋

新节点插入较高右子树的右侧—右右：左单旋：

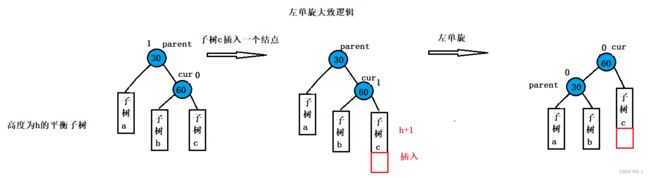
左旋的核心在于要把cur的左子树交给parent的右子树，然后parent作为cur的左子树，旋转完成后还需要修改对应结点父指针的指向和平衡因子。

代码实现：

void rotateLeft(Node* parent) {
	//对于左单旋只与三个结点有关
	//parent、cur(parent->_right)和cur->left
	Node* cur = parent->_right;
	Node* curleft = cur->_left;
	//cur一定不为空而cur->left是有可能为空的
	//因此需要特殊判断
	if (curleft) {
		//指向新parent
		curleft->_parent = parent;
	}
	//核心操作
	parent->_right = curleft;
	cur->_left = parent;	

	//先保存parent的父节点后续会用到
	//然后修改对应父节点的指向
	Node* oldparent = parent->_parent; 
	parent->_parent = cur;
	cur->_parent = oldparent;

	//parent可能是根节点也可能是一颗子树
	//若是根节点那么oldparent则为空
	//cur为新的根
	if (!oldparent) {
		_root = cur;
	}
	//否则判断parent结点是oldparent的哪颗子树
	//让其指向新的孩子cur
	else {
		if (oldparent->_left == parent) {
			oldparent->_left = cur;
		}
		else {
			oldparent->_right = cur;
		}
	}
	//旋转完毕后与插入之前(子)树的高度是不变的，同时还填上了矮的那颗子树
	//因此要修改cur和parent的平衡因子为0
	cur->_bf = parent->_bf = 0;
}

3.2 右单旋

新节点插入较高左子树的左侧—左左：右单旋：

右单旋的逻辑与左单旋非常相似，该逻辑的核心操作在于要把cur的右子树交给parent的左子树，让parent作为cur的右子树，同时旋转完成后 修改对应结点父指针的指向和平衡因子。

代码实现：

void ratateRight(Node* parent) {
	//同样只与三个结点有关
	//parent、cur(parent->_left)和cur->_right
	Node* cur = parent->_left;
	Node* curright = cur->_right;
	if (curright) {
		curright->_parent = parent;
	}
	parent->_left = curright;
	cur->_right = parent;

	Node* oldparent = parent->_parent;
	parent->_parent = cur;
	cur->_parent = oldparent;

	if (!oldparent) {
		_root = cur;
	}
	else {
		if (oldparent->_left == parent) {
			oldparent->_left = cur;
		}
		else {
			oldparent->_right = cur;
		}
	}

	cur->_bf = parent->_bf = 0;
}

3.3 右左双旋

新节点插入较高右子树的左侧—右左：先右单旋再左单旋

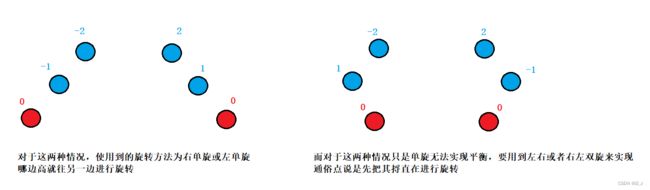
单旋只能解决纯粹是一边高的场景(左左高或者右右高)，对于下面这种场景单旋无法解决：

类似上述这种更为复杂的树结构也是同样的道理，因此要用到双旋解决。

抽象点说若需要旋转的那颗(子)树的结构呈一条直线，那么单旋就可以解决，而若为折线的情况，则要用双旋

对于折线情况，能否先让其"变"成一条直线再进行单旋呢？这里的变就是第一次单旋，旋转为直线后再进行第二次单旋。

第一次旋转如何操作？对于上图的例子，其实就是先以cur为旋转点对cur和新插入的结点进行右单旋(对于这两个结点而言是左边高)，捋直了后就变成了纯粹的一边高，此时再以parent为旋转点对parent和cur进行左单旋：

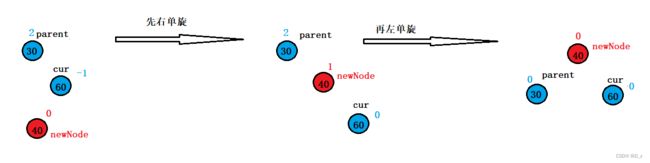
这是最简单的一种情况，稍微复杂点的树结构比如下图，也是需要通过双旋来解决：

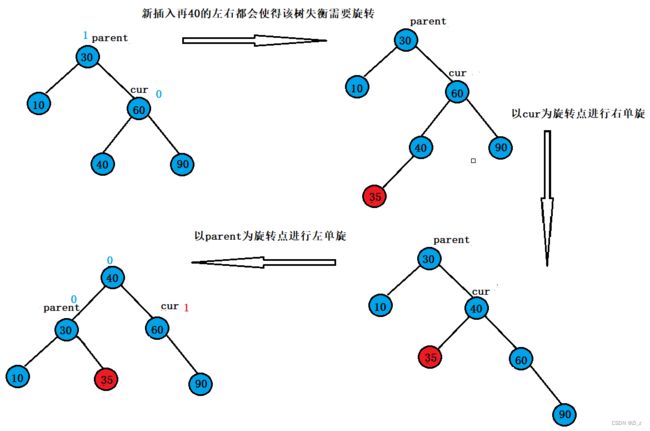
若插入再40结点的右边时旋转后的结构会有什么不同呢？

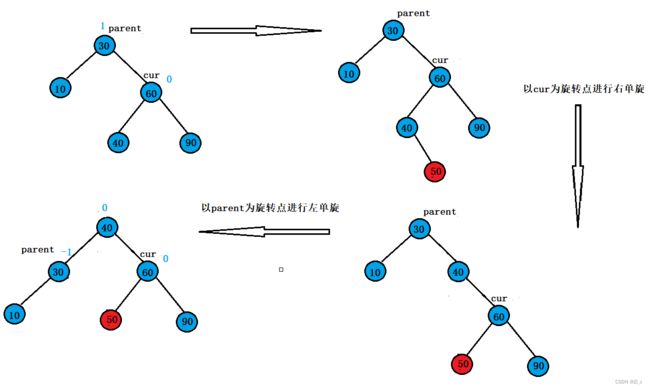
可以发现的是若插入在40的左边时，旋转完成后新节点成了parent的右子树，而插入在右边时最终变成了cur的左子树，parent和cur分别为40这个结点的左右子树，40成了这棵树的根。

对于其它更为复杂的树结构，如下抽象图，解决方法也是同样的道理：

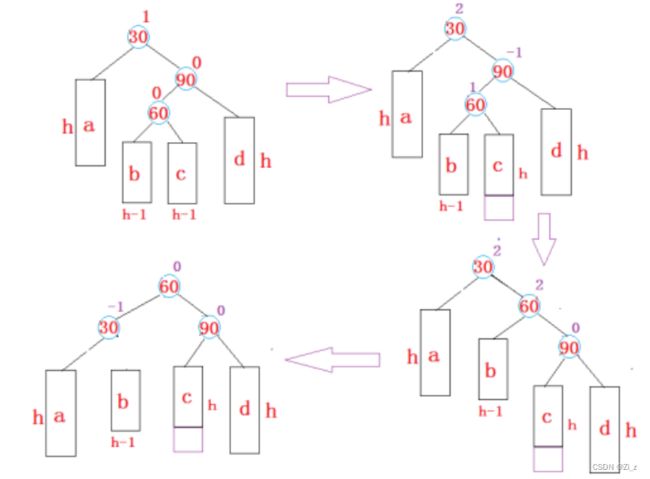
双旋结束后，还需要更新对应结点的平衡因子，根据上面的三个例子，parent和cur平衡因子会有三种情况：

1. parent和cur都为0。
2. parent为0，cur为1。
3. parent为-1，cur为0。

如何区分的关键在于40这个结点是否是新增；在40结点的左边插入；在40结点的右插入。

若平衡因子是第一种情况，那么40是新增结点；若是第二种情况，那么是在40的左边插入新节点；最后一种情况是在40的右边插入新结点。

代码实现：

void rotatRightLeft(Node* parent) {
	//先保存关键结点的平衡因子
	Node* cur = parent->_right;
	Node* curleft = cur->_left;
	int bf = curleft->_bf;

	//复用单旋
	rotateRight(cur);
	rotateLeft(parent);

	//旋转后根据情况更新对应的平衡因子
	//自己就是新增
	if (bf == 0) {
		parent->_bf = cur->_bf = curleft->_bf = 0;
	}
	//在左边插入
	else if (bf == -1) {
		parent->_bf = curleft->_bf = 0;
		cur->_bf = 1;
	}
	//右边插入
	else if (bf == 1) {
		cur->_bf = curleft->_bf = 0;
		parent->_bf = -1;
	}
	else {
		assert(false);
	}
}

3.4 左右双旋

新节点插入较高左子树的右侧—左右：先左单旋再右单旋

左右双旋的情况简单概括为如下三种：

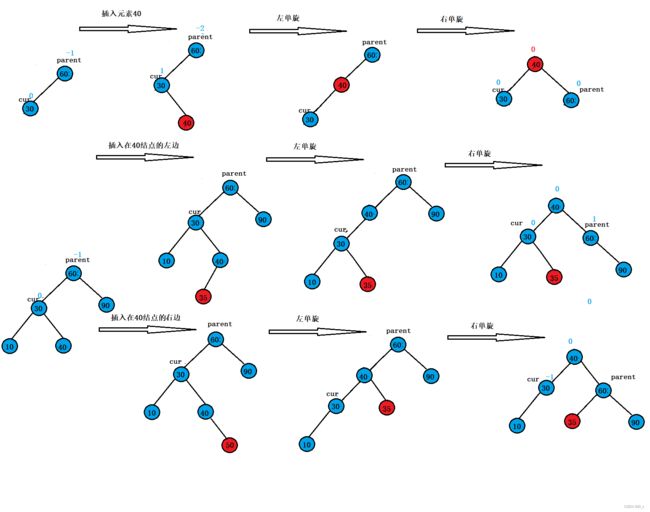
对于左右双旋情况的整体分析是基本与右左双旋一致，直接上代码：

void rotatLeftRight(Node* parent) {
	Node* cur = parent->_left;
	Node* curright = cur->_right;
	int bf = curright->_bf;

	rotateLeft(cur);
	rotateRight(parent);
	
	if (bf == 0) {
		parent->_bf = cur->_bf = curright->_bf = 0;
	}
	//在左边插入
	else if (bf == -1) {
		cur->_bf = curright->_bf = 0;	 
		parent->_bf = 1;
	}
	//右边插入
	else if (bf == 1) {
		parent->_bf = curright->_bf = 0;
		cur->_bf = -1;
	}
	else {
		assert(false);
	}
}

4. 结点的删除(了解)

因为AVL树也是二叉搜索树，可按照二叉搜索树的方式将节点删除，然后再更新平衡因子，只不错与删除不同的时，删除节点后的平衡因子更新，最差情况下一直要调整到根节点的位置，并且调整的过程相比于插入会更加复杂，所以稍微了解就好。

5. 整体代码

#pragma once
#include 
#include 
#include 


using namespace std;

template<class K, class V>
struct AVLTreeNode {
	AVLTreeNode(const pair<const K, V>& kv)
		:_kv(kv), _bf(0), _left(nullptr), _right(nullptr), _parent(nullptr)
	{

	}
	pair<const K, V> _kv;	    //key/value模型
	int _bf;					//平衡因子
	AVLTreeNode<const K, V>* _left;
	AVLTreeNode<const K, V>* _right;
	//除了左右指针外还要增加一个指向父节点的指针
	//因为后续插入结点后需要向上调整祖先们的平衡因子
	AVLTreeNode<const K, V>* _parent;
};

template<class K, class V>
class AVLTree {
	typedef AVLTreeNode<const K, V> Node;
public:
	bool insert(const pair<const K, V>& kv) {
		//首先根据搜索树的性质找到一个合适的位置进行插入
		if (!_root) {
			_root = new Node(kv);
			return true;
		}
		Node* cur = _root, *parent = _root;
		while (cur) {
			if (cur->_kv.first < kv.first) {
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first) {
				parent = cur;
				cur = cur->_left;
			}
			else {
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first) {
			parent->_right = cur;
		}
		else {
			parent->_left = cur;
		}
		cur->_parent = parent;
		//插入完毕后需要沿着祖先路径调整平衡因子

		//最多调整到根
		while (parent) {
			if (parent->_left == cur) {
				--parent->_bf;
			}
			else {
				++parent->_bf;
			}

			//说明该树的高度不变无需继续往上调整
			if (parent->_bf == 0) {
				break;
			}
			//该树的高度发生了变化，需要往上继续调整
			else if (parent->_bf == 1 || parent->_bf == -1) {
				cur = parent;
				parent = parent->_parent;
			}
			//此时该树高度失衡，需要进行旋转
			else if (parent->_bf == 2 || parent->_bf == -2) {
				//分别对几种旋转的情况进行判断

				//右边高需要左单旋
				if (parent->_bf == 2 && cur->_bf == 1) {
					rotateLeft(parent);
				}
				//左边高需要右单旋
				else if (parent->_bf == -2 && cur->_bf == -1) {
					rotateRight(parent);
				}
				//右左双旋
				else if (parent->_bf == 2 && cur->_bf == -1) {
					rotatRightLeft(parent);
				}
				//左右双旋
				else if (parent->_bf == -2 && cur->_bf == 1) {
					rotatLeftRight(parent);
				}
				else {
					assert(false);
				}
				break;
			}
			else {
				assert(false);
			}
		}
		return true;
	}
	void getSingleTreeHeight() {
		_getSingleTreeHeight(_root);
	}
	
private:
	void _getSingleTreeHeight(Node* root) {
		if (root) {
			printf("树%d的高度为：%d, 左子树为%d，右子树为%d\n\n",  
				root->_kv.first, getHeight(root), getHeight(root->_left), getHeight(root->_right));
			_getSingleTreeHeight(root->_left);
			_getSingleTreeHeight(root->_right);
		}
	}
	int getHeight(Node* root) {
		if (!root) {
			return 0;
		}
		int leftH = getHeight(root->_left);
		int rightH = getHeight(root->_right);
		return max(leftH, rightH) + 1;
	}
	void rotateLeft(Node* parent) {
		//对于左单旋只与三个结点有关
		//parent、cur(parent->_right)和cur->left
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		//cur一定不为空而cur->left是有可能为空的
		//因此需要特殊判断
		if (curleft) {
			//指向新parent
			curleft->_parent = parent;
		}
		//核心操作
		parent->_right = curleft;
		cur->_left = parent;	

		//先保存parent的父节点后续会用到
		//然后修改对应父节点的指向
		Node* oldparent = parent->_parent; 
		parent->_parent = cur;
		cur->_parent = oldparent;

		//parent可能是根节点也可能是一颗子树
		//若是根节点那么oldparent则为空
		//cur为新的根
		if (!oldparent) {
			_root = cur;
		}
		//否则判断parent结点是oldparent的哪颗子树
		//让其指向新的孩子cur
		else {
			if (oldparent->_left == parent) {
				oldparent->_left = cur;
			}
			else {
				oldparent->_right = cur;
			}
		}
		//旋转完毕后与插入之前(子)树的高度是不变的，同时还填上了矮的那颗子树
		//因此要修改cur和parent的平衡因子为0
		cur->_bf = parent->_bf = 0;
	}

	void rotateRight(Node* parent) {
		//右单旋的逻辑与左单旋非常相似
		// 
		//同样只与三个结点有关
		//parent、cur(parent->_left)和cur->_right
		Node* cur = parent->_left;
		Node* curright = cur->_right;
		if (curright) {
			curright->_parent = parent;
		}
		parent->_left = curright;
		cur->_right = parent;

		Node* oldparent = parent->_parent;
		parent->_parent = cur;
		cur->_parent = oldparent;

		if (!oldparent) {
			_root = cur;
		}
		else {
			if (oldparent->_left == parent) {
				oldparent->_left = cur;
			}
			else {
				oldparent->_right = cur;
			}
		}

		cur->_bf = parent->_bf = 0;
	}

	//右左双旋
	void rotatRightLeft(Node* parent) {
		//先保存关键结点的平衡因子
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		int bf = curleft->_bf;

		//复用单旋
		rotateRight(cur);
		rotateLeft(parent);

		//旋转后根据情况更新对应的平衡因子
		//自己就是新增
		if (bf == 0) {
			parent->_bf = cur->_bf = curleft->_bf = 0;
		}
		//在左边插入
		else if (bf == -1) {
			parent->_bf = curleft->_bf = 0;
			cur->_bf = 1;
		}
		//右边插入
		else if (bf == 1) {
			cur->_bf = curleft->_bf = 0;
			parent->_bf = -1;
		}
		else {
			assert(false);
		}
	}

	//左右双旋
	void rotatLeftRight(Node* parent) {

		Node* cur = parent->_left;
		Node* curright = cur->_right;
		int bf = curright->_bf;

		rotateLeft(cur);
		rotateRight(parent);

		if (bf == 0) {
			parent->_bf = cur->_bf = curright->_bf = 0;
		}
		//在左边插入
		else if (bf == -1) {
			cur->_bf = curright->_bf = 0;	 
			parent->_bf = 1;
		}
		//右边插入
		else if (bf == 1) {
			parent->_bf = curright->_bf = 0;
			cur->_bf = -1;
		}
		else {
			assert(false);
		}
	}
	Node* _root = nullptr;
};