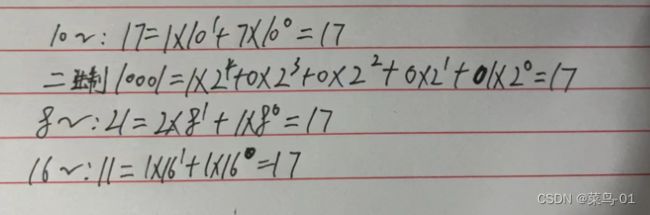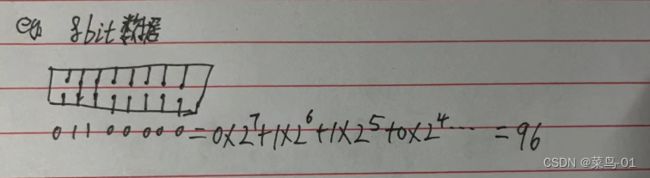单片机与进制数

目录

一:数字系统的由来

 A:二进制

1: 基础概念

2: 二进制运算

3:二进制的计算

 B:八进制

1:基础概念

C:16进制表

四:单片机中的进制数

---

一:数字系统的由来

1:远古时代:结绳计数

2:非位置化数字系统: 罗马数字

非位置化数字系统:  一个符号在不同的位置只会表达同样的意思, 不像位置化数字系统同样的一个符号表达不同的意思,  比如:在非位置化数字系统中ⅤⅤⅤ表达的是:5+5+5=15,表达出的数字直接就是他们相加相减的结果,所以非位置化数字系在生活中不怎么使用.

3:位置化数字系统: 二进制 | 八进制 |  十进制  |   十六进制

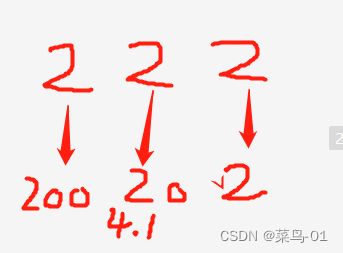
位置化数字系统:  一个符号在不同的位置表达不同的意思. 比如:我们人类使用的是十进制位置化数字系统222表达的是:如图4.1 而不是:2+2+2=6

 A:二进制

1: 基础概念

在计算机中只有0和1,断路和通路,满2进1。我们生活中使用的十进制是满十进1.  

• 二进制对应两种状态，广泛应用于电子科学。比如可以对应现实世界的灯的开关，0代表开灯，1代表灭灯，等等。

• 在计算机中，当电流流过时，为闭合状态，表示true（1），当没有电流流过时，为断开状态，表示false（0）。

2: 二进制运算

二进制的前缀围殴ob

加法：0+0=0，0+1=1，1+0=1，1+1=10 (满2进1)
减法：0-0=0，1-0=1，1-1=0，0-1=1(产生错位)
乘法： 0×0=0，1×0=0，0×1=0，1×1=1
二进制除法有两种情况(除数只能为1)：0÷1=0，1÷1=1

3:二进制的计算

（1）：基本运算

二进制采用的是位置计数法，其位权是以2为底的幂。对于有n位整数，m位小数的二进制数据用加权系数展开式表示，可写为

 

（2）：逻辑运算

与算符（&）：对于两个二进制数的与运算，只有当他们同一位的数字同为1时才为1，否则取0。相当于数学与的同真为真。（遇0则0）----在c语言中一般是为了清零使用-----清位操作

1&1=1，1&0=0，0&1=0，0&0=0；

 00110011 & 00000101 = 00000001

或运数（|）： 对于两个二进制数的或运算，一位任意一方的数字为1就取1，当同一位双方都为0时才取0。相当于数学的同假为假。（遇1则1）----在c语言中一般是为了置1使用----置位操作

10100 | 11101 =11101

取反运数（~,!）：对于二进制来说只有0和1，所以~0=1，  ~1=0

~10100=01011

异或运数（^,⊕）：对于两个二进制数的异或运算，一位的双方都同为0或者同为1则该位取0，不同取1。（不进位加(相同为0，相异为1)）---->必须不同,否则就没有

0 ^ 0 = 0、0 ^ 1 = 1、1 ^ 0 = 1、1 ^ 1 = 1

10100  ^ 11010 =01110

左移（<<）:左移运算符是一个计算机用语。用来将一个数的各二进制位全部左移若干位，移动的位数由右操作数指定，右操作数必须是非负值，其右边空出的位用0填补，高位左移溢出则舍弃该高位。

计算规则：将二进制数向左移动，右边补0。
0011（3）<<1=0110

结论：对于高位没有溢出的二进制数来说，左移n位相当于原数乘以2^n。

右移(>>) : 

清位操作和置位操作

 B:八进制

1:基础概念

八进制，基数有8位，数码由0、1、2、3、4、5、6、7组成，计数规律逢八进一。八进制是Octal，简写为O

        由于二进制数据的基数较小，所以二进制数据的书写和阅读不方便，为此，在小型机中引入了八进制。 八进制的数和二进制数可以按位对应（八进制一位对应二进制三位），因此常应用在计算机语言中

C:16进制表

A---10  B--11 C--12  D--13  E--14  F-15

四:单片机中的进制数

        在计算机中只能识别二进制, 所以不管你使用那种语言开发都会被转化为机器码. 我们正常生活中使用的是10进制.

 A:相同一个数字在不同进制下的表示方法

17:    10进制---17

         二进制--10001

          8进制--21

         16进制--11

B:c语言中进制的表示

int a =96   ------10进制

int a=0140  ----8进制(0开头)

int a=ox60 ------16进制(0x开头)

C:3大进制数的表示

1:二进制  数据的表示使用多个晶体管表示, 晶体管只有2个状态 on:1  off:0

        使用二进制描述, 吻合硬件的状态

        我们可以看见使用二进制数字可以直观观察出吻合的程度, 但是由于二进制太过于长, 我们引进了8进制和16进制来表示2进制

2:8进制

        在8进制中三bit一组, 在8进制中使用1位表示了3bit,   8进制的取值范围 0~7

3:16进制

        在16进制中4bit一组, 在16进制中使用1位表示了6bit,   16进制的取值范围 0~15

C:进制中的转(2/8/16进制的相互转化)

重要的二进制权重------8 4 2 1