前言
例说运算
圆锥曲线中的定值定点问题的运算往往少不了以下的过程。
将直线\(y=kx+2\)代入圆锥曲线\(\cfrac{x^2}{4}+\cfrac{y^2}{3}=1\)的代入运算过程,可以如下简化:
先将圆锥曲线整理为\(3x^2+4y^2-12=0\),然后这样在演草纸上书写,注意对齐书写,一次运算过
\(\left\{\begin{array}{l}{3x^2}\\{4(k^2x^2+4kx+4)}\\{\hspace{6em}-12}\end{array}\right.\)
一次就可以整理为\((4k^2+3)x^2+16kx+4=0\);
定点问题
- 动直线\(l\)过定点问题
解法思路:设动直线方程(斜率存在)为\(y=kx+t\),由题设条件将\(t\)用\(k\)表示为\(t=km\),得到\(y=k(x+m)\)形式,故动直线过定点\((-m,0)\);
- 动曲线\(C\)过定点问题
解法思路:引入参变量建立曲线\(C\)的方程,再根据其对参变量恒成立,令其系数等于零,得出定点。
典例剖析
例1【必会例题】\(A\)、\(B\)是抛物线\(y^2=2px(p>0)\)上的两点,且\(OA\perp OB\);
设\(A(x_1,y_1)\)、\(B(x_2,y_2)\),中点\(P(x_0,y_0)\)
(1)求\(A\)、\(B\)两点的横坐标之积和纵坐标之积;
分析:\(k_{OA}=\cfrac{y_1}{x_1}\),\(k_{OB}=\cfrac{y_2}{x_2}\),
由于\(OA\perp OB\),则有\(k_{OA}\cdot k_{OB}=-1\),则\(x_1x_2+y_1y_2=0\),
又由于\(y_1^2=2px_1\),\(y_2^2=2px_2\),则有\(\cfrac{y_1^2}{2p}\cdot \cfrac{y_2^2}{2p}+y_1y_2=0\),
由于\(y_1\neq 0\),\(y_2\neq 0\),故得到\(y_1y_2=-4p^2\),\(x_1x_2=4p^2\);
(2)求证:直线\(AB\)恒过定点;
分析:由于\(y_1^2=2px_1\),\(y_2^2=2px_2\),
所以\((y_1-y_2)(y_1+y_2)=2p(x_1-x_2)\),
所以当\(x_1\neq x_2\)时,\(\cfrac{y_1-y_2}{x_1-x_2}=\cfrac{2p}{y_1+y_2}\),即\(k_{AB}=\cfrac{2p}{y_1+y_2}\)
则直线\(AB:\) \(y-y_1=\cfrac{2p}{y_1+y_2}(x-x_1)\),即\(y=\cfrac{2px}{y_1+y_2}+y_1-\cfrac{2px_1}{y_1+y_2}\)
所以\(y=\cfrac{2px}{y_1+y_2}+\cfrac{y_1^2-2px_1+y_1y_2}{y_1+y_2}\)
由于\(y_1^2=2px_1\),\(y_1y_2=-4p^2\),
所以\(y=\cfrac{2px}{y_1+y_2}+\cfrac{-4p^2}{y_1+y_2}\),整理为\(y=\cfrac{2p}{y_1+y_2}(x-2p)\),
所以直线\(AB\)过定点\((2p,0)\),设\(M(2p,0)\),
当\(x_1=x_2\)时,可知\(AB\)方程为\(x=2p\),过点\(M(2p,0)\),
综上可知,直线\(AB\)恒过定点\(M(2p,0)\)。
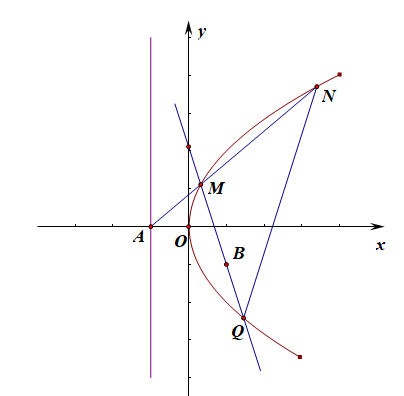
例2【衡水金卷,直线过定点类型】如图所示,已知点\(A(-1,0)\)是抛物线的准线与\(x\)轴的交点,过点\(A\)的直线与抛物线交于点\(M,N\)两点,过点\(M\)的直线交抛物线于另一个点\(Q\),且直线\(MQ\)过点\(B(1,-1)\).
(1).求抛物线的方程。
分析:由题目图形可知,\(\cfrac{p}{2}=1\),则\(p=2\),
故顶点在坐标原点,开口向右的抛物线的方程为\(y^2=2px\),即\(y^2=4x\)。
(2).求证:直线\(QN\)过定点。
分析:如果直线过定点\((m,n)\),则直线的表达式必然应该能化为:\(y-n=k(x-m)\)类型。
设点\(M(4t^2,4t)\),点\(N(4t_1^2,4t_1)\),点\(Q(4t_2^2,4t_2)\),
则由题目易知直线\(MN\)的斜率存在,且\(k_{MN}=\cfrac{4t-4t_1}{4t^2-4t_1^2}=\cfrac{1}{t+t_1}\),
从而直线\(MN\)的方程是\(y=\cfrac{1}{t+t_1}(x-4t^2)+4t\),
即直线\(MN\)的方程是\(x-(t+t_1)y+4tt_1=0\)。同理可知[类比求解可得],
直线\(MQ\)的方程\(x-(t+t_2)y+4tt_2=0\),
直线\(NQ\)的方程\(x-(t_1+t_2)y+4t_1t_2=0\),
又点\(A\)在直线\(MN\)上,从而有\(4tt_1=1\),即\(t=\cfrac{1}{4t_1}\);
点\(B\)在直线\(MQ\)上,从而有\(1+(t+t_2)+4tt_2=0\),
即\(1+(\cfrac{1}{4t_1}+t_2)+4\times \cfrac{1}{4t_1}t_2=0\),
化简得到\(4t_1t_2=-4(t_1+t_2)-1\),
代入\(NQ\)的方程,得到\(x-(t_1+t_2)y-4(t_1+t_2)-1=0\),
即\(y+4=\cfrac{1}{t_1+t_2}(x-1)\),故直线\(NQ\)经过定点\((1,-4)\)。
抛物线\(y^2=4x\)上的任意点的坐标的设法一般是\((x,y)\),本题采用\((4t^2,4t)\),是抛物线的参数方程的一种。
注意直线过定点的[题眼]:\(y-y_0=g(k)(x-x_0)\),则直线恒过定点\((x_0,y_0)\),其中\(g(k)\)表示关于参数\(k\)的表达式,可能简单也可能复杂。
延伸阅读:直线或函数恒过定点;
例3【定点问题】【2019届高三理科三轮模拟训练题第7套第20题】设抛物线\(C:x^2=2py(0
(1)求抛物线\(C\)的标准方程;
分析:由题意可得,\(F(0,\cfrac{p}{2})\),设\(P(x_0,y_0)\),由\(PF\)的中点坐标为\((2,\cfrac{5}{2})\),
得到\(0+x_0=2\times 2\)且\(\cfrac{p}{2}+y_0=2\times \cfrac{5}{2}\),所以\(x_0=4\),\(y_0=5-\cfrac{p}{2}\),
又由于\(P(x_0,y_0)\)在抛物线\(x^2=2py\)上,则有\(16=2p(5-\cfrac{p}{2})\),
即\(p^2-10p+16=0\),解得\(p=2\)或\(p=8\)(舍去),
故抛物线\(C\)的方程为\(x^2=4y\).
(2)若动直线\(l\)过点\(A(0,2)\),且与抛物线\(C\)交于\(M\)、\(N\)两点,点\(Q\)与点\(M\)关于\(y\)轴对称(点\(Q\)与点\(N\)不重合),求证:直线\(QN\)恒过定点。
分析:由题意可知,直线\(l\)的斜率存在,设直线\(l:y=kx+2\),\(M(x_1,y_1)\),\(N(x_2,y_2)\),则\(Q(-x_1,y_1)\),
联立\(\left\{\begin{array}{l}{x^2=4y}\\{y=kx+2,}\end{array}\right.\) 消去\(y\)得到,\(x^2-4kx-8=0\),
显然\(\Delta >0\),由韦达定理可知,\(x_1+x_2=4k\),\(x_1x_2=-8\),
由于\(k_{QN}=\cfrac{y_2-y_1}{x_2-(-x_1)}=\cfrac{\frac{x_2^2}{4}-\frac{x_1^2}{4}}{x_2+x_1}\)\(=\cfrac{x_2-x_1}{4}\),
所以直线\(QN\)的方程为\(y-y_1=\cfrac{x_2-x_1}{4}(x+x_1)\),
即\(y=y_1+\cfrac{x_2-x_1}{4}(x+x_1)=\cfrac{x_2-x_1}{4}x+\cfrac{x_1(x_2-x_1)}{4}+\cfrac{x_1^2}{4}\)\(=\cfrac{x_2-x_1}{4}x+\cfrac{x_1x_2}{4}\)
又由于\(x_1x_2=-8\),代入上式得到,\(y=\cfrac{x_2-x_1}{4}x-2\),
故直线\(QN\)的方程为\(y=\cfrac{x_2-x_1}{4}x-2\),即直线\(QN\)恒过定点\((0,-2)\)。
例4【恒过定点问题】【2019届高三理科寒假模拟试题1第20题】已知椭圆\(C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)的离心率为\(\cfrac{1}{2}\),且过点\(P(2,3)\),
(1)求椭圆\(C\)的标准方程;
分析:由于离心率\(e=\cfrac{1}{2}\),故有\(a:b=4:3\),设椭圆\(C\)的方程为\(\cfrac{x^2}{4}+\cfrac{y^2}{3}=t\),
又由于点\(P(2,3)\)在椭圆上,则有\(1+3=t\),即\(t=4\),
故椭圆\(C\)的标准方程为\(\cfrac{x^2}{16}+\cfrac{y^2}{12}=1\);
(2)过点\(P\)作两条直线\(l_1\),\(l_2\),与椭圆\(C\)分别交于\(M\),\(N\)(点\(M\),\(N\)与点\(P\)不重合),若\(l_1\),\(l_2\)的斜率之和为\(-1\),求证:直线\(MN\)恒过定点;
证明:设直线\(MN\)的方程为\(y=kx+b\),简单分析可知,当\(k\)不存在时,不满足要求;
联立\(\left\{\begin{array}{l}{\cfrac{x^2}{16}+\cfrac{y^2}{12}=1}\\{y=kx+b,}\end{array}\right.\) 消去\(y\)整理得到,\((4k^2+3)x^2+8kbx+4b^2-48=0\),
设点\(M(x_1,y_1)\),\(N(x_2,y_2)\),则有\(x_1+x_2=-\cfrac{8kb}{4k^2+3}\),\(x_1x_2=\cfrac{4b^2-48}{4k^2+3}\)
设直线\(PM\),\(PN\)的斜率分别为\(k_1\),\(k_2\),则\(k_1+k_2=\cfrac{kx_1+b-3}{x_1-2}+\cfrac{kx_2+b-3}{x_2-2}=-1\),
整理得到\((2k+1)x_1x_2+(b-2k-5)(x_1+x_2)+16-4b=0\),将\(x_1+x_2\)和\(x_1x_2\)代入整理,
即\((2k+b-3)(8k+b)=0\),解得\(b=-2k+3\)或\(b=-8k\);
当\(b=-2k+3\)时,直线\(MN:y=kx-2k+3=k(x-2)+3\)过点\(P(2,3)\),不合题意,舍去;
当\(b=-8k\)时,直线\(MN:y=kx-8k=k(x-8)+0\)过点\((8,0)\);
综上所述,直线\(MN\)恒过定点\((8,0)\).
例4【定值问题】已知离心率为\(\cfrac{1}{2}\)的椭圆\(C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)的右焦点为\(F\),且\(C\)过点\((1,-\frac{3}{2})\),
(1)求椭圆\(C\)的标准方程;
分析:由题可知,\(\left\{\begin{array}{l}{\frac{1}{a^2}+\frac{9}{4b^2}=1}\\{a^2=b^2+c^2}\\{\frac{c}{a}=\frac{1}{2}}\end{array}\right.\)
解得\(a=2\),\(b=\sqrt{3}\),故椭圆\(C\)的标准方程为\(\cfrac{x^2}{4}+\cfrac{y^2}{3}=1\).
(2)若不与\(x\)轴垂直的直线\(l\)与\(C\)交于\(M\),\(N\)两点(点\(M\),\(N\)均在\(y\)轴右侧,且\(M\),\(N\),\(F\)不共线),坐标原点\(O\)到直线\(l\)的距离为\(\sqrt{3}\),求\(\triangle MNF\)的周长.[或证明:\(\triangle MNF\)的周长为定值]
分析:由题目易知,直线\(l\)的斜率存在且不为零,
设其方程为\(y=kx+m(k\neq 0)\),\(M(x_1,y_1)\),\(N(x_2,y_2)\),
由于坐标原点\(O\)到直线\(l\)的距离为\(\sqrt{3}\),则有\(\cfrac{|m|}{\sqrt{1+k^2}}=\sqrt{3}\),即\(m^2=3(1+k^2)\),
由\(\left\{\begin{array}{l}{y=kx+m}\\{\cfrac{x^2}{4}+\cfrac{y^2}{3}=1,}\end{array}\right.\) 得到\((3+4k^2)x^2+8kmx+4m^2-12=0\),
整理为\((3+4k^2)x^2+8kmx+12k^2=0\),由韦达定理得到
\(x_1+x_2=-\cfrac{8km}{3+4k^2}\),\(x_1x_2=\cfrac{12k^2}{3+4k^2}\),
故\(|MN|=\sqrt{1+k^2}|x_1-x_2|=\sqrt{1+k^2}\sqrt{(x_1+x_2)^2-4x_1x_2}\) \(=\sqrt{1+k^2}\sqrt{(-\cfrac{8km}{3+4k^2})^2-4\times \cfrac{12k^2}{3+4k^2}}\) \(=\cfrac{4|m||k|}{3+4k^2}\)
因为\(2>x_1>0\),\(2>x_2>0\),由\(x_1+x_2>0\),所以\(mk<0\),
故\(|MN|=-\cfrac{4mk}{3+4k^2}\),
则\(|MF|^2=(x_1-1)^2+y_1^2=(\cfrac{1}{2}x_1-2)^2\),则\(|MF|=2-\cfrac{1}{2}x_1\),
同理得到,\(|NF|=2-\cfrac{1}{2}x_2\),
故\(|MF|+|NF|=4-\cfrac{1}{2}(x_1+x_2)=4+\cfrac{4km}{3+4k^2}\),
所以\(|MF|+|NF|+|MN|=4\),即\(\triangle MNF\)的周长为\(4\).
例5【定值问题】【2019届高三理科数学三轮模拟训练】已知直线\(l:y=kx+1\)与曲线\(C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>0,b>0)\)交于不同的两点,\(O\)为坐标原点,
(1)若\(k=1\),\(|OA|=|OB|\),求证:曲线\(C\)是一个圆;
证法1:设直线\(l\)和曲线的交点为\(A(x_1,y_1)\),\(B(x_2,y_2)\),
由于\(|OA|=|OB|\),则有\(\sqrt{x_1^2+y_1^2}=\sqrt{x_2^2+y_2^2}\),即\(x_1^2+y_1^2=x_2^2+y_2^2\)
即\(x_1^2-x_2^2=y_2^2-y_1^2\),又由于点\(A\),\(B\)在曲线\(C\)上,
则有\(\cfrac{x_1^2}{a^2}+\cfrac{y_1^2}{b^2}=1\),\(\cfrac{x_2^2}{a^2}+\cfrac{y_2^2}{b^2}=1\),
两式相减得到,\(x_1^2-x_2^2=\cfrac{a^2}{b^2}(y_2^2-y_1^2)\),
故\(\cfrac{a^2}{b^2}=1\),即\(a^2=b^2\),即曲线\(C\)是一个圆;
证法2:设直线\(l\)和曲线的交点为\(A(x_1,y_1)\),\(B(x_2,y_2)\),则\(x_1\neq x_2\),
由于\(|OA|=|OB|\),则有\(\sqrt{x_1^2+y_1^2}=\sqrt{x_2^2+y_2^2}\),即\(x_1^2+(x_1+1)^2=x_2^2+(x_2+1)^2\)
整理为\(2(x_1-x_2)(x_1+x_2+1)=0\),所以\(x_1+x_2=-1\),
由\(\left\{\begin{array}{l}{y=x+1}\\{\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1}\end{array}\right.\) 得到\((a^2+b^2)x^2+2a^2x+a^2(1-b^2)=0\),
\(\Delta\geqslant 0\),\(x_1+x_2=\cfrac{-2a^2}{a^2+b^2}\),所以\(\cfrac{-2a^2}{a^2+b^2}=-1\),
故\(a^2=b^2\),即曲线\(C\)是一个圆;
(2)若曲线\(C\)过\((0,2)\),\((1,0)\),是否存在一个定点\(Q\),使得\(\overrightarrow{QA}\cdot \overrightarrow{QB}\)为定值?若存在,求出定点\(Q\)和定值;若不存在,请说明理由。
分析:由题意得,椭圆\(C\)的方程为\(\cfrac{y^2}{4}+x^2=1\),假设存在点\(Q(x_0,y_0)\),设交点为\(A(x_1,y_1)\),\(B(x_2,y_2)\),
由\(\left\{\begin{array}{l}{y=kx+1}\\{x^2+\cfrac{y^2}{4}=1}\end{array}\right.\) 得到\((k^2+4)x^2+2kx-3=0\),
\(x_1+x_2=\cfrac{-2k}{k^2+4}\),\(x_1x_2=\cfrac{-3}{k^2+4}\),
由于直线\(l:y=kx+1\)恒过椭圆内定点\((1,0)\),故\(\Delta >0\)恒成立,
\(\overrightarrow{QA}\cdot \overrightarrow{QB}=(x_1-x_0,y_1-y_0)\cdot (x_2-x_0,y_2-y_0)\)\(=(x_1-x_0)(x_2-x_0)+(y_1-y_0)(y_2-y_0)\)
\(=x_1x_2-x_0(x_1+x_2)+x_0^2+(kx_1+1-y_0)(kx_2+1-y_0)\)\(=(1+k^2)x_1x_2+[k(1-y_0)-x_0](x_1+x_2)+x_0^2+(1-y_0)^2\)
\(=(1+k^2)\cfrac{-3}{k^2+4}+[k(1-y_0)-x_0]\cfrac{-2k}{k^2+4}+x_0^2+(1-y_0)^2\)\(=\cfrac{-3(1+k^2)-2[k(1-y_0)-x_0]k}{k^2+4}+x_0^2+(1-y_0)^2\)
\(=\cfrac{(2y_0-5)k^2+2x_0k-3}{k^2+4}+x_0^2+(1-y_0)^2\)
当\(\left\{\begin{array}{l}{x_0=0}\\{\cfrac{2y_0-5}{1}=\cfrac{-3}{4}}\end{array}\right.\),即\(x_0=0\),\(y_0=\cfrac{17}{8}\)时,\(\overrightarrow{QA}\cdot \overrightarrow{QB}=-\cfrac{3}{4}+(\cfrac{9}{8})^2=\cfrac{33}{64}\),
故存在定点\((0,\cfrac{17}{8})\),不论\(k\)为何值,都有\(\overrightarrow{QA}\cdot \overrightarrow{QB}=\cfrac{33}{64}\)为定值。
定值破解
由于这类问题的求解常常要用到韦达定理\(x_1+x_2\)和\(x_1x_2\)的值,故定值问题常常考查线段长度,三角形或四边形的周长,三角形或四边形的面积,向量内积等可以用上\(x_1+x_2\)和\(x_1x_2\)值的数学素材;
定值问题的破解题眼可能有以下情形:
①形如\(\cfrac{2k^2}{4+k^2}+\cfrac{8}{4+k^2}+1=\cfrac{2(k^2+4)}{4+k^2}+1=2+1=3\)为定值;
②加减消参法,和式中不含有参数,如\(3+\cfrac{2ak}{4+k^2}+1-\cfrac{2ak}{4+k^2}=4\),故为定值;比如上例;
③相乘消参法,积式中不含有参数,如\(\cfrac{2}{2k^2+3k}\cdot \cfrac{2k^2+3k}{8}=\cfrac{1}{4}\),故为定值;
④分式中对应项系数成比例消参,分式的值为定值;借用下例理解:
引例1,如设\(x\)轴上的一个动点\(P(x_0,0)\),某运算结果为\(\overrightarrow{PA}\cdot \overrightarrow{PB}=\cfrac{(8x_0-5)k^2-12}{3+4k^2}+x_0^2\),
要使得\(\overrightarrow{PA}\cdot \overrightarrow{PB}\)与\(k\)的取值无关,只需要\(\cfrac{8x_0-5}{-12}=\cfrac{4}{3}\),解得\(x_0=-\cfrac{11}{8}\),
所以在\(x\)轴上存在点\(P\),使得\(\overrightarrow{PA}\cdot \overrightarrow{PB}\)为定值,\(P\)的坐标为\((-\cfrac{11}{8},0)\),定值为\(-\cfrac{135}{64}\)。
引例2题目运算结果为\(\overrightarrow{QA}\cdot \overrightarrow{QB}=\cfrac{(2y_0-5)k^2+2x_0k-3}{k^2+4}+x_0^2+(1-y_0)^2\)
问:上述结果当\(x_0\)和\(y_0\)为何值时,运算结果与参数\(k\)无关,为定值?
当\(\left\{\begin{array}{l}{x_0=0}\\{\cfrac{2y_0-5}{1}=\cfrac{-3}{4}}\end{array}\right.\),即\(x_0=0\),\(y_0=\cfrac{17}{8}\)时,\(\overrightarrow{QA}\cdot \overrightarrow{QB}=-\cfrac{3}{4}+(\cfrac{9}{8})^2=\cfrac{33}{64}\),
故存在定点\((0,\cfrac{17}{8})\),不论\(k\)为何值,都有\(\overrightarrow{QA}\cdot \overrightarrow{QB}=\cfrac{33}{64}\)为定值。