密码学基础(四)——数据编解码
业务应用难题1:
隐私数据表现为五花八门的数据类型,不满足密码学协议中的特定的数据类型……
以密码学中的椭圆曲线(Elliptic Curve)加解密为例,介绍一种常见的数据映射方式。
一个比较简单的一类椭圆曲线:
y^2=x^3+ax+b(mod p)
其中满足公式成立的点(x,y)都在椭圆曲线上,椭圆曲线密码通过在限定的点集上定义相关的点运算,实现加解密功能。
问题是【如何将待加密的数据嵌入到椭圆曲线上,通过点运算来完成加密操作】?
即:
明文数据m——>特定点M(x,y)
需要对进来的数据按一定的规则处理,确保能放到椭圆曲线上。
于是,一种映射规则诞生——编解码
编码方式
Base64编码
概述:Base64编码是使用64个可打印字符来表示二进制数据的表示方法,通常用于存储和传输一些二进制数据,也就是将二进制数据文本化。
作用:
1. ASCII字符是多平台、多语言互通使用的,将非ASCII码转化为ASCII码;
2. 对二进制码进行文本化后的传输;
3. 前后台交互经常使用Base64编码,可以避免特殊字符传输错误。
编码规则
源文本——>ASCII编码——>二进制位——>按6位一组转换为64以内的数字——>Base64编码
注:不足6位,则自动补零。
业务应用难题2:
密码学协议中使用的核心算法对输入的数据长度往往有一定要求,而源自不同业务需求的隐私数据可长可短
数据过长——>数据分组
数据过短——>数据填充
加解密模式
ECB(Electronic Code Book,电子密码本)模式
分组规则:根据待加密数据的长度,进行平均分组。使用相同的密钥进行加密,最后串联在一起形成最终密文。
特点:相同密文,在相同的密钥下,密文是一样的。
因而使得密文数据在一定程度上暴露了关联性,并且依旧可读。
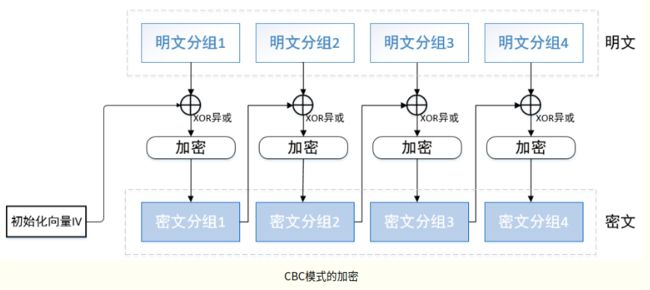
CBC(Cipher Blocking Chaining,密文分组链接)模式
分组规则:根据待加密数据的长度,进行平均分组。每个明文块先与前一个密文块进行异或后再进行密文组拼接。
特点:CBC模式解决了ECB模式的安全问题,但也带来了一定的性能问题。
其主要缺点在于每个密文块都依赖于前面的所有明文块,导致加密过程是产型的,无法并行化。
CTR(Counter,计数器)模式
分组规则:CTR模式的出现让分组加密更安全且并行化,通过递增一个加密计数器以产生连续的密钥流,使得分组密码变为流密码进行加密处理,安全性更高。每次加密时都会生成一个不同值(nonce)来作为计数器的初始值。
特点:CTR加密和解密过程均可以进行并行处理,使得在多处理器的硬件上实现高性能的海量隐私数据的并发处理成为了可能,这是目前最为推荐的数据分组模式。
数据填充
数据填充通常有两个作用一是按要求将数据补足到要就的块长度来满足加密算法的应用需求;二是通过增加填充数据来进一步提高密文的安全性。
PKCS7填充
填充规则:需要填充的部分都记录填充的总字节数,任何长度的原始数据,在最后一个数据块中,都要求进行数据填充。
PKCS7是当下各大加密算法都遵循的填充算法,且 OpenSSL 加密算法默认填充算法就是 PKCS7。
PKCS7Padding的填充方式为当数据长度不足数据块长度时,缺几位补几个几。
例如:对于AES128算法其数据块为16Byte(数据长度需要为16Byte的倍数),如果数据为“00112233445566778899AA”一共11个Byte,缺了5位,采用PKCS7方式填充之后的数据为“00112233445566778899AA0505050505”。
特别注意的一点是:如果是数据刚好满足数据块长度,也要在元数据后在按PKCS7规则填充一个数据块数据,这样做的目的是为了区分有效数据和补齐数据。仍以AES128为例:如果数据为”00112233445566778899AABBCCDDEEFF”一共16个符合数据块规则,采用PKCS7Padding方式填充之后的数据为“00112233445566778899AABBCCDDEEFF10101010101010101010101010101010”
总结
编解码在隐私保护领域用户用处很大,编解码过程中,以上提到的事数据映射、数据分组、数据填充,都是保证隐私数据安全的必要环节。
此外,在特定的合规要求下,实际业务系统还需要引入更多的数据预处理环节,如数据脱敏、数据认证等,使得数据在进入密码学协议前,尽早降低潜在的隐私风险。