AVL树 c语言版本 插入部分

目录

引入平衡树

为什么要变平衡

怎么判断是否需要变平衡

怎么变平衡

LL型失衡

RR型失衡

LR型失衡

RL型失衡

补充

左旋补充

右旋补充

Code

开辟一个新节点

 初始化

获取树的高度

左旋函数

更新树高

树高的求法

右旋转函数

插入

InsertNode()

更新树高

getbalance（）

根据balance判断是否失衡

RL型失衡​编辑如图(f-1）所示:

剩下的LR型失衡，RR型失衡，LL型失衡都同理，写为为如下这个样子:

测试函数

perOrder()

midOrder()

Find()

测试

代码托管

---

引入平衡树

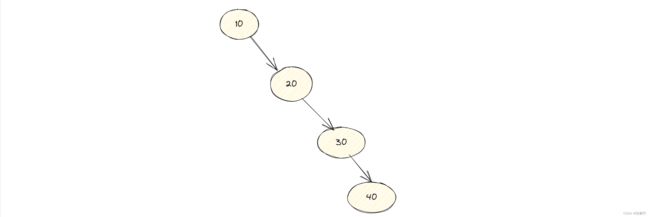
假设我们有两个节点：当我们插入第三个节点，就失衡了：此刻我们就要把它平衡一下。

为什么要变平衡

为什么说它失衡了呢，又为什么要把它变平衡？

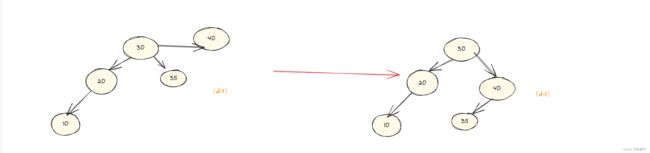
如图a，假设我们要查找30这个节点就要查3次才能找到

但是如果平衡之后(图b）就只需要2次就可以找到了，这样可以提高效率，这两个图不够明显，如果是100个节点的图就够明显了。

怎么判断是否需要变平衡

我们引入 平衡因子的概念

平衡因子 = 根节点的 左孩子高度 -  右孩子高度

当 平衡因子的绝对值 > 1 时，我们认为这个树是失衡的，需要变为平衡。

如图(c-1）：

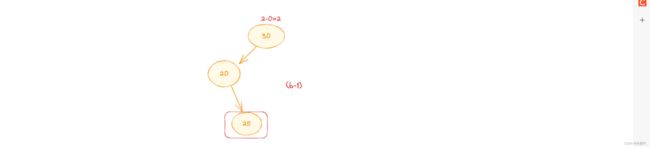
 根节点( 10 ) 的左孩子高度（0） - 右孩子高度（2）= 平衡因子 （-2）

| -2 | > 1，即该数树为失衡的树。

怎么变平衡

首先，假如有这样一个二叉搜索树：

LL型失衡

我们应该怎么平衡呢？

首先，因为根节点最小，所以把根节点变到2的右边，这也符合二叉搜索的特性，即：小了往左走

这个时候20就成了新的根节点，而原先的根节点10就成了现在根节点（20）的左孩子节点。

因此对于这种一边倒的二叉搜索树，并且是向左倒的：

 也就是要往左边分点节点，我们才能保持它的平衡，

对于LL型失衡，我们可以总结有如下 左旋定理:

RR型失衡

同理，有往左边倒的就有往右边倒的，如下图:

 因为40比30大的缘故，我们可以让40到30的右边去，这样就平衡了，并且符合二叉搜索树的特性，即:大了就往右边走:

此时30就是新节点，40就为30的右孩子。

这种往右边一边倒的失衡，我们称之为RR型失衡。

对此，我们可以总结如下右旋定理:

LR型失衡

因为root节点的左孩子的右节点造成的失衡就叫LR型失衡，如图 (b-1)：

因为是由于右节点造成的失衡，所以我们就让右节点到左节点去，可以用左旋定理：

变为图 （b-2）:

 图(b-2)我们看它的平衡因子，大于1，所以还要再变。

又因为图(b-2）是RR型失衡，所以套用  右旋定理：

变为图（b-3）:

此时平衡因子<1，是AVL树，因此不再变。

流程图：

RL型失衡

如图（a-1），因为root节点的右孩子的左节点造成的失衡就叫RL型失衡：

对于LR型失衡，因为是左节点造成的失衡，所以要先采用右旋定理把右节点变到左边去：

变为图（a-2）：

此时平衡因子为 -2 ，仍然不平衡还需要再变

此时因为向左倾斜，即要向左部分分点，这样才平衡要调用  左旋定理 ：

变为图 （a-3）：此时平衡因子 <1,即不用再变。

流程图:

因此，我们可以只有总结:

补充

左旋补充

有如下图：

 此时应该先左旋，然后再按二叉搜索树的特性再排

旧根节点10比  新根节点原先的左子树 19小，所以19应该排到10右边：

因此，左旋定理可以得到补充，如下:

右旋补充

有图（d-1）：此时应该先右旋，再按二叉搜索树特性排：

 因此，右旋定理可以得到如下补充:

Code

首先写一下树的结构

val left right是必须的，又新加了一个height，用来求平衡因子用:

typedef  struct Node
{
	int val;//数据域
	int height; //树高
	struct Node* left;
	struct Node* right;
}Node;

开辟一个新节点

Node* newnode = (Node*)malloc(sizeof(Node));

 初始化

node->val=val;
node->height = 1;
node->left = NULL;
node->right = NULL;

 开辟和初始化我们都封装起来:

Node* newnode(int val)
{
Node* node = (Node*)malloc(sizeof(Node));
node->val=val;
node->height = 1;  //只有一个节点时，树高为1
node->left = NULL;
node->right = NULL;

retur node;
}

获取树的高度

如果树高度为空，返回0

否则就把树的高度返回。

//获取树的高度
int getHeight(Node* node)
{
	if (node->height == NULL)
		return 0;
	else
		return node->height;
}

接下来写左旋函数，右旋函数

左旋函数

左旋函数先按左旋定理写:

int LeftRtate(Node* root)
{
	//新节点为旧节点的右子树
	Node* newroot = root->right;

	//T2时新根节点的左子树
	Node* T2 = newroot->left;

}

 开始旋转:

开始旋转:
	//旧根节点变为新根节点的左子树
	newroot->left=root;

	//如果新根节点原来有右子树，那么新根节点原来右子树变为旧节点的右子树
	root->right = T2;

更新树高

经过左旋之后root和newroot的高度都变了，我们需要更新一下。

怎么更改呢？首先需要先求树高。

树高的求法

拿图（b-1）举例:

 图(b-1)的树高为3，其中，左子树的树高为2，右子树的树高为0。

我们取左右子树最大的树高+1就是整个树的树高：

int max(int A,int B)
{
	if (A > B ? A : B);

}

int LeftRtate(Node* root)
{
	//新节点为旧节点的右子树
	Node* newroot = root->right;

	//T2时新根节点的左子树
	Node* T2 = newroot->left;

	//旧根节点变为新根节点的左子树
	newroot->left=root;

	//如果新根节点原来有右子树，那么新根节点原来右子树变为旧节点的右子树
	root->right = T2;

	//树高
 root->height = 1+max(getHeight(root->left),getHeight(root->right));
 newroot->height = 1+max(getHeight(newroot->left), getHeight(newroot->right));

 return newroot;//返回新根节点

右旋转函数

同样的道理，按照右旋定理就可以了：

Node* RightRatate(Node* root)
{
	//新根节点为原先旧节点的左子树
	Node* newroot = root->left;

	//新根节点的右子树
	Node* T2 = newroot->right;

	//开始旋转
	//旧根节点变为新根节点的右子树
	newroot->right = root;

	//3.如果新根节点原来有右子树，那么新根节点的右子树就会作为旧根节点的左子树
	root->left = T2;
	//树高
	root->height = 1 + max(getHeight(root->left), getHeight(root->right));
	newroot->height = 1 + max(getHeight(newroot->left), getHeight(newroot->right));

	return newroot;
}

接下来就是重头戏

插入

首先按照搜二叉的方式插入，

如果key值比当前节点值大就插在当前节点右边，否则就插在当前节点的左边。

插入完之后可能会造成失衡。

怎么判断失衡呢？根据平衡因子。

然后再去按照时哪种失衡，进行对应的调整。

欧克，一步一步来，首先插入

InsertNode()

//插入
Node* InsertNode(Node* node,int key)
{
	
	

}

如果当前节点为空，那么就调用我们的newnode()函数，malloc了一个节点并且对节点进行初始化

Node* InsertNode(Node* node,int key)
{
	
	if (node==NULL)return newnode(key);

}

如果key值比当前节点值大就插在当前节点右边，否则就插在当前节点的左边:

Node* InsertNode(Node* node,int key)
{
	if (node==NULL)return newnode(key);
    
	if (key > node->val)(node->left = InsertNode(node->right, key));
	if (key < node->val)(node->left = InsertNode(node->left, key));
	
}

接下来就是用平衡因子判断插入之后是否失衡了。

写一个求平衡因子的函数:

但是在此之前需要先更新一下树高，因为平衡因子是根据树高求出来的。

更新树高

树高的求法：左右子树树高最大的那一个+1。

Node* InsertNode(Node* node,int key)
{
	if (node==NULL)return newnode(key);
    
	if (key > node->val)(node->left = InsertNode(node->right, key));
	if (key < node->val)(node->left = InsertNode(node->left, key));
	
	//更新树高
	//因为root改变了，所以它俩的树高需要更新
	node->height = 1 + max(getHeight(node->left), getHeight(node->right));
}

getbalance（）

平衡因子的求法在刚开始就说过，就是左子树的树高-右子树的树高。

int getbalance(Node* node)
{
	return getHeight(node->left)- getHeight(node->right);

}

根据balance判断是否失衡

 拿RL型失衡举例:

RL型失衡如图(f-1）所示:

根节点的 balance（平衡因子) =-2   根节点的右子树的balance=1

此时为RL型失衡。

balance<-1 && getbalance(node->right) < 0

RL失衡了就按照我们之前写的那个平衡方法就平衡一下:

先右旋，再左旋

   node->right=RightRatate(node->right);  即node链接右边的节点，让要旋转的节点旋到右边
		return LeftRtate(node);

剩下的LR型失衡，RR型失衡，LL型失衡都同理，写为为如下这个样子:

if (balance< -1 && getbalance(node->right)>0)
	{
		//RL失衡
		//需要先右旋，再左旋
       node->right=RightRatate(node->right);
		return LeftRtate(node);
		
	}
	if (balance >1 && getbalance(node->left) <0)
	{
		//LR失衡
		//需要先左旋旋，再右旋
	
		node->left=LeftRtate(node->left);	
		return RightRatate(node);
	}
	if (balance<-1 && getbalance(node->right) < 0)
	{
		//RR型失衡
		//右旋
		return LeftRtate(node);
	}
	if (balance>1 && getbalance(node->right) >0)
	{
		//LL失衡
		//左旋
		return RightRatate(node);
	}

最后把根节点返回就可以了。

	return node;

至此，Insert()就全部写完了，总结为如下:

//插入
Node* InsertNode(Node* node,int key)
{
	if (node==NULL)return newnode(key);
    
	if (key > node->val)
	{
		node->right = InsertNode(node->right, key);
	}
	else if (key < node->val)
	{
		node->left = InsertNode(node->left, key);
	}
	else
	{
		return node;
	}
	
	//更新树高
	//因为root改变了，所以它俩的树高需要更新
	node->height = 1 + max(getHeight(node->left), getHeight(node->right));

	//根据balance判断是否失衡

	int balance = getbalance(node);

	if (balance< -1 && getbalance(node->right)>0)
	{
		//RL失衡
		//需要先右旋，再左旋
       node->right=RightRatate(node->right);
		return LeftRtate(node);
		
	}
	if (balance >1 && getbalance(node->left) <0)
	{
		//LR失衡
		//需要先左旋旋，再右旋
	
		node->left=LeftRtate(node->left);	
		return RightRatate(node);
	}
	if (balance<-1 && getbalance(node->right) < 0)
	{
		//RR型失衡
		//右旋
		return LeftRtate(node);
	}
	if (balance>1 && getbalance(node->right) >0)
	{
		//LL失衡
		//左旋
		return RightRatate(node);
	}

	return node;
}

然后我们来写测试函数

测试函数

我们可以用前序和后续就可以打印看看是否出错了，先写前序

perOrder()

void perOrder(Node* root)
{
	if (root == NULL)return;
	printf("%d ", root->val);
	perOrder(root->left);
	perOrder(root->right);

	
}

midOrder()

void midOrder(Node* root)
{
	if (root == NULL)return;
	midOrder(root->left);
	printf("%d ",root->val);
	midOrder(root->right);
	
}

Find()

find有三个参数

写一个根节点，把根节点赋值给当前节点，让当前节点去遍历。一个count参数统计查找次数。

key为要查找的值。

注意，count类型为int*而不是Int.

因为我们想让count的改变影响我们外面的实参值。

Node* Find(Node* root,int* count，int key)
{

}

如果要查找的值比当前节点小，就往左走，否则如果比当前节点大，就往右走，如果不大不小那就说明要找的就是当前节点，把当前节点return。

如果找了一圈都没有找到，即当前节点跌代到空节点都找不到，那就返回NULL。

注意不是返回false，因为我们的Find（）函数还要统计次数的功能，因此不是并没有给它一个bool类型。

Node* Find(Node* root,int* count,int key)
{
	Node* cur = root;
	while (cur)
	{
		if (key> cur->val)
		{
			cur = cur->right;
			(*count)++;
		}
		else if (key > cur->val)
		{
			cur = cur->left;
			(*count)++;
		}
		else
		{
			return cur;
		}
		
	}
	return NULL;
}

测试

void test()
{
	Node* root = NULL;
	root= InsertNode(root,  10);
	root = InsertNode(root, 20);
	root = InsertNode(root, 30);
	root = InsertNode(root, 40);
	root = InsertNode(root, 50);
	root = InsertNode(root, 60);
	root = InsertNode(root, 70);
	

	int count = 0;
	int key = 70;
	Node* result=Find(root, &count, key);
	printf("要找的值是:%d\n",key);
	printf("找了%d 次\n",count);

	printf("前序遍历:_______ _ __  _\n");
	perOrder(root);
	printf("\n中序遍历:_______ _ __  _\n");
	midOrder(root);
}

报错：这是因为我们应该判断node==NULL，而不该去判断node->height；

当node为空时，node->height就是空指针指向height就会报错。

改为如下图：运行:

我们根据前序和中序打印的结果，可以画出这样一个二叉树:

 这个二叉树是一个平衡二叉树，即AVL树，并且找7这个节点找3次就能找到。

而我们打印出来的要找两次是因为我们根节点那次没算，当cur=node也让count++就可以了。

代码托管

AVLTreeinsert.c ·