第 117 场 LeetCode 双周赛题解

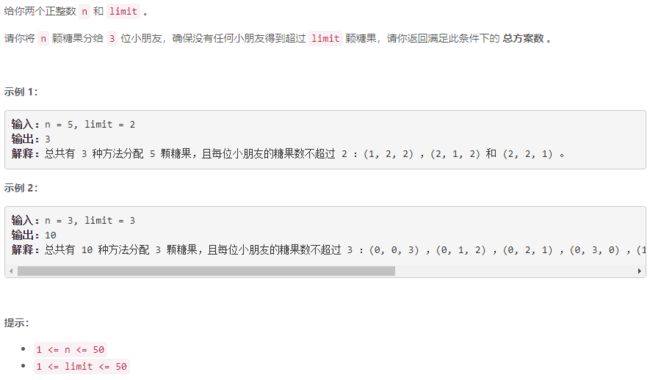
A 给小朋友们分糖果 I

动态规划：设 $p[k][i]$ 为将 $i$ 个糖果分给 $k$ 个小朋友的方案数，先求 $p[2][i]$ ，再求 $p[3][n]$

class Solution {
public:
    using ll = long long;

    int distributeCandies(int n, int limit) {
        ll p[4][n + 1];
        memset(p, 0, sizeof(p));

        for (int i = 0; i <= n; i++) {
            p[2][i] = min(limit, i) - max(0, i - limit) + 1;
        }
        ll res = 0;
        for (int i = 0; i <= limit && i <= n; i++)
            if (n - i <= 2 * limit)
                res += p[2][n - i];
        return res;
    }
};

---

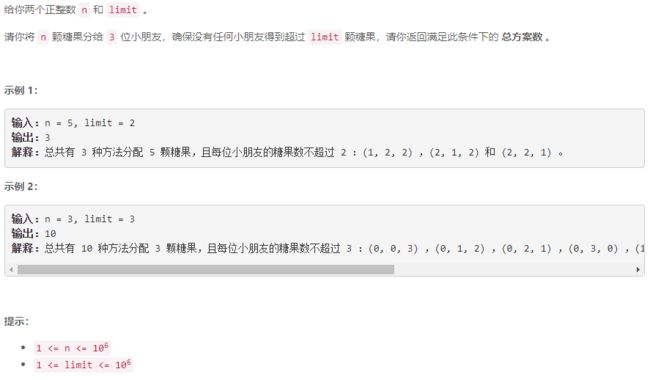
B 给小朋友们分糖果 II

同 $A$ …

class Solution {
public:
    using ll = long long;

    long long distributeCandies(int n, int limit) {
        ll p[4][n + 1];
        memset(p, 0, sizeof(p));

        for (int i = 0; i <= n; i++) {
            p[2][i] = min(limit, i) - max(0, i - limit) + 1;
        }
        ll res = 0;
        for (int i = 0; i <= limit && i <= n; i++)
            if (n - i <= 2 * limit)
                res += p[2][n - i];
        return res;
    }
};

---

C 重新排列后包含指定子字符串的字符串数目

动态规划：设 $p[i][cl][ct][ce]$ 为用 $i$ 个字符组成的 $l,t,e$ $3$ 种字符数分别为 $cl,ct,ce$ 个的字符串数目，$l$ 字符数 $>1$ 的字符串状态算在 $cl=1$ 的状态内，类似 $t$ 字符数 $>1$ 的字符串状态算在 $ct=1$ 的状态内，$e$ 字符数 $>2$ 的字符串状态算在 $ce=2$ 的状态内，答案即为 $p[n][1][1][2]$

class Solution {
public:
    using ll = long long;
    ll mod = 1e9 + 7;

    int stringCount(int n) {
        ll p[n + 1][2][2][3];
        memset(p, 0, sizeof(p));
        p[0][0][0][0] = 1;//空串
        for (int i = 1; i <= n; i++) {
            for (int l = 0; l < 2; l++) {
                for (int t = 0; t < 2; t++) {
                    for (int e = 0; e < 3; e++) {
                        p[i][l][t][e] = p[i - 1][l][t][e] * 23 % mod;//第i个字符为非l,e,t的字符
                        if (l) {//第i个字符为l
                            p[i][l][t][e] += (p[i - 1][l - 1][t][e] + p[i - 1][l][t][e]) % mod;
                            p[i][l][t][e] %= mod;
                        }
                        if (t) {//第i个字符为t
                            p[i][l][t][e] += (p[i - 1][l][t - 1][e] + p[i - 1][l][t][e]) % mod;
                            p[i][l][t][e] %= mod;
                        }
                        if (e) {//第i个字符为e
                            p[i][l][t][e] += p[i - 1][l][t][e - 1];
                            p[i][l][t][e] %= mod;
                            if (e == 2) {
                                p[i][l][t][e] += p[i - 1][l][t][e];
                                p[i][l][t][e] %= mod;
                            }
                        }
                    }
                }
            }
        }
        return (p[n][1][1][2] + mod) % mod;
    }
};

---

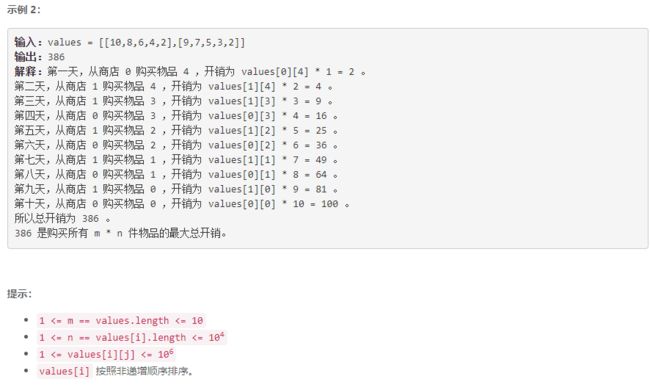
D 购买物品的最大开销

贪心 + 优先级队列：每次购买当前各商店最右商品价格最小的最右商品即可获得最大总开销，用优先级队列维护各商店最右商品价格最小值

class Solution {
public:
    using ll = long long;
    
    long long maxSpending(vector<vector<int>> &values) {
        int m = values.size(), n = values[0].size();
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> heap;//最小堆
        for (int i = 0; i < m; i++)
            heap.emplace(values[i][n - 1], i, n - 1);
        ll res = 0;
        for (int i = 1; i <= m * n; i++) {
            auto [v, r, c] = heap.top();
            heap.pop();
            res += 1LL * i * v;
            if (c)//该商店还有剩余商品
                heap.emplace(values[r][c - 1], r, c - 1);
        }
        return res;
    }
};