VSLAM(7):后端优化---滤波器方法和BA图优化
在视觉里程计完成每次的位姿估计后,可以实时地得到一个短时间内的轨迹和地图点,但是由于估计本身具有误差,这个误差会一直保持并不断累加。所以可以构建一个尺度和规模更大的优化问题,来计算一段长时间内的最有轨迹和地图。
一, 后端优化综述
SLAM问题可以由运动方程和观测方程描述,设从t=0到t=N这个时间段内,机器人经过了![]() 到的位姿点,观测到了这么多的特征点,那么有:
到的位姿点,观测到了这么多的特征点,那么有:
视觉前段往往在某一时刻会观测很多的特征点,所以实际中观测方程的数量会远远多于运动方程的数量;同时,机器人系统本身没有测量运动设备,可能不具备运动方程,这时候的优化问题就由很多个观测方程组成。
后端(backend)实现的是其实本质上是一个状态估计问题,从带噪声的估计数据(noisy data)中估计内在状态(inner state)。在前端的数据进来后,本身带有误差,而后端要处理的就是将这个误差最小化。如果我们考虑k时刻之前的所有状态关系,此时就可以使用非线性优化的方法在一定数据规模内构造非线性问题来求解最优解,这种方法称为批量式(Batch)。另一种方法称为渐进式(incremental),是基于马尔可夫性,假设当前时刻的状态只跟上一刻的状态有关。这类方法最具代表性的就是基于卡尔曼滤波器。
二,渐进式
2.1 线性系统与KF
当一个系统是线性系统,并且它的运动模型和观测模型符合高斯分布,那这时候就可以用卡尔曼滤波对状态进行最有估计。卡尔曼滤波的原理是基于贝叶斯公式和高斯分布相乘还是高斯分布的特性推导出来的,具体的推到公式网上很多。
2.2 非线性系统和EKF
当系统是一个非线性系统时,为了使卡尔曼滤波继续成立,可以利用一节泰勒展开来对系统做近似线性化,再对线性化后的系统使用卡尔曼滤波,得到最优估计。这种方法叫做扩展卡尔曼滤波,也称为EKF(extend Kalman Filter)。
2.3 其他滤波器方法
上溯两种最基础的滤波器方法都是基于噪声符合高斯分布的假设下,但是实际的噪声分布往往是各种模型甚至没有具体的模型。对于已知的噪声分布,往往可以使用粒子滤波的方法来对状态进行估计。粒子滤波器是假设噪声分布符合一定规律,这时候就可以按照这个噪声分布撒n个粒子来近似噪声的分布,同时每个粒子的权重与它与均值之间的距离成反比。每个周期对粒子权重进行更新,同时将权重过小的粒子剔除并撒进行新的粒子代替。具体的解释可以参考
除了粒子滤波,还有滑动窗口(sliding window filter)和MSCKF(multiple state Kalman)等基于滤波器的方法。
三,批量式
3.1 Bundle Adjustment
BA(Bundle Adjustment)是基于观测到的一定量的数据,书写多个关于位姿和路标的等式,利用非线性优化的方法求解最优值。相机的观测模型记作:
其中x为相机位姿的李代数,y为路标的三位坐标。而观测数据则是路标的像素坐标。设相机在![]() 处观测到了路标
处观测到了路标![]() ,那么整个BA优化的代价函数就可以定义为:
,那么整个BA优化的代价函数就可以定义为:
待优化的变量为:
就像之前介绍的优化方法,我们需要求解每次循环的增量来逼近最优值,目标函数就变成了:
其中代表整个代价函数在当前状态下对相机位姿的偏导数,而代表代价函数在当前状态下对路标点的偏导数。
求解优化增量,需要求解增量线性方程,对于G-N和L-M方法,有:
两种方法的区别就是H的定义不一样,一个是![]() ,另一个是。但是雅可比矩阵的定义是一样的,都是:
,另一个是。但是雅可比矩阵的定义是一样的,都是:![]()
但是因为需要同时优化位姿和路标,矩阵的维度往往会很大,对H的求导往往很复杂。
3.2 稀疏性和边缘化
考虑一个误差项![]() ,他表示机器人在第i个位姿下观测到了第j个路标,那么这个误差项就只跟这两项有关,其他项求偏导就为零,所以该误差的格式如下:
,他表示机器人在第i个位姿下观测到了第j个路标,那么这个误差项就只跟这两项有关,其他项求偏导就为零,所以该误差的格式如下:
这个误差项除了两处为非零块,其他均为零。这体现了该误差项和其他路标和轨迹无关的特性。假设使用高斯牛顿的方法求解非线性最优值,那么此时就有![]() ,根据雅可比矩阵的性质,我们可以将H进行分块:
,根据雅可比矩阵的性质,我们可以将H进行分块:
左上角是误差关于位姿的雅可比矩阵,右下角是关于路标点的。在遍历这个矩阵的时候,不管i和j怎么变,都是一个对角阵,只有在处非零;同样的![]() 也只在
也只在![]() 处非零。对于另外两个矩阵和,他们由具体的观测情况而定,如过每次观测都可以观测到很多的路标,那么他们就是稠密的,反之则是稀疏的。
处非零。对于另外两个矩阵和,他们由具体的观测情况而定,如过每次观测都可以观测到很多的路标,那么他们就是稠密的,反之则是稀疏的。
这里高博举了一个例子来更好的说明H的稀疏性。假设机器人经过2个位姿点,观测到了6个路标点。在位姿1处观测到了P1-4,而在位姿二处观测到了P3-6,这个场景的图结构如下图所示:
那么此时的我们需要优化的BA目标函数就是:
以 为例,这个误差函数代表了相机在位姿点1初观测到路标点1这个事件的误差,因为只跟路标点1和位姿点1有关,所以他的雅可比矩阵定义如下:
![]()
可以直观的看到这个雅可比矩阵中只有两个非零块,大小分别是2*6和2*3,用图来表示就是:
当我们把每个误差项都进行这样的操作后就得到一个8*8个矩阵块的雅可比矩阵,同时根据高斯牛顿法其对应的H矩阵也会有类似的结构:
在实际情况中,路标数量往往会远大于位姿点数量,这就导致右上角的维度远小于![]() 的,整个H的形状会像箭头一样,成为箭头形(Arrow-like)矩阵,如下图:
的,整个H的形状会像箭头一样,成为箭头形(Arrow-like)矩阵,如下图:
这样我们就可以这个性质来加速计算求解线性方程![]() ,加速手段又称为边缘化(Marginalization)或则叫做Schur消元(Schur trick)。将H矩阵按以下区域划分:
,加速手段又称为边缘化(Marginalization)或则叫做Schur消元(Schur trick)。将H矩阵按以下区域划分:
其中B和C是对角块矩阵,B的每个对角块的维度和位姿点维度一样,对角块个数和位姿点个数一样,C代表路标点,同理,每个块的维度为3*3,数量为路边点总数。对角块矩阵的求逆难度往往远小于一般矩阵的求逆难度,所以可以分开求逆。利用高斯消元可以将右上角的E消去,然后就可以先解第一行关于位姿的增量方程,把解出来的位姿增量![]() 代入到原方程求解路标增量。具体的计算过程如下:
代入到原方程求解路标增量。具体的计算过程如下:
整理得
将第一行提取出来得到
可以看到,这个方程需要求解,因为C是对角块矩阵这个性质,求解会容易很多。同时在求解出![]() 后,利用方程就可以求解出路标增量。这个过程称为Marginalization或则Schur消元。下图展示了一个上面线性方程系数矩阵S的实例,可以看出它并不是稀疏的:
后,利用方程就可以求解出路标增量。这个过程称为Marginalization或则Schur消元。下图展示了一个上面线性方程系数矩阵S的实例,可以看出它并不是稀疏的:
同时这个矩阵也是有一定意义的:它的非对角线上的非零矩阵块,表示了该处对应两个相机变量之间存在共视(co-visiblity)关系,即他们共同观测到某个路标点。反之为零则表示没有共同观测
从概率角度来解释边缘化,实际是把同时求解(![]() )变成了先求解
)变成了先求解![]() 再求解。相当是求解条件概率:
再求解。相当是求解条件概率:
3.3 鲁棒核函数
因为实际情况中往往存在误匹配的情况,导致加入一些本应该没有的边加入图优化中。这边的误差很大的时候往往会抹平其他正确变得影响,使得最终的优化结果与正确值偏差很大。因为上面对于优化函数定义为误差的平方(即二范数),这在误差比较大时会增长很快,为了解决这个问题,引入核函数来保证每条边的误差不会过大,导致最终结果偏差大。
把原先的优化函数从误差的二次方替换为一个其他函数。这个替换的函数需要增长没有那么快,同时保证自己的光滑性,使得整个优化过程更加鲁棒。这个函数成为鲁棒核函数(Robust Kernal)
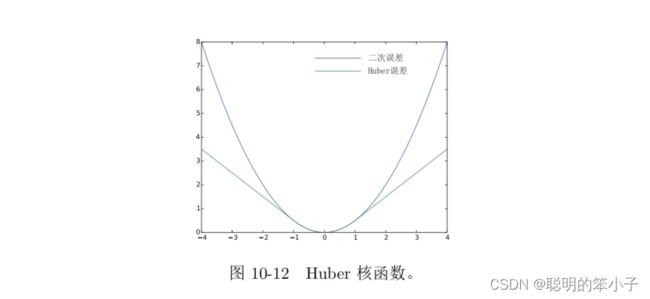
常见的鲁棒核函数由Huber核:
这个核函数表示的是当误差不超过阈值时候,还是按照二范数来定义,但是如果大于阈值,就由二次型转换为了一次型,限制了增长速度。同时Huber函数也是光滑的,便于求导。下图是Huber函数与二次函数的对比:
除了Huber核,还有Cauthy核,Tukey核,在g2o和ceres函数库中有定义。