第五章 CUDA获得GPU加速的关键
本章关注CUDA程序的性能,需要对主机代码和设备函数进行计时。
5.1 用CUDA事件计时
在C++中有多种方法对一段代码进行计时的方法,包括使用GCC和MSVC都有的clock()函数和与头文件
cudaEvent_t start,stop;
CHECK(cudaEventCreate(&start));
CHECK(cudaEventCreate(&stop));
CHECK(cudaEventRecord(start));
cudaEventQuery(start);
需要计时的代码块
CHECK(cudaEventRecord(stop));
CHECK(cudaEventSynchronize(stop));
float elapsed_time;
CHECK(cudaEventElapsedTime(&elapsed_time,start,stop));
printf("Time = %g ms.\n",elapsed_time);
CHECK(cudaEventDestroy(start));
CHECK(cudaEventDestroy(stop));
下面对该计时方式进行解释:
(1)第一行定义了两个CUDA事件(cudaEvent_t)的start和stop,并在定义之后使用cudaEventCreate()进行初始化。
(2)在第四行中使用定义和初始化(cudaEventCreate())好的事件start(cudaEvent_t)进行记录一个开始事件(cudaEventRecord()),其代表一个代码开始事件。
(3)第五行cudaEventQuery()对于TCC驱动模式的GPU来说可以省略,但对于WDDM驱动模式中的GPU必须保留。原因在于,处于WDDM驱动模式中的GPU中,一个CUDA流(CUDA Stream)中的操作(cudaEventCreate())并不是直接提交给GPU执行,而是先提交到一个软件队列,需要添加一条对该流的cudaEventQuery()操作(或cudaEventSyncronize()操作)来进行刷新队列,才能保证前面的cudaEventCreate()操作在GPU中执行。
(4)第七行中代表一个需要计时的代码块,可以使主机代码、也可以是设备代码、也可以式混合代码的调用。
(5)在第九行中stop事件(cudaEvent_t)传入cudaEventRecord()中并记录这是一个代表结束的事件。
(6)第十行的cudaEventSynchronize()是让主机等待事件stop被记录完毕。
(7)第11-13行调用cudaEventElapsedTime()计算start和stop之间的时间差(ms)并输出到屏幕。
(8)最后使用cudaEventDestroy()摧毁事件start和stop。
5.1.1 为C++程序计时
本章节程序add1cpu.cu程序是在博文第三章的程序add.cpp的基础上进行改写的,主要有以下三个部分的改动:
(1)即使该程序中没有使用核函数,但也将源程序的扩展名改为了.cu,这样就不用包含一些CUDA的头文件了,若用.cpp用nvcc编译时需要明确的增加一些头文件的包含,用g++编译时还要明确地链接一些CUDA库。
(2)在本章中用条件编译选项选择所用浮点数的精度。在程序开头部分有如下几行代码:
# ifdef USE_UP
typedef double real;
const real epsilon=1.0e-15;
#else
typedef float real:
const real epsilon=1.0e-6f;
#endif当宏USE_DP有定义时,程序中的real代表double,否则代表float,可以通过编译选项定义。
(3)用CUDA事件对该程序中的add()调用进行计时,并且重复了11次,并忽略第一次测得的时间,因为第一次计时,机器(GPU和CPU)都处于预热状态,测得的时间往往偏大。根据后十次计算的平均值。具体参照下面的程序。
#include
#include
#include
# ifdef USE_DP
typedef real double;
const real epsilon=1.0e-15;
#else
typedef real float;
const real epsilon=1.0e-6;
#endif
const int calcnumber=10;
const real epsilon=1e-15;
const real a=1.23;
const real b=2.34;
const real c=3.57;
void add(real *a,real *b,real *c,const int number)
{
for(int i=0;iepsilon)
{
throw i;
}
}
}
int main()
{
const int Number=1e10;
const int ByteNumber=Number*sizeof(int);
real *x=(double*)malloc(ByteNumber);
real *y=(double*)malloc(ByteNumber);
real *z=(double*)malloc(bytenumber);
for(int i=0;i 0)
{
t_sum += elapsed_time;
t2_sum += elapsed_time * elapsed_time;
}
cudaEventDestroy(start);
cudaEventDestroy(stop);
}
const float t_ave = t_sum / NUM_REPEATS;
const float t_err = sqrt(t2_sum / NUM_REPEATS - t_ave * t_ave);
printf("Time = %g +- %g ms.\n", t_ave, t_err);
try
{
check(z,Number);
}
catch(int error)
{
printf("数据在%d位置处发生了错误",error);
return 0;
}
printf("no error");
free(x);
free(y);
free(z);
return 0;
} 依旧用nvcc来编译程序,需要注意编译选项,C++程序的性能显著依赖优化选项,总是采用-O3选项,且将DUSE_UP作为编译选项,程序中的USE_UP将有定义,从而使用单精度数,否则使用双精度数。我们用如下命令编译程序:
nvcc -O3 -arch=sm_75 -DUSE_DP add1cpu.cu
将得到一个单精度浮点型可执行文件,运行该函数,将得到add()函数运行的时间,大致为80ms。若用以下命令编译程序:
nvcc -O3 -arch=sm_75 -DUSE_DP add1cpu.cu
所用时间为160ms大致为单精度浮点型的两倍。
5.1.2 为CUDA程序计时
类似的在第四章cuda程序的基础上进行修改得到add2.gpu.cu,并进行计时:
#include
#include
#include
#include "error.cuh"
# ifdef USE_UP
typedef double real;
const real epsilon=1.0e-15
# else
typedef float real;
const real epsilon=1.0e-6;
# endif
const real a=1.23;
const real b=2.34;
const real c=3.57;
__global__ void add(const real *x,const real *y, real *z,const int N);
void __host__ check(const real *z,const int N);
const int numadd=0;
int main()
{
const int n=1e7+1;
const int m=n*sizeof(real)
real x=(real*)malloc(m);
real *h_y=(real*)malloc(m);
real *h_z=(real*)malloc(m);
for(int i=0;i>>(d_x,d_y,d_z,n);
cudaEventRecord(stop);
cudaEventSynchronize(stop);
float elapsedtime=0;
cudaEventElapsedTime(&elapsedtime,start,stop);
cudaEventDestroy(start);
cudaEventDestroy(stop);
if (i > 0)
{
t_sum += elapsedtime;
t2_sum += elapsedtime * elapsedtime;
}
printf("Time = %g ms.\n",elapsedtime);
}
const float t_ave = t_sum / numadd;
const float t_err = sqrt(t2_sum / numadd - t_ave * t_ave);
printf("Time = %g +- %g ms.\n", t_ave, t_err);
CHECK(cudaMemcpy(h_z,d_z,m,cudaMemcpyDeviceToHost));
check(h_z,n);
free(h_x);
free(h_y);
free(h_z);
CHECK(cudaFree(d_x));
CHECK(cudaFree(d_y));
CHECK(cudaFree(d_z));
return 0;
}
__global__ void add(const double *x,const double *y, double *z,const int N)
{
int tid=threadIdx.x+blockDim.x*blockIdx.x;
if(tidepsilon)
{
has_error=true;
break;
}
}
printf("%s\n",has_error?"Error":"no Error");
} 分别使用:
nvcc -O3 -arch=sm_75 add2gpu.cu
和 nvcc -O3 -arch=sm_75 -DUSE_DP add2gpu.cu进行编译,在装有GeForce MX450的机器中测试,单精度浮点核函数所用时间为2.42ms,而使用双精度浮点型的所用时间为4.84,双精度时间大致为单精度时间的两倍。
还可以计算数组数组想加问题在GPU中达到的有效现存带宽(effective memory bandwidth),其定义是GPU在单位时间内访问设备内存的字节。以本机GeForceMX450,显存带宽为80GB/s,其有效显存带宽为:
3e7*4B/2.4*10e-3s=50GB/s
可见有效显存带宽略小于理论显存带宽,进一步说明该问题是访存主导的,即浮点数中计算所占比例可忽略不计。
在上述程序中仅仅对于核函数进行了计时,尝试将数据复制的操作也放入被计时的代码段中,得到程序add3memcpy。可以发现我们是用GeForce MX450使用单、双精度时分别共耗时36ms、70ms,可以看到核函数的计算时间不到复制时间的5%,若将CPU与GPU中的数据传输时间也加上,CUDA程序相对于C++程序得到的不是性能提升,而是性能下降,总之若一个计算任务仅仅是将来自主机中的两个数组相加,并且要将结果传回host。那么什么样的任务能够用GPU获得加速呢。
在CUDA工具箱中有一个称为nvprof的可执行文件,可用于对于CUDA程序进行更多性能上的剖析,,用如下命令进行:
nvprof a.exe
若遇到了Uable to profile application.Unified Memory profilingfailed,可以将命令换为
nvprof --unified-memory-profiling off a.exe
得到的结果如下: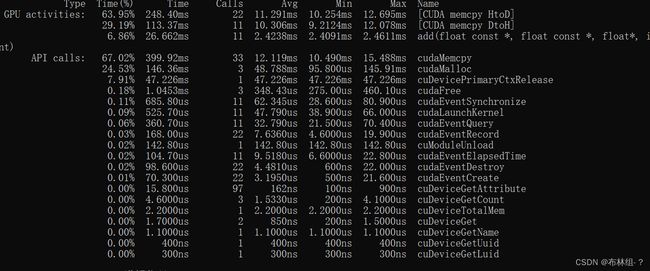
第一列是此处列出的每类操作所用时间的百分比,第二列是操作的总时间,第三列是每类操作所用的次数,第四列是每类操作的平均时间,第五列和第六列是每类操作所用时间的最小和最大调用时间,第七列是每类操作的名称。与cuda事件获得结果一致。
5.2 几个影响GPU加速的关键
5.2.1 数据传输的比例
从5.1节可以知道若一个程序仅仅为了计算两个数组的和,那么用GPU可能比用CPU还慢,因为花在数据传输(CPU和GPU之间)比计算时间要长的多。GPU计算核心和设备内存之间的数据传输的峰值理论带宽要远高于GPU和CPU之间的传输带宽,GeForce MX450的显存带宽理论值是80GB/s,而常用连接GPU和CPU内存的PCIe ×16 Gen3仅为16GB/s,相差数倍,要获得客观的GPU加速,就需要尽量缩减数据传输所花时间的比例。避免过多的数据进过PCIe传递。这是CUDA编程中较为重要的原则之一。
假设计算任务不是做一次数组相加的计算,而是做10000次数组相加的计算,而且只需要在开始和结束进行数据传输,那么数据传输所占的比例将可以忽略不计,此时CUDA程序的性能大大提高。
5.2.2 算术强度
在前面的测试中可以发现在装有GeForce MX450的计算机上,数组相加的核函数比对应的C++函数快20倍左右(这是没有对C++程序进行深度优化所得到的结果,本章不讨论深度优化问题),这是一个可观的加速比,但还没到极限。对于很多计算问题,能得到更高的加速比,是因为该问题算术强度不高。而一个问题的算术强度指的是其中算术操作的工作量与必要的内存操作的工作量之比,例如在数组相加的问题中,再对每个数据进行求和时需要先将数据取出来,然后再实施求和运算,最后将结果存放在设备内存中。这个问题的计算强度不高,因为在取两次数据、存一次数据的情况下只做了一次求和运算。在CUDA中设备内存的读写代价都很昂贵。
设备内存的访问速度取决于GPU的显存带宽。以GeForce MX450为例,其显存带宽的理论值为80GB/s.相比之下该GPU的单精度浮点数计算的峰值为1.51TFLOPS,意味着该GPU的理论寄存器带宽为:
4B×4(每个FMA的操作数)*1.51*e12/2(每个FMA的浮点数操作次数)=12TB/s
这里的FMA指fused multiply-add指令,即涉及4个操作数和两个浮点数的运算d=a*b+c.由此可见该GPU中的数据存取比浮点数计算慢100倍左右,对其他GPU也可以做类似分析,如果一个计算中不仅是简单地求和操作,而是更为复杂的浮点数运算,那么就有可能得到更高的加速比。为了得到更高的算术强度,将之前的程序数组相加函数进行修改,给出了修改后的主机函数和核函数:
const real x0=100.0;
void arithmetic(real *x,const real x0,const int N)
{
for(int n=0;n也就是说在核函数中不再是一次相加计算,而是一个10000次的循环,而且在循环过程中使用了数学函数sqrt(),程序可通过以下选项进行计算, arthmetic1cpu.cu,若需采用双精度浮点型计算,则添加 -DUSE_DP
nvcc -O3 -arch=sm_75 arthmetic1cpu.cu 后运行a.exe
arthmetic1gpu.cu可以用以下方式编译和运行:
nvcc -O3 -arch=sm_75 arithmetic2gpu.cu
并在调用时传一个参数
a.exe N
#include "error.cuh"
#include
#include
#ifdef USE_DP
typedef double real;
#else
typedef float real;
#endif
const int NUM_REPEATS = 10;
const real x0 = 100.0;
void __global__ arithmetic(real *x, const real x0, const int N);
int main(int argc, char **argv)
{
if (argc != 2)
{
printf("usage: %s N\n", argv[0]);
exit(1);
}
const int N = atoi(argv[1]);
const int block_size = 128;
const int grid_size = (N + block_size - 1) / block_size;
const int M = sizeof(real) * N;
real *h_x = (real*) malloc(M);
real *d_x;
CHECK(cudaMalloc((void **)&d_x, M));
float t_sum = 0;
float t2_sum = 0;
for (int repeat = 0; repeat <= NUM_REPEATS; ++repeat)
{
for (int n = 0; n < N; ++n)
{
h_x[n] = 0.0;
}
CHECK(cudaMemcpy(d_x, h_x, M, cudaMemcpyHostToDevice));
cudaEvent_t start, stop;
CHECK(cudaEventCreate(&start));
CHECK(cudaEventCreate(&stop));
CHECK(cudaEventRecord(start));
cudaEventQuery(start);
arithmetic<<>>(d_x, x0, N);
CHECK(cudaEventRecord(stop));
CHECK(cudaEventSynchronize(stop));
float elapsed_time;
CHECK(cudaEventElapsedTime(&elapsed_time, start, stop));
printf("Time = %g ms.\n", elapsed_time);
if (repeat > 0)
{
t_sum += elapsed_time;
t2_sum += elapsed_time * elapsed_time;
}
CHECK(cudaEventDestroy(start));
CHECK(cudaEventDestroy(stop));
}
const float t_ave = t_sum / NUM_REPEATS;
const float t_err = sqrt(t2_sum / NUM_REPEATS - t_ave * t_ave);
printf("Time = %g +- %g ms.\n", t_ave, t_err);
free(h_x);
CHECK(cudaFree(d_x));
return 0;
}
void __global__ arithmetic(real *d_x, const real x0, const int N)
{
const int n = blockDim.x * blockIdx.x + threadIdx.x;
if (n < N)
{
real x_tmp = d_x[n];
while (sqrt(x_tmp) < x0)
{
++x_tmp;
}
d_x[n] = x_tmp;
}
}
注意:这里的CUDA版本的可执行文件在运行时需要提供一个命令行参数N。
该参数将赋值给程序中的变量N,相关代码如下:
if(argc!=2)
{
printf("usage :%s N\n",argv[0]);
}
constn int N=atoi(argv[1]);
继续在装有GeForce NX450的计算机中进行测试:当数组程度为10000时,主机执行时间为100ms(单精度)和148ms(双精度);当数组长度为1e6时,执行时间为61ms(单精度)和2312ms(双精度),因为核函数和主机函数处理的数组长度相差100倍,所以在使用单精度和双精度浮点数时,GPU和CPU的加速比分别为:
100ms×100/61ms=150
和
140ms×100/2312ms=9
可见提高算术强度能够显著提升GPU相对于CPU的加速比。当算术强度很高的时候,GeForce系列的GPU的单精度浮点数的计算能力就能充分的发挥出来,在我们的版本中,单精度版本的核函数是双精度版本的36倍之多,接近理论值32,进一步说明该问题是计算主导,而不是访存主导。
5.2.3 并行规模
另一个影响CUDA程序性能的因素是并行规模。并行规模可用GPU中的线程数目来衡量。从硬件的角度出发,一个GPU由多个流多处理器(streaming multiprocessor,SM)构成,而每个SM中有多个CUDA核心。每个SM是相对独立的。从开普勒架构到伏特架构,一个SM中最多能驻留的线程是2048,,对于图灵架构,该数目是1024,一块GPU中一共可以驻存几万到几十万个线程,如果核函数中定义了线程数目远小于这个数,将很难得到高的加速比。
5.2.4 总结
通过本节的力磁,可以看到,一个CUDA能获取到高性能条件有以下即几点:
(1)数据传输比例较小。
(2)核函数的算术强度较高。
(3)核函数中定义的线程数较多.
所以在编写与优化CUDA程序时,一定要想方设法的(主要指仔细设计算法)并做到以下几点:
(1)减小主机与设备之间的数据传输。
(2)提高核函数的计算强度。
(3)增大核函数的并行规模。
5.3 CUDA中的数学函数库
前面使用了求平方根的数学函数。在CUDA数学库中,还有许多类似函数,如幂函数、指数函数、对数函数等,这些函数可以在以下网站进行查询:http://docs.nvidia.com/cuda/cuda-math-api
可以归纳如下:
(1)单、双、半精度浮点数、整数、类型转换内建函数和数学函数(single、double presion instrinsics and math functions)。使用单、双函数时不需要包含任何额外的头文件,半精度需要使用
(2)“单指令-多数据”内建函数,不需要包含头文件。
例如:
double sqrt(double x);
float sqrt(float x);
float sqrtf(float x);
内建函数指的是一些住阿奴额率较低,但效率较高的函数,例如以下求平方根的内建函数:
float __fsqrt_rd(float x);//round-down mode
float __fsqrt_rn(float x);//round-to_nearnest_even mode等