Java实现：利用前序遍历和中序遍历构造二叉树，并从上往下打印每个节点

题目：

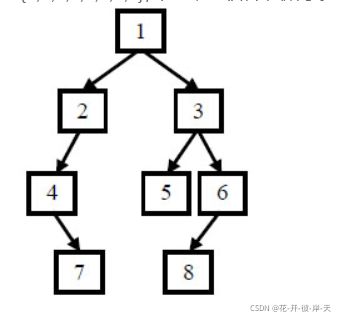
	给定 二叉树的前序遍历和中序遍历结果，请重建出该二叉树并按照从上往下的顺序打印每个节点。

前序遍历：[1,2,4,7,3,5,6,8]
中序遍历：[4,7,2,1,5,3,8,6]
打印输出：1，2，3，4，5，6，7，8

注：
代码写的很潦草，打印出的二叉树很简单，观赏性不强

代码

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int var) {
        this.val = var;
    }
}

public class Test {
    public static void main(String[] args) {
        int []pre={1,2,4,7,3,5,6,8};
        int in[]={4,7,2,1,5,3,8,6};
        //得到构建的二叉树的根节点
        TreeNode data=getRealTree(pre,in);
        ArrayList<Integer> treeList=getTree(data);
        for(Integer a:treeList){
            System.out.print(a+" ");
        }
    }
    //根据前序和中序构建二叉树，并返回其根节点
    public static TreeNode getRealTree(int pre[],int in[]){
        //结束方法的条件
        if(pre==null||pre.length==0){
            return null;
        }

        //确定根节点，注意：前序遍历的第一个节点就是树的根节点
       TreeNode root=new TreeNode(pre[0]);
        //找到根节点在中序遍历中的位置
        int index=findIndex(pre,in);
        /**
         * 构建左子树：左子树=（左子树的前序数组，左子树的中序数组）
         * 构建右子树：右子树=（右子树的前序数组，右子树的中序数组）
         *
         * 中序遍历：
         *          因为前序遍历的第一个节点就是树的根节点；
         *          找到根节点在中序遍历中的位置，其前面的就是左子树的中序遍历，后面的就是右子树的中序遍历
         * 前序遍历：
         *          根据中序遍历，可以找到根节点的左右子树的个数
         */
        root.left=getRealTree(Arrays.copyOfRange(pre,1,index+1),Arrays.copyOfRange(in,0,index));
        root.right=getRealTree(Arrays.copyOfRange(pre,index+1,pre.length),Arrays.copyOfRange(in,index+1,in.length));
        return root;
    }
    //返回中序遍历中与pre[0]相等的节点的索引
    public static int findIndex(int []pre,int []in){
        for(int i=0;i<in.length;i++){
            if(pre[0]==in[i]){
                return i;
            }
        }
        return 0;
    }
    /**
     * 从上往下打印二叉树：
     *               每一次打印一个节点的时候，若是有子节点，则将其子节点放在队列的末尾；接下来队列的头部拿出最早入队的节点，重复之前的过程，直到所有节点被打印
     */
    public static ArrayList<Integer> getTree(TreeNode head){
        if(head==null){
            return null;
        }
        ArrayList<Integer> list=new ArrayList<>();
        Queue<TreeNode> queue=new LinkedList<>();

        //传入的根节点放入队列，以进行下面的循环
        queue.offer(head);

        while (!queue.isEmpty()){
            //队列不为空，则队首是本次遍历的头节点，遍历后，本次队首会被移除
            TreeNode root=queue.poll();
            //本次打印是从上往下，从左往右依次进行，所以左节点先入队
            if(root.left!=null){
                queue.offer(root.left);
            }
            //节点入队
            if(root.right!=null){
                queue.offer(root.right);
            }
            //把本次循环中的队首放入list集合
            list.add(root.val);
        }
        return list;
    }
}