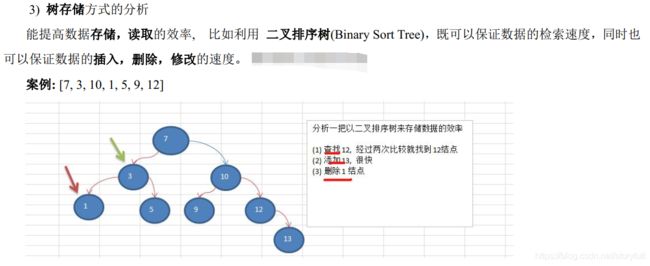
数据结构与算法 树与树算法(主讲二叉树)最全的二叉树讲解,让你弄懂所有的二叉树!二叉树的遍历 二叉树的非递归遍历 二叉树的深度遍历
阅读目录
-
-
- 树的相关概念
-
- 为什么需要树结构
- 树的概念
- 树的术语
- 树的种类
- 常见的一些树的应用场景
- 树的存储与表示
-
- 顺序存储
- 链式存储
- 二叉树基础
-
- 二叉树的基本概念
- 二叉树的五种形态
- 二叉树的性质(特性)
- 二叉树的分类
-
- 完全二叉树(Complete Binary Tree)
- 满二叉树
-
- 国内定义
- 国外定义
- 完满二叉树(Full Binary Tree)
- 二叉树种类的对比
-
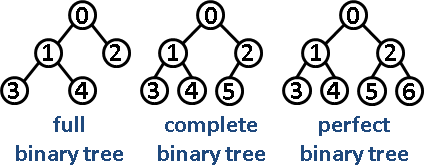
- 完美(Perfect)二叉树 vs. 完全(Complete)二叉树
- 完全(Complete)二叉树 vs. 完满(Full)二叉树
- 完满(Full)二叉树 vs. 完全(Complete)二叉树 vs. 完美(Perfect)二叉树
- 二叉树的实现(Python)
-
- 二叉树的结点表示
- 树的创建
- 二叉树的遍历
-
- 广度遍历
-
- 广度遍历的实现
- 添加结点的过程剖析
- 深度遍历
- 深度遍历的三种实现模式
-
- 先序遍历
- 中序遍历
- 后序遍历
- 非递归实现树的三种深度遍历
- Python完整实现二叉树的功能
-
树的相关概念
为什么需要树结构
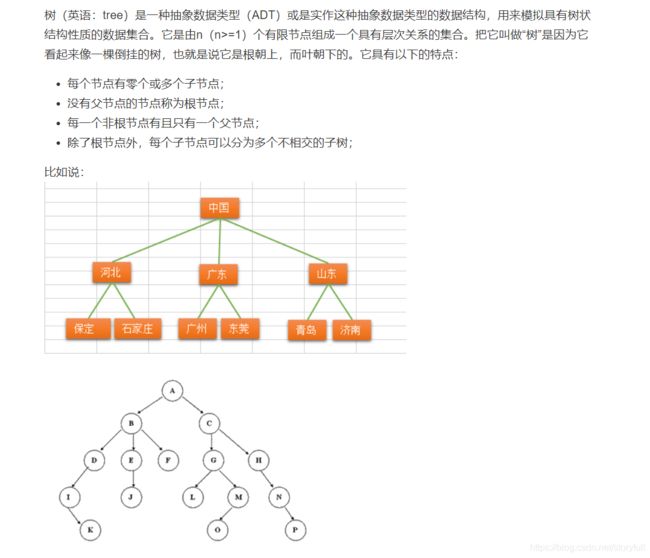
树的概念
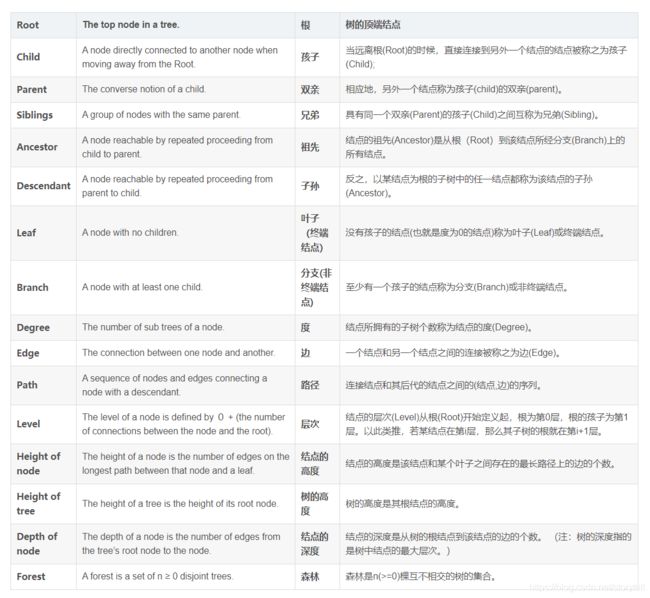
树的术语
-
结点的权:就是每个结点的值
-
结点的度:一个节点含有的子树的个数称为该结点的度;↓↓↓(图1-1-1)
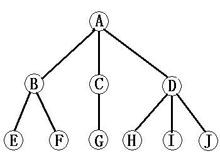
如图:A结点的度为3,B结点的度为2,c结点的度为1,D结点的度为3
E、F、G、H、I 以及J度都为0 -
树的度:一棵树中,最大的结点的度称为树的度;(图1-1-1)中树的度为 3
-
叶结点(终端结点):度为 0 的结点;一棵树当中没有子结点(即度为0)的结点称为叶子结点,简称“叶子”。 叶子是指出度为0的结点,又称为终端结点
-
父亲结点(父结点):若一个结点含有子结点,则这个结点称为其子结点的父结点;
-
孩子结点(子结点):一个结点 含有子树的根结点 称为 该结点的 子结点;
-
兄弟结点:具有 相同父结点的结点 互称为 兄弟结点;
-
结点的层次:从根 开始定义起,根为 第1层,根的子结点 为第2层,以此类推;
-
树的高度或深度:树中 节点的 最大层次;
-
堂兄弟结点:父结点 在同一层的结点 互为堂兄弟;
-
结点的祖先:从 根 到 该结点 所经 分支上的 所有结点;
-
子孙:以 某结点为根的子树中 任一结点 都称为该结点的子孙。
-
森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的种类
-
无序树:树中任意结点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树;
-
有序树:树中任意结点的子结点之间有顺序关系,这种树称为有序树;
-
二叉树:每个结点最多含有两个子树的树称为二叉树;
下面的种类 不在本篇文章叙述,每个都会开一篇文章来整理性质、算法实现、以及应用
-
平衡二叉树(AVL树):当且仅当任何结点的两棵子树的高度差不大于1的二叉树;
-
排序二叉树(二叉查找树(英语:Binary Search Tree),也称二叉搜索树、有序二叉树);
-
霍夫曼树(用于信息编码):带权路径最短的二叉树称为哈夫曼树或最优二叉树;
-
B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树。
-
红黑树(平衡二叉查找树)
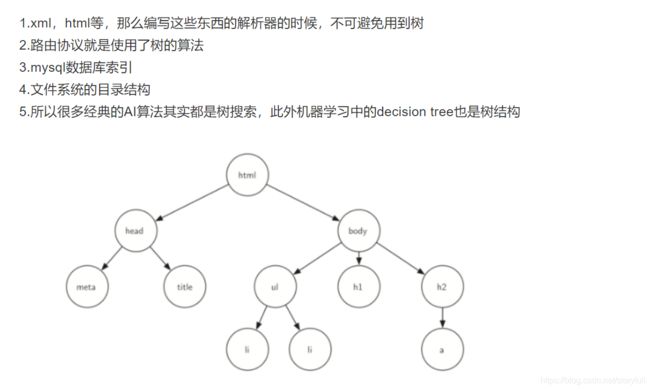
常见的一些树的应用场景
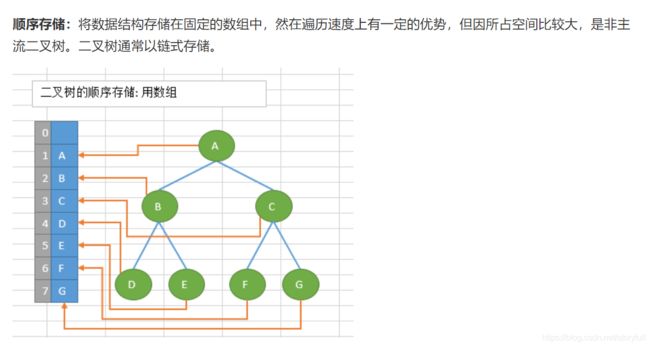
树的存储与表示
顺序存储
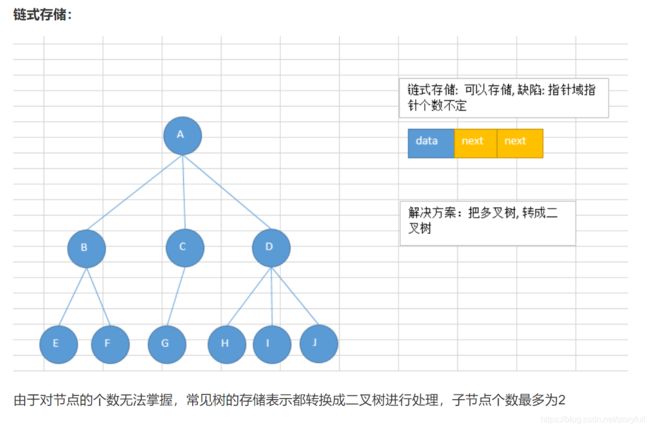
链式存储
二叉树基础
二叉树的基本概念
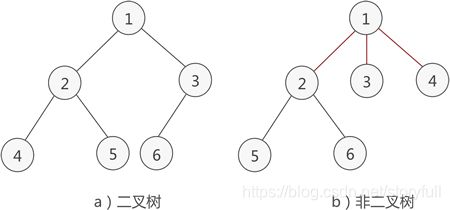
二叉树是每个节点最多有两个子树的树结构。
通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)二叉树是每个节点最多有两个子树的树结构。
满足以下两个条件的树就是二叉树:
1.本身是有序树;
2.树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树的五种形态
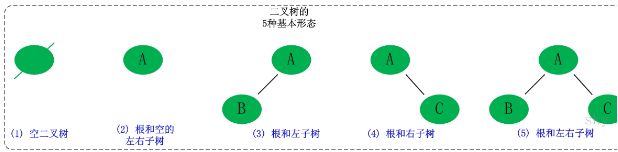
二叉树是每个节点最多有两个子树的树结构。
它有五种基本形态:
二叉树可以是空集;左、右子树皆为空根;可以有空的左子树或右子树;根和左右子树
二叉树的性质(特性)
-
在二叉树的第 i 层上至多有 2^(i-1) 个结点(i>0)
例如:只有1层,即只有一个根节点,即是第i=1层只有2^0 个节点;
当有两层时,第i=2层,有2^1个节点 -
深度为 k 的二叉树 至多 有 2^k - 1个结点(k>0)
-
对于任意一棵二叉树,如果其叶结点数为 N0,而度数为2的结点总数为N2,则N0=N2+1;
具有n个结点的完全二叉树的深度必为 log2(n+1) -
对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外)
二叉树的分类
完全二叉树(Complete Binary Tree)
'''
A Complete Binary Tree (CBT) is a binary tree in which every level,
except possibly the last, is completely filled, and all nodes
are as far left as possible.
'''
若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树
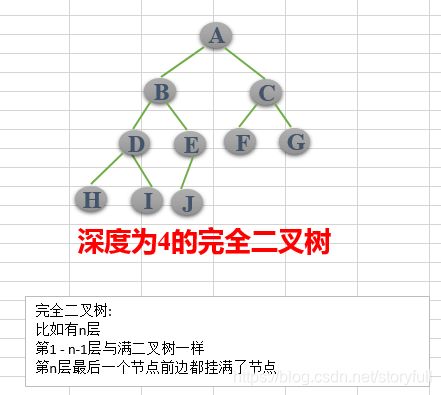
叶子结点只可能在(深度)最大的两层上出现!
对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或 L+1;
出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:
var tree:array[1…n]of longint;{n:integer;n>=1}
对于tree[i],有如下特点:
(1)若i为奇数且i>1,那么tree的左兄弟为tree[i-1];
(2)若i为偶数且i
(4)若2i<=n,那么tree的左孩子为tree[2i];若2i+1<=n,那么tree的右孩子为tree[2i+1];
(5)若i>n div 2,那么tree[i]为叶子结点(对应于(3));
(6)若i<(n-1) div 2.那么tree[i]必有两个孩子(对应于(4))。
(7)满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
完全二叉树第 i 层至多有 2 ^ (i-1) 个节点,共 i 层的完全二叉树总共最多有 2^i - 1个节点。
完全二叉树的特点是:
1)只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现;
2)对任一结点,如果其右子树的深度为 j,则其左子树的深度必为 j 或 j+1。 即度为1的点只有1个或0个
满二叉树
国内定义
-
从图形形态上看,满二叉树外观上是一个三角形。
-
从数学上看,满二叉树的各个层的结点数形成一个首项为1,公比为2的等比数列。
因此由等比数列的公式,满二叉树满足如下性质。
1、一个层数为 k 的满二叉树总结点数为:2^k - 1,因此满二叉树的结点数一定是奇数个。
2、第 i 层上的结点数为: 2^(i-1)
3、一个层数为 k 的满二叉树的叶子结点个数(也就是最后一层):2^(k-1)
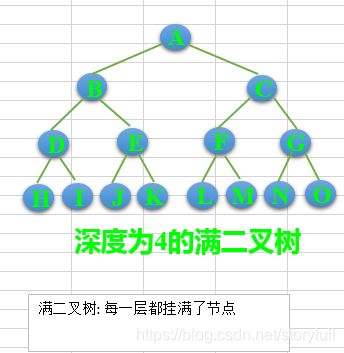
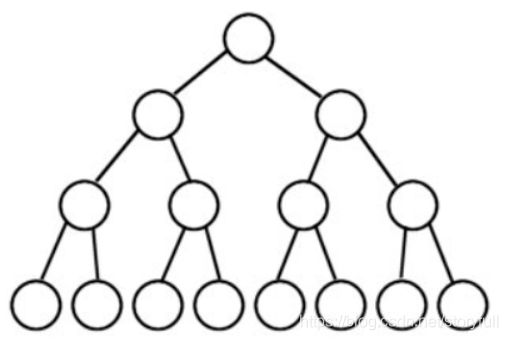
国内的定义,即是指的“完美二叉树” -
完美二叉树(Perfect Binary Tree)
A Perfect Binary Tree(PBT) is a tree with all leaf nodes at the same depth.
All internal nodes have degree 2
国外定义
满二叉树的结点,要么是 叶子结点的度 为0,要么是 度为 2 的结点,不存在度为1的结点。
这就是“完满二叉树/严格二叉树”
因此,下图中这个二叉树也是满二叉树。但是按照国内的定义,它却不是满二叉树
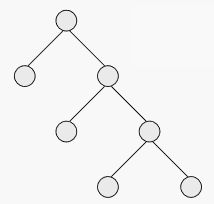
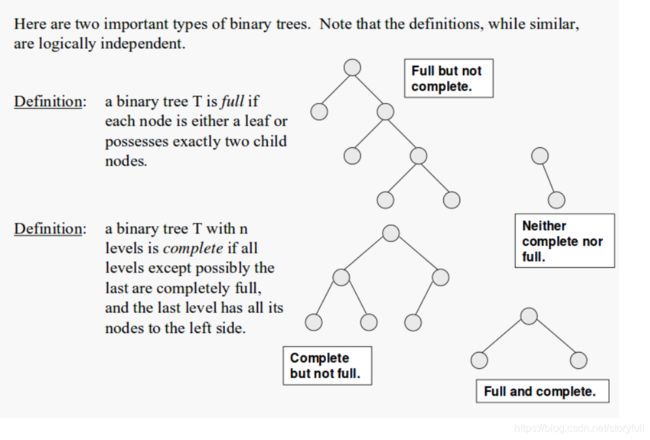
完满二叉树(Full Binary Tree)
A Full Binary Tree (FBT) is a tree in which every node other than the leaves has two children.
注:Full Binary Tree又叫做Strictly Binary Tree (严格二叉树)
所有非叶子结点的度都是2。(只要你有孩子,你就必然是有两个孩子。)
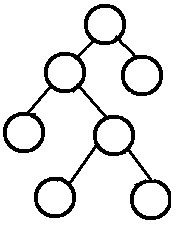
二叉树种类的对比
完美(Perfect)二叉树 vs. 完全(Complete)二叉树
完美(Perfect)二叉树,国内指:满二叉树
下面是一棵完美二叉树(满二叉树) ↓↓↓ (图:3-5-1)

如果将编号为15, 14, …, 9的叶子结点从右到左依次拿掉或者拿掉部分,则是一棵完全(Complete)二叉树,例如,将上图中的编号为15, 14, 13, 12, 11叶子结点都拿掉(从右到左的顺序),下图就是一棵完全二叉树 ↓↓↓(图:3-5-2)

下图不是一棵完全二叉树,因为最底层不是完整时,没有全部靠左侧,需要将 11(K)移动到 5(E)的右下方,才是一棵完全二叉树! ↓↓↓(图:3-5-3)
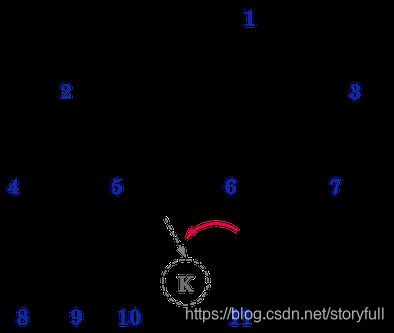
完全(Complete)二叉树 可以借助于栈(stack)的思想来理解。
例如把图3-5-1中的完美(Perfect)二叉树的所有结点按照编号1, 2, 3, …, 15依次入栈(push)。
那么,对栈的每一次出栈(pop)操作后,都是按照:“ 右 - 左 - 根 ” ,即是 “后进先出 ”!
栈 对于 完美 和 完全 和 完满 二叉树 都适用
完全(Complete)二叉树 vs. 完满(Full)二叉树
完全二叉树:最底层,结点从右往左,可以出现单独一个结点,但是只能在左边
完满二叉树:最底层,结点从右往左,只能出现两个的结点,或者0个,不能单独出现
完满(Full)二叉树 vs. 完全(Complete)二叉树 vs. 完美(Perfect)二叉树
-
完美(Perfect)二叉树一定是完全(Complete)二叉树,但完全(Complete)二叉树不一定是完美(Perfect)二叉树。
-
完美(Perfect)二叉树一定是完满(Full)二叉树,但完满(Full)二叉树不一定是完美(Perfect)二叉树。
-
完全(Complete)二叉树可能是完满(Full)二叉树,完满(Full)二叉树也可能是完全(Complete)二叉树。
-
既是完全(Complete)二叉树又是完满(Full)二叉树也不一定就是完美(Perfect)二叉树。
二叉树的实现(Python)
二叉树的结点表示
class Node(object): # 创建结点
def __init__(self, data=-1, left_child=None, right_child=None):
self.data = data
self.left_child = left_child
self.right_child = right_child
'''
一个二叉树结点可以包括有两个分支,左右;也可以为空;
都用默认值参数更为贴切(左右可以直接都为空):
即你如果实例结点时,
不通过参数传入值,我就默认为空
其中data 时必须要通过参数传入的,给它一个默认值,如果没传入,值为-1 错误信息
'''
树的创建
class Tree(object): # 创建一个树的类,并给一个root根节点,一开始为空,随后添加节点
def __init__(self, root=None):
self.root = root
def add(self, data): # 树的添加 操作
node = Node(data) # 实例一个结点
if self.root is None: # 如果树为空,即没有根结点
self.root = node # 给树构建一个根结点
return # 注意这个return
queue = [self.root] # 这一步表示,已经有了根结点,将它取出放到队列里
while queue: # 接下来遍历队列
cur = queue.pop(0) # 弹出队列的第一个元素(结点),pop默认pop(-1)
if cur.left_child is None: # 如果 结点左侧没有子结点
cur.left_child = node
return
else: # 如果 左侧存在子结点
queue.append(cur.left_child) # 将左侧的子结点 添加到 队列中
if cur.right_child is None: # 如果 结点右侧没有子结点
cur.right_child = node
return
else: # 如果 右侧侧存在子结点
queue.append(cur.right_child) # 将右侧的子结点 添加到 队列中
二叉树的遍历
树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问,即依次对树中每个结点访问一次且仅访问一次,我们把这种对所有节点的访问称为遍历(traversal)。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归,广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现!
广度遍历
广度遍历的实现
class Node(object): # 创建结点类
def __init__(self, data, left_child=None, right_child=None):
self.data = data
self.left_child = left_child
self.right_child = right_child
class Tree(object): # 创建一个树的类,并给一个root根节点,一开始为空,随后添加节点
def __init__(self, root=None):
self.root = root
def add(self, data): # 树的添加 操作
node = Node(data) # 实例一个结点
if self.root is None: # 如果树为空,即没有根结点
self.root = node # 给树构建一个根结点
return
queue = [self.root] # 到这表示(至少进行到添加第二个元素),已有根结点,将它取出放到队列
while queue: # 接下来遍历队列
cur = queue.pop(0) # 弹出队列的第一个元素(结点),pop默认pop(-1)
if cur.left_child is None: # 如果 结点左侧没有子结点
cur.left_child = node
return
else: # 如果 左侧存在子结点
queue.append(cur.left_child) # 将左侧的子结点 添加到 队列中
if cur.right_child is None: # 如果 结点右侧没有子结点
cur.right_child = node
return
else: # 如果 右侧侧存在子结点
queue.append(cur.right_child) # 将右侧的子结点 添加到 队列中
def breadth_travel(self): # 广度遍历
if self.root is None:
return
queue = [self.root]
while queue:
cur = queue.pop(0)
print(cur.data, end=" ")
if cur.left_child is not None:
queue.append(cur.left_child)
if cur.right_child is not None:
queue.append(cur.right_child)
if __name__ == '__main__':
t = Tree()
for i in range(10):
t.add(i)
t.breadth_travel()
广度遍历输出结果:0 1 2 3 4 5 6 7 8 9
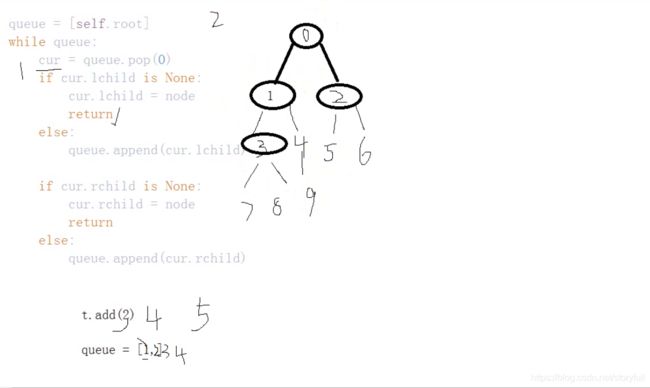
添加结点的过程剖析
-
首先实例化并且给二叉树添加0-9间的10个树结点,所以 t.add(i) 会被调用10次;注意每次add函数都要从头走到尾;queue 每次都会先存放一个根结点(按照数字应该是data为0的结点),取得时候总是先取到它。
-
queue.pop(0) 将根结点抛出,通过判断能得到根结点(i=0,data=0)(注意作为通过Node实例得到的结点给了self.root后,里面必然封装到了 left_child 和 right_child 两个实例变量(字段),所以 cur 接收到后,才能使用它们)完成根结点,退出循环后;接着判断根结点(i=0,data=0)的cur.left_child是否为空,上例为空,则将结点(i=1,data=1)挂上,此时遇到return直接退出函数;接着(i=2,data=2),此时依然是在根结点上判断,因为queue现在只会存放一个根结点,pop出来的也只有根结点而已,接着此时根结点左侧已经不为空了,走else,将左侧的孩子添加到队列queue中去,此时队列中存放的元素为[1, ] (注意开头是在pop(0)的基础上,所以根结点已经不在了),所以只会存放左侧子结点),因为还没遇到return 所以还会接着运行,判断右侧有没有孩子啊,结果没有,所有将 (i=2,data=2)挂到右侧,此时遇到return退出函数
-
退出函数后,此时根结点(data=0,i=0)左右两侧已经挂满了结点;接着 (i=3,data=3),又要从根结点开始判断,不过因为左右两侧都挂了结点,两次都会先直接走else分支,所以只会给 队列queue里重新添加值[1,2] (队列是先进先出,2应该在后面),到 (i=3,data=3)这次了,pop出来的应该是(data=1)这个结点了,判断它左侧没有孩子,所以 (i=3,data=3) 这个结点就挂在它的左侧,遇到return退出!
-
当 (i=4,data=4),依次重复上面的步骤,此时队列queue抛出的(data=1)这个结点,它的左侧已经有值了,先在queue里存放下 (i=3,data=3) ,所以为[2,3] (1已经抛出),接着判断它右侧没有孩子,则挂上
-
当 (i=5,data=5),也是重复上述步骤,挂到4时,(data=1)结点左右两侧已经满了,所有按步骤走,队列queue会抛出2 ,依次判断2左右两侧,然后依次挂上结点…
-
从上面的不走可以看出,每次新增子结点都要重头判断一遍,时间复杂度还是很高的
深度遍历
对于一颗二叉树,深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点,尽可能深的搜索树的分支。
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点,它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历(preorder),中序遍历(inorder)和后序遍历(postorder)。我们来给出它们的详细定义,然后举例看看它们的应用。
深度遍历的三种实现模式
先序遍历
先序遍历 在先序遍历中,我们先访问根节点,然后递归使用先序遍历访问左子树,再递归使用先序遍历访问右子树
根节点->左子树->右子树
def preorder(self, node):
"""递归实现先序遍历"""
if node is None:
return
print(node.data, end=" ")
self.preorder(node.left_child)
self.preorder(node.right_child)
中序遍历
中序遍历 在中序遍历中,我们递归使用中序遍历访问左子树,然后访问根节点,最后再递归使用中序遍历访问右子树
左子树->根节点->右子树
def inorder(self,node):
if node is None:
return
self.inorder(node.left_child)
print(node.data, end=" ")
self.inorder(node.right_child)
后序遍历
后序遍历 在后序遍历中,我们先递归使用后序遍历访问左子树和右子树,最后访问根节点
左子树->右子树->根节点
def postorder(self,node):
if node is None:
return
self.preorder(node.left_child)
self.preorder(node.right_child)
print(node.data, end=" ")
非递归实现树的三种深度遍历
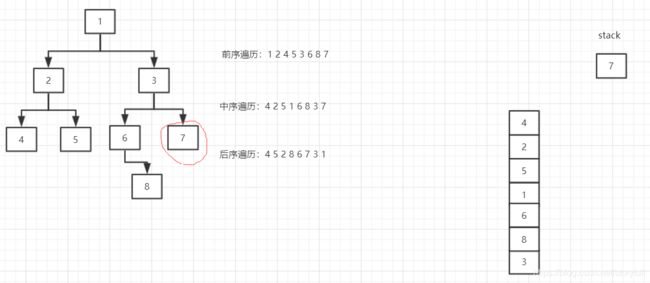
只为演示非递归实现深度遍历(下图中并非严格意义上的二叉树,但不影响,只为看顺序)
图解:非递归,栈的方式实现三种深度遍历
- 第一步:将存在的左树结点都先压入栈内,栈顶元素为最后一个左树结点
- 第二步:pop出栈顶元素,将当前的右树结点当作根结点,然后循环添加当前根结点的右树结点,直到没有后退出循环;再去pop栈顶元素上后一个元素,将它作为根结点,取添加它的右树结点,重复操作,直到栈内没有元素(开始压入的左树结点,栈底是“1结点”),此时就来处理右侧了;详细过程看下面的图解↓↓↓
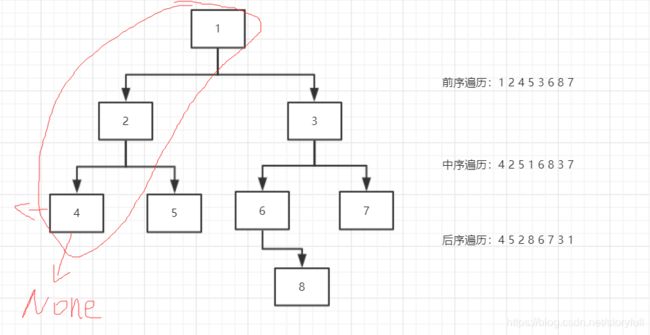


- 上面图解,最终会发现其实输出的就是中序遍历的结果,调整输出位置就能完成前序和中序深度遍历方式
- 【难点】但是 后序遍历方式 虽然循环的过程不变,但是 pop弹出的顺序要变,我们不能在没有pop完所有右树结点时,把根结点先pop出来,所有当压入完左树结点时,不能先pop,而是用赋值代替,即是:node = stack[-1],且 直到 先pop完所有右树结点:如下图解 ↓↓↓

- 下图右边已经遍历结束了,接下来要依次遍历左边,依然不能先pop “1结点”,只是通过stack[-1]赋值拿到



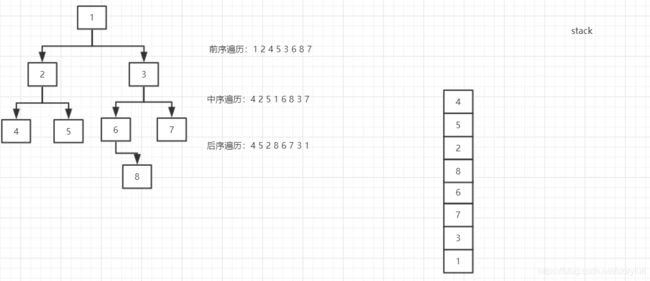
- 关于输出,pop谁打印谁即可
用栈来实现深度遍历,不用面向对象
class Node(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def pre_order(root): # 先序遍历
if root is None:
return None
stack = []
tmp_node = root
while tmp_node or stack:
while tmp_node:
print(tmp_node.val, end=" ")
stack.append(tmp_node)
tmp_node = tmp_node.left
node = stack.pop()
tmp_node = node.right
def in_order(root): # 中序遍历
if root is None:
return None
stack = []
tmp_node = root
while tmp_node or stack:
while tmp_node:
stack.append(tmp_node)
tmp_node = tmp_node.left
node = stack.pop()
print(node.val, end=" ")
tmp_node = node.right
def post_order(root): # 后序遍历(难点)
if root is None:
return None
stack = []
tmp_node = root
while tmp_node or stack:
while tmp_node:
stack.append(tmp_node)
tmp_node = tmp_node.left
node = stack[-1]
tmp_node = node.right
if node.right is None: # if tmp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
t1 = Node(1)
t2 = Node(2)
t3 = Node(3)
t4 = Node(4)
t5 = Node(5)
t6 = Node(6)
t7 = Node(7)
t8 = Node(8)
t1.left = t2
t1.right = t3
t2.left = t4
t2.right = t5
t3.left = t6
t3.right = t7
t6.right = t8
pre_order(t1)
print()
in_order(t1)
print()
post_order(t1)
改成 面向对象的写法 手动创建树的结点
class Node(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Tree(object):
def __init__(self, root=None):
self.root = root
def pre_order(self, root):
if root is None:
return None
stack = []
temp_node = root
while temp_node or stack:
while temp_node:
print(temp_node.val, end=" ")
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
temp_node = node.right
def in_order(self, root):
if root is None:
return None
stack = []
temp_node = root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
print(node.val, end=" ")
temp_node = node.right
def post_order(self, root):
if root is None:
return None
stack = []
temp_node = root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack[-1]
temp_node = node.right
if temp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
t1 = Node(1) # 这里没在Tree中新增添加结点的方法,所以只能手动创建结点了
t2 = Node(2)
t3 = Node(3)
t4 = Node(4)
t5 = Node(5)
t6 = Node(6)
t7 = Node(7)
t8 = Node(8)
t1.left = t2
t1.right = t3
t2.left = t4
t2.right = t5
t3.left = t6
t3.right = t7
t6.right = t8
obj = Tree()
obj.pre_order(t1)
print()
obj.in_order(t1)
print()
obj.post_order(t1)
面向对象 用方法来创建树的结点
class Node(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Tree(object):
def __init__(self, root=None):
self.root = root
def add(self, val): # 创建 树的结点
node = Node(val)
if self.root is None:
self.root = node
return
queue = [self.root] # 用队列来实现
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def pre_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
print(temp_node.val, end=" ")
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
temp_node = node.right
def in_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
print(node.val, end=" ")
temp_node = node.right
def post_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack[-1]
temp_node = node.right
if temp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
obj = Tree()
for i in range(1,9):
obj.add(i)
obj.pre_order()
print()
obj.in_order()
print()
obj.post_order()
注意,上面面向对象实现时,遍历方法没有传参数,因为class Tree 已经把根结点封装好了,
直接用就可以了,不需要传参;如果非要传也可以,只是最后实例时,需要传入参数,
这时只需要传入:对象.root 就行了 下面来实例一把
记住:如果用 递归实现遍历,就一定要传参数;非递归可以不用传参数
class TreeNode(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Tree(object):
def __init__(self):
self.root = None
def add_node(self, val):
node = TreeNode(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def bre_order(self):
if self.root is None:
return None
queue = [self.root]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, end=" ")
if temp_node.left:
queue.append(temp_node.left)
if temp_node.right:
queue.append(temp_node.right)
# def pre_order(self):
# if self.root is None:
# return None
# stack = []
# temp_node = self.root
# while temp_node or stack:
# while temp_node:
# print(temp_node.val, end=" ")
# stack.append(temp_node)
# temp_node = temp_node.left
# node = stack.pop()
# temp_node = node.right
#
# def in_order(self):
# if self.root is None:
# return None
# stack = []
# temp_node = self.root
# while temp_node or stack:
# while temp_node:
# stack.append(temp_node)
# temp_node = temp_node.left
# node = stack.pop()
# print(node.val, end=" ")
# temp_node = node.right
def pre_order(self, root):
if root is None:
return None
print(root.val, end=" ")
self.pre_order(root.left)
self.pre_order(root.right)
def in_order(self, root):
if root is None:
return None
self.in_order(root.left)
print(root.val, end=" ")
self.in_order(root.right)
def post_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack[-1]
temp_node = node.right
if temp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
obj = Tree()
for i in range(1, 9):
obj.add_node(i)
obj.bre_order()
print()
obj.pre_order(obj.root)
print()
obj.in_order(obj.root)
print()
obj.post_order()
Python完整实现二叉树的功能
递归完成遍历
class Node(object): # 创建结点类
def __init__(self, data, left_child=None, right_child=None):
self.data = data
self.left_child = left_child
self.right_child = right_child
class Tree(object): # 创建一个树的类,并给一个root根节点,一开始为空,随后添加节点
def __init__(self, root=None):
self.root = root
def add(self, data): # 树的添加 操作
node = Node(data) # 实例一个结点
if self.root is None: # 如果树为空,即没有根结点
self.root = node # 给树构建一个根结点
return
queue = [self.root] # 这一步表示,已经有了根结点,将它取出放到队列里
while queue: # 接下来遍历队列
cur = queue.pop(0) # 弹出队列的第一个元素(结点),pop默认pop(-1)
if cur.left_child is None: # 如果 结点左侧没有子结点
cur.left_child = node
return
else: # 如果 左侧存在子结点
queue.append(cur.left_child) # 将左侧的子结点 添加到 队列中
if cur.right_child is None: # 如果 结点右侧没有子结点
cur.right_child = node
return
else: # 如果 右侧侧存在子结点
queue.append(cur.right_child) # 将右侧的子结点 添加到 队列中
def breadth_travel(self): # 广度遍历
if self.root is None:
return
queue = [self.root]
while queue:
cur = queue.pop(0)
print(cur.data, end=" ")
if cur.left_child is not None:
queue.append(cur.left_child)
if cur.right_child is not None:
queue.append(cur.right_child)
# 递归实现三种深度遍历
def pre_order(self, node):
if node is None:
return
print(node.data, end=" ")
self.pre_order(node.left_child)
self.pre_order(node.right_child)
def in_order(self, node):
if node is None:
return
self.in_order(node.left_child)
print(node.data, end=" ")
self.in_order(node.right_child)
def post_order(self, node):
if node is None:
return
self.post_order(node.left_child)
self.post_order(node.right_child)
print(node.data, end=" ")
if __name__ == '__main__':
t = Tree()
for i in range(10):
t.add(i)
print("\n广度遍历:")
t.breadth_travel()
print("\n先序遍历:")
t.pre_order(t.root)
print('\n中序遍历:')
t.in_order(t.root)
print('\n后序遍历:')
t.post_order(t.root)
'''
广度遍历:
0 1 2 3 4 5 6 7 8 9
先序遍历:
0 1 3 7 8 4 9 2 5 6
中序遍历:
7 3 8 1 9 4 0 5 2 6
后序遍历:
7 8 3 9 4 1 5 6 2 0
'''
非递归 完成 树的所有遍历
class Node(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Tree(object):
def __init__(self, root=None):
self.root = root
def add(self, val):
node = Node(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def bre_order(self):
if self.root is None:
return None
queue = [self.root]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, end=" ")
if temp_node.left is not None:
queue.append(temp_node.left)
if temp_node.right is not None:
queue.append(temp_node.right)
def pre_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
print(temp_node.val, end=" ")
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
temp_node = node.right
def in_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack.pop()
print(node.val, end=" ")
temp_node = node.right
def post_order(self):
if self.root is None:
return None
stack = []
temp_node = self.root
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
node = stack[-1]
temp_node = node.right
if temp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
obj = Tree()
for i in range(1, 9):
obj.add(i)
obj.bre_order()
print()
obj.pre_order()
print()
obj.in_order()
print()
obj.post_order()
print()
'''
1 2 3 4 5 6 7 8
1 2 4 8 5 3 6 7
8 4 2 5 1 6 3 7
8 4 5 2 6 7 3 1
'''
全部传参 递归和非递归 混用 完成 树的所有遍历
class TreeNote(object):
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object):
def __init__(self):
self.root = None
def add(self, val):
node = TreeNote(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def bre_order(self, node):
if node is None:
return
queue = [node]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, end=" ")
if temp_node.left is not None:
queue.append(temp_node.left)
if temp_node.right is not None:
queue.append(temp_node.right)
def pre_order(self, node):
if node is None:
return
print(node.val, end=" ")
self.pre_order(node.left)
self.pre_order(node.right)
def in_order(self, node):
if node is None:
return
self.in_order(node.left)
print(node.val, end=" ")
self.in_order(node.right)
def post_order(self, node):
if node is None:
return None
stack = []
temp_node = node
while temp_node or stack:
while temp_node:
stack.append(temp_node)
temp_node = temp_node.left
left_node = stack[-1]
temp_node = left_node.right
if temp_node is None:
node = stack.pop()
print(node.val, end=" ")
while stack and node == stack[-1].right:
node = stack.pop()
print(node.val, end=" ")
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
print("\n广度遍历为:")
t.bre_order(t.root)
print("\n前序遍历为:")
t.pre_order(t.root)
print("\n中序遍历为:")
t.in_order(t.root)
print("\n后序遍历为:")
t.post_order(t.root)
'''
广度遍历为:
0 1 2 3 4 5 6 7 8 9
前序遍历为:
0 1 3 7 8 4 9 2 5 6
中序遍历为:
7 3 8 1 9 4 0 5 2 6
后序遍历为:
7 8 3 9 4 1 5 6 2 0
'''
- 总结:二叉树的遍历,有递归和非递归的完成方式;二叉树的添加结点和广度遍历都是使用队列来完成的,二叉树深度遍历的三种方式都是使用栈结构来完成的;递归方式遍历必须传参,而且传入的参数就是根结点;非递归方式的遍历可以传参也可以不传参,选择传的话,就是传入根结点,不传参是直接获取到构造方法中封装的根结点(类变量:根结点)