排序算法:快速排序、归并排序、计数排序详解
排序算法的算法常常是我们解决其他问题的第一步。对于面试来说,最常用的排序分为三种:快速排序、归并排序、计数排序。一般甚至要求在面试时手写出来。
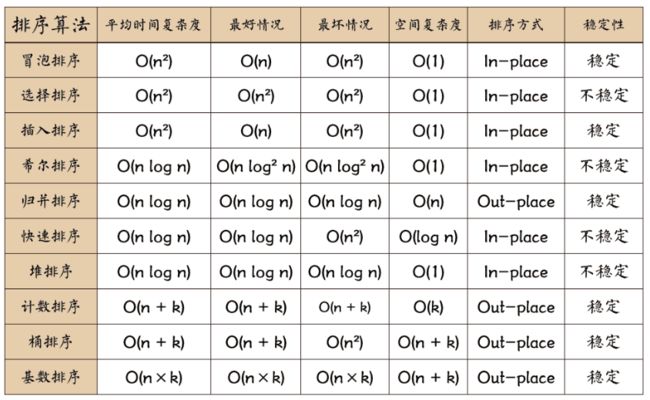
排序算法分为简单排序和先进排序,上面说的三种就是先进排序。先进排序的效率更高,但是也不是说,就不用学简单排序。在某些情况下简单排序更有效。
一、排序算法的约定
在学习具体的排序算法之前,为了使代码具有更好的可读性,需要做一些约定:
(1)假设要重新排列的数组都有一个主键(索引)。排序算法的目标就是将所有元素的主键(索引)按某种方式排列。例如,数字大小,字母顺序。
(2)我们将排序算法放在类的sort()方法中,不同的排序算法有不同的实现,例如Insertion.sort()、Merge.sort()、Quick. sort()等。
(3)还有两个辅助算法:less()方法对元素进行比较,exch()方法将元素交换位置。exch()方法的实现很简单,通过Comparable接口实现less()方法也不困难。
public class Example
{
public static void sort(Comparable[] a){
//排序算法的具体实现
}
private static boolean less(Comparable v, Comparable w){
return v.compateTo(w)<0;
}
private static void exch(Comparable[] a,int i, int j){
Comparable t=a[i];a[i]=a[j];a[j]=t;
}
public static boolean isSorted(Comparable[] a){//测试数组是否有序
for(int i=1;i<a.length;i++){
if(less(a[i],a[i-1])) return false;
}
}
}
一、先进排序
1.快速排序(quick sort)
快速排序的思想如下:
(1)选定一个中枢的值(pivot),然后对数组进行分区(partition),把数字比中枢值小的放左边,比中枢值大的放右边,结构成这样:{比中枢值小的数}中枢值{比中枢值大的数}
(2)继续将左子序列和右边子序列选取中枢值做排序,直到子序列只有一个数字为止
(3)若是左右序列都是排序好的,自然整个序列是排序号的序列
//伪代码
void 快速排序(数组,左侧序号,右侧序号)
{
分割数据,将left保存到i
快速排序(数组,原左侧序号,i-1)
快速排序(数组,i+1,原右侧序号)
}
//实现代码
public class Quick {
public int[] sort(int[] nums){
sort(nums, 0, nums.length-1);
return nums;
}
public void sort(int[] nums, int low, int high){
int pivot = partition(nums, low, high);//进行分区,并返回中枢值的位置
sort(nums,low,pivot-1);//左子序列
sort(nums,pivot+1,high);//右子序列
}
}
具体步骤
以严蔚敏的《数据结构》书上所示,步骤如下:
(1)选取数组中第一个值作为中枢值(pivot),并将其作为临时值temp存储起来
(2)首先判断高位的值,若比中枢镇大,则左移,若比中枢值小,则将当前高位的值赋给低位
(3)接着判断低位的值,若比中枢值小,则又移,若比中枢值大,则将当前低位的值赋给高位
(4)当两指针相等时,结束分区,将临时值temp赋给当前位置
public static void main(String[] args) {
int[] a = {49,38,65,97,76,13,27,49}; //数据源
sort(a,0,a.length-1);
System.out.println(Arrays.toString(a));
}
public static void sort(int[] a,int low ,int high){ //迭代
if(high<=low) return;
int pivot = partition(a,low,high); //进行分区,返回中心的位置
sort(a,low,pivot-1); //继续划分左序列
sort(a,pivot+1,high); //继续划分右序列
}
public static int partition(int[] a,int low ,int high){ //一次快排的划分
int pivot = a[low]; //先选取数组第一位作为中枢值,书上的做法是将0位用作辅助空间,数组大小是n+1,从1~n放置待排序元素
while(low<high){
while(low<high && a[high]>=pivot) high--; //高位左移寻找小于中心轴的值,结束循环
a[low] = a[high]; //将高位的值赋给低位
while (low<high && a[low]<=pivot) low++; //低位右移寻找大于中心轴的值,结束循环
a[high] = a[low]; //将低位的值赋给高位
}
a[low] = pivot ; //在中枢轴赋值之前第一位的值
return low; //要返回枢轴的位置,而不是a[low]的值
}
易犯错的地方
(1)判断条件a[high]>=temp或a[low]<=temp一定要记得等于号,也就是说相等的情况下,指针继续移动,不进行交换值
(2)双指针汇聚的时候,要记得将中枢值插入回中间的位置,即a[low] = temp
(3)要返回中枢值的位置,而不是中枢值,即return low;,而不是a[low]。这时low=high
分析
(1)为什么选取第一个数值作为中枢值?可以选其他值吗?第一个数值容易取得。也可以任意选其他值。
(2)选择第一个值之后,为什么首先移动高位指针?因为选第一个值之后,低位的位置就空出来了,需要从高位取数值填到低位
(3)为什么高位和低位的指针要交替移动?因为高位的数被赋值给低位后,高位的位置就空出来了,需要去移动低位指针。反之,亦然。
(4)高低位指针移动的本质是什么?实际上是将数值低的数放到左边,数值高的数放到右边,并不考虑左边或右边内部的排序如何。内部的排序将在下一次快速排序再进行整理。
算法改进
(1)对于小数组,快速排序比插入排序慢。在排序小数组时应该切换到插入排序
(2)使用子数组的一小部分元素的中位数来切分数组效果最好
(3)在拥有大量重复元素的数组中,快速排序算法仍然会将它且分为更小的数组。一种办法是将元素分为三部分:{小于}{等于}{大于}
总结
(1)快速排序是应用最广的排序算法,它流行的原因是当数据量n很大时,它是原地排序,只占用lgN的辅助栈空间,属于是O(nlogn)时间复杂度的先进排序。
(2)如果中枢值(pivot)选取不对,那么性能受到严重影响,时间复杂度劣化为O(n2)
特点:快速排序是对冒泡排序的改进,时间复杂度O(nlgn),最糟糕的情况下会降到O(n2)。平均时间在所有先进方法中属于最好的。
二、简单排序
1.插入排序
1.1 直接插入排序
//数据源
ints[] a = {49,38,65,97,76,13,27,49};
for(int i=1;i<a.length;i++){ //第一层循环,从第二位开始插入
if(a[i]<a[i-1]){ //只有第i位比前一位小时,才进行下列操作,否则忽略下述操作
int temp = a[i]; //将待比较的数存起来
int j =i; //将位置存起来用来迭代变化
while(j>0 && temp<a[j-1]){ //待比较的数比前一位小才能往前插入,同时不能越界
a[j] = a[j-1]; //记录的位置后移,将前一位的数值赋值给后一位
j--; //比较位置的指针前移
} //当待比较数大于或等于前一位时结束循环
a[j] = temp; // 将待比较数插入当前位置
}
}
特点:只需要一个记录的辅助空间,比较和移动平均需要n2/4,最糟情况下为n2/2,时间复杂度为O(n2)。当需要排序稳定,并且n规模不大时,优先选择此排序方法。
2.冒泡排序
int[] a = {49,38,65,97,76,13,27,49};
for(int i=0;i<a.length;i++){ //第一层循环
for(int j=1;j<a.length-i;j++){ //从第二位数开始比较
if(a[j]<a[j-1]){ //若当前数字比前一位小,则交换顺序
int temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
}
}
}
特点:比较和移动都是n(n-1)/2次,排序稳定,时间复杂度为O(n2)
3.选择排序
3.1简单选择排序
int[] a = {49,38,65,97,76,13,27,49};
for(int i=0;i<a.length;i++){ //遍历第一层循环
int p = i; //记录当前位置
for(int j=i+1;j<a.length;j++){
if(a[j]<a[p]){
p = j; //找出最小值所在位置
}
}
int temp = a[i];
a[i] = a[p];
a[p] = temp; //进行交换
}
特点:排序不稳定,每次只交换一次位置,最差情况需要移动3(n-1)次,但需要比较n(n-1)/2次关键字,所以还是O(n2)