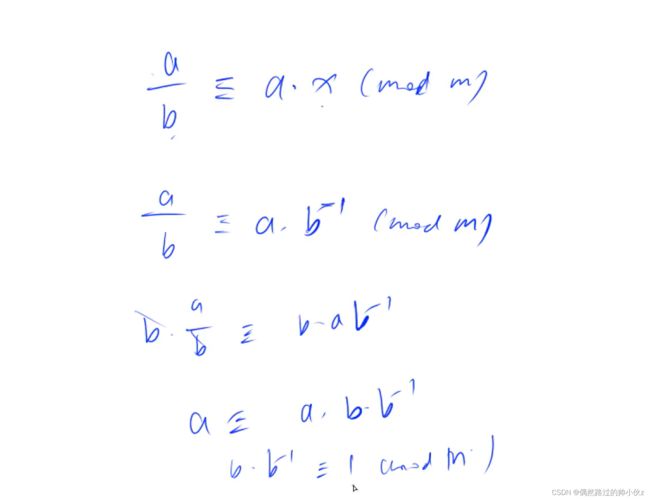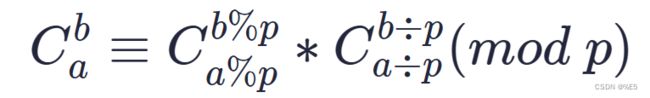偶然路过的帅小伙z
偶然路过的帅小伙z

acwing算法基础课-第四章 数学知识

数学知识

  • 质数
    • 试除法判定质数
      • 模板
      • AcWing 866 试除法判定质数（模板题）
    • 试除法分解质因数
      • 思想
      • 模板
      • AcWing 867 分解质因子（模板题）
    • 筛质数
      • 朴素筛法求素数（埃氏筛法）
        • 思想
        • 模板
        • AcWing 868 筛质数 （朴素筛法求素数）(埃氏筛法)（模板题）
      • 线性筛法求素数
        • 思想
        • 模板
        • AcWing 868 筛质数 （线性筛法求素数）（模板题）
  • 约数
    • 试除法求约数
      • 模板
      • AcWing 869 试除法求约数（模板题）
    • 求约数个数
      • 思想
      • AcWing 870 约数个数(模板题)
    • 求约数之和
      • 思想
      • AcWing 871 约数之和（模板题）
    • 最大公约数
      • 思想
      • 模板
      • AcWing 872 最大公约数（模板题）
  • 欧拉函数
    • 思想
    • 模板
    • AcWing 873 欧拉函数（模板题）
    • AcWing 874 筛法求欧拉函数.cpp（模板题）
  • 快速幂
    • 思想
    • 模板
    • AcWing 875 快速幂（模板题）
    • AcWing 876 快速幂求逆元
  • 扩展欧几里德算法
    • 思想
    • 模板
    • AcWing 877 扩展欧几里德算法（模板题）
    • AcWing 878 线性同余方程
  • 中国剩余定理
    • 思想
    • AcWing 204 表达整数的奇怪方式
  • 高斯消元
    • 思想
    • 模板
    • AxWing 883 高斯消元解线性方程组（模板题）
    • AcWing 884 高斯消元解异或线性方程组
  • 求组合数
    • 思想
    • 组合数 I
      • 模板
      • AcWing 885 求组合数 I（模板题）
    • 组合数 II
      • 模板
      • AcWing 886 求组合数 II（模板题）
    • 组合数 III
      • 思想
      • 模板
      • AcWing 887 球组合数 III（模板题）
    • 组合数 IV
      • 思想
      • 模板
      • AcWing 888 球组合数 IV（模板题）
    • 卡特兰问题
      • 思想
      • AcWing 889 满足条件的01序列（模板题）
  • 容斥原理
    • 思想
    • AcWing 890 能被整除的数
  • 博弈论
    • 思想
    • AcWing 891 Nim 游戏（Nim游戏 - 模板题）
    • AcWing 892 台阶-Nim游戏
    • AcWing 893 集合-Nim游戏（有向图游戏的和 - 模板题）
    • AcWing 894 拆分-Nim游戏

质数

试除法判定质数

模板

试除法判定质数 —— 模板题 AcWing 866. 试除法判定质数

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

AcWing 866 试除法判定质数（模板题）

对于 i <= x / i； 因为 x 的因子是成对出现的，当遍历到 i时，说明 2 ~ (i - 1) 无 x的因子。
遍历到 i时，如果 i 为大于sqrt(n)的因子，那么 x / i一定被遍历了，所以只需遍历到 sqrt(n)

#include
using namespace std;

int main()
{
	
	int n;
	cin >> n;
	while(n--)
	{
		int x;
		cin >> x;
		bool flag = true;
		if(x < 2)
		{
			printf("No\n");
			continue;
		}
		for(int i = 2; i <= x / i; i++)
		{
			if(x % i == 0)
			{
				flag = false;
				printf("No\n");
				break;
			}
		}
		if(flag) printf("Yes\n");
	}
	return 0;
 }

试除法分解质因数

思想

思路操作：对于待分解的正整数n：
1.从2开始，依次尝试将n除以小于等于sqrt(n)的每个素数。
2.如果某个素数p能够整除n，那么p就是n的一个质因子，记录下p后，继续对n/p执行分解操作。
3.如果没有小于等于sqrt(n)的素数能够整除n，那么n本身就是质数，分解结束。
注意，为了提高效率，我们在试除时只需要考虑小于等于sqrt(n)的素数是否能够整除n，因为如果n有大于sqrt(n)的质因数，它们的积一定大于n，不可能整除n。

模板

试除法分解质因数 —— 模板题 AcWing 867. 分解质因数

void divide(int x) 
{
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            int s = 0;
            while (x % i == 0) x /= i, s ++ ;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;
    cout << endl;
}

AcWing 867 分解质因子（模板题）

//对于 i <= x / i； 因为 x 的质因子是成对出现的，
//当遍历到 i时，说明 2 ~ (i - 1) 无 x的质因子
//遍历到 i时，如果 i 为大于sqrt(n)的质因数，那么 x / i一定被遍历了，所以只需遍历到 sqrt(n)

#include
using namespace std;
void divide(int x)
{
	for(int i = 2; i <= x / i; i++)
	{
		if(x % i == 0)
		{
			int s = 0;
			while(x % i == 0)
			{
				x /= i;
				s++;
			}
			printf("%d %d\n", i, s);
		}
	 }
//x 中最多只包含一个大于sqrt(n)的质因子，如果有的话，单独处理 
	if(x > 1) printf("%d 1\n\n", x);

}
int main()
{
	int n ;
	cin >> n;
	while(n--)
	{
		int x;
		cin >> x;
		divide(x);
	}
	return 0;
  }

筛质数

朴素筛法求素数（埃氏筛法）

思想

操作步骤：
1.从2开始，将2标记为素数。
2.将所有2的倍数标记为合数。
3.找到下一个未被标记的数，将其标记为素数。
4.将该素数的所有倍数标记为合数。
5.重复步骤3和4，直到找不到新的素数。
实际上，为了提高效率，我们只需遍历到 sqrt(n) 就可以找到2~n之间所有的素数。
时间复杂度为O(nloglogn)。

模板
朴素筛法求素数 —— 模板题 AcWing 868. 筛质数
int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i; j <= n; j += i)
            st[j] = true;
    }
}
AcWing 868 筛质数 （朴素筛法求素数）(埃氏筛法)（模板题）
#include
using namespace std;
#define N 1000010 
bool st[N];
int cnt;
int primers[N];
int n;

void get_primers(int n)
{
	for(int i = 2; i <= n; i++)
	{
		if(!st[i])
		{
			primers[cnt++] = i;
			for(int j = i; j <= n; j += i)  st[j] = true;
		}
	}
//for(int j = i; j <= n; j += i)  st[j] = true;
//该语句放这的话，没必要，时间复杂度高
//我们只需筛质数的倍数就行
//因为当 i 为合数时，因为 2 ~ (n - 1)有 i的质因子，所以已经被筛了 
}
int main()
{
	cin >> n;
	get_primers(n);
	cout << cnt <<endl;
	return 0;
 }

线性筛法求素数

思想

线性筛法是一种高效的求素数的方法，可以在可以在O(n)的时间内找到从1到n之间的所有素数。
操作步骤：
1.定义一个布尔数组isprime,将数组中的所有元素初始化为true.
2.定义一个数组primers,用于存储找到的素数。初始化primers为空.
3.从2开始遍历到n, 对于每个数 i, 执行以下操作：
（1）.如果isprime为true,将 i 加入primes数组
（2）.遍历primes数组每个素数p,如果p * i > n,，跳出循环。否则，将 p * i标记为合数，即isprimer[p * i] = false如果 p 能整除 i,跳出循环
4.遍历完 2 ~ n的元素后，isprimer数组中下标为true的下标就是素数。
线性筛法不仅能够快速地找到素数，还可以记录每个合数的最小质因子。具体地说，在执行第3步时，如果如果 p 能整除 i,则停止处理，因为 p 已经是 i 的的最小质因子了。

对于3.(2)（同模板内容） 的解析
核心：n 只会被最小质因子筛掉。

  1. st[primes[j] * i] = true.
    对于一个合数 x, 设pj为 x 的最小质因子，当 i 枚举到 x/pj 时，便会被筛除，例， x = 8, i = 8/2 = 4 时，st[pj * i] = true.
    ，每次用最小质因子去筛，而合数的最小质因子都是唯一的，所以每个数只会被筛一次，所以它是线性的。
  2. if (i % primes[j] == 0) break；i % primes[j] 有两种可能性
    a. i % pj == 0, pj是 i 的最小质因子， pj 一定是pi * i 的最小质因子
    b. i % pj != 0, pj 小于 i的所有质因子， pj 一定是pi * i 的最小质因子
  3. for (int j = 0; primes[j] <= n / i; j ++ )
    在判断语句中 加入 && j < cnt 没必要
    a. i 为合数时， 因为 i 的最小质因子小于 i, 且 i的最小质因子在primers[cnt]中，当 枚举到 i的最小质因子便会停下来。
    b. i 为质数，在这步中if (!st[i]) primes[cnt ++ ] = i;i会被收进primers[cnt]中，
    当primer[j] = i 时, 便会停下来。也符合条件。

模拟一下 2 ~ 15,便会清楚很多

i 被筛 p[cnt++] cnt
2 2 * 2 p[0] = 2 1
3 2 * 3 ，3 * 3 p[1] = 3 2
4 2 * 4
5 2 * 5，3 * 5 p[2] = 5 3
6 2 * 6
7 2 * 7 p[3] = 7 4
…… …… …… ……
模板

线性筛法求素数 —— 模板题 AcWing 868. 筛质数

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
AcWing 868 筛质数 （线性筛法求素数）（模板题）

线性筛法求素数 常用该法
当 n 为 10 ^ 6时，与 朴素法差不多；n 为 10 ^ 7时, 比朴素法快一倍

#include
using namespace std;
#define N 1000010 
bool st[N];
int cnt;
int primers[N];
int n;

void get_primers(int n)
{
	for(int i = 2; i <= n; i++)
	{
		if(!st[i])	primers[cnt++] = i;
		for(int j = 0; primers[j] <= n / i; j++)
		{
			st[primers[j] * i] = true;
			if(i % primers[j] == 0) break;
		}
	}
}
int main()
{
	cin >> n;
	get_primers(n);
	cout << cnt <<endl;
	return 0;
 }

约数

试除法求约数

模板

试除法求所有约数 —— 模板题 AcWing 869. 试除法求约数

vector<int> get_divisors(int x)
{
    vector<int> res;
    for (int i = 1; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);
        }
    sort(res.begin(), res.end());
    return res;
}

AcWing 869 试除法求约数（模板题）

#include
#include
#include
using namespace std;

vector<int> get_divisors(int x)
{
	vector<int> res;
	for(int i = 1; i <= x / i; i++)
	{
		if(x % i == 0) 
		{
			res.push_back(i);
			if(i != x / i) res.push_back(x / i);
		}
	}
	sort(res.begin(), res.end());
	return res;
 } 
int main()
{
	int n;
	cin >> n;
	while(n--)
	{
		int x;
		cin >> x;
		auto res = get_divisors(x);
		for(auto t : res) printf("%d ", t);
		puts(""); 
		res.clear();
	}
	
	return 0;
 }

求约数个数

思想

一般地，对自然数n进行分解质因数，设n可以分解为
n=p⑴α⑴·p⑵α⑵·…·p(k)^α（k)
其中p⑴、p⑵、…p(k）是不同的质数，α⑴、α⑵、…α（k）是正整数，则形如
n=p⑴β⑴·p⑵β⑵·…·p(k)^β（k)的数都是n的约数，其中β⑴可取a⑴+1个值：0,1,2，…，α⑴；β⑵可取α⑵+1个值：0,1,2，…，α⑵…；β（k）可取a(k)+1个值：0,1,2，…，α（k).且n的约数也都是上述形式，根据乘法原理，n的约数共有
（α⑴+1）（α⑵+1）…（α（k)+1） ⑺个。

公式：
如果 N = p1^c1 * p2^c2 * ... *pk^ck; 约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)

例：n = 8, 8 = 2a1 * 3a2，a1=3,a2=1
则约数 x = 2b13b2;
b1可取（0，1，2，3）
b2可取（0，1）
共有（a1 + 1）*（a2 + 1）种匹配结果，即 x的结果共有 8种

AcWing 870 约数个数(模板题)

#include
#include
#include
using namespace std; 
const int N = 1e9 + 7;
int n;

unordered_map<int, int> primes;
int main()
{
	cin >> n;
	while(n--)
	{
		int x;
		scanf("%d", &x);
		for(int i = 2; i <= x / i; i++)
		{
			if(x % i == 0)
			{
				while(x % i == 0)
				{
					x /= i;
					primes[i]++;
				}
			}
		}
		if(x > 1) primes[x]++;
	}
	long long res = 1;
	for(auto t : primes)
	{
		res = res * (t.second + 1) % N;
	}
	printf("%lld\n", res);
	
	return 0;
 }

求约数之和

思想

公式
如果 N = p1^c1 * p2^c2 * ... *pk^ck； 约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

例：24 = 23 * 31, 约数m = 2b1 * 3b2，b1={0，1，2，3}，b2={0，1}；
s = 20*31 + 21*31 + 22*31 + 23*31 + 20*30 + 21*30 + 22*30 + 23*30
s = (20 + 21 + 22 + 23) * (30 + 31),也就是上面的合并

AcWing 871 约数之和（模板题）

#include
#include
#include
using namespace std; 
const int N = 1e9 + 7;
int n;

unordered_map<int, int> primes;
int main()
{
	cin >> n;
	while(n--)
	{
		int x;
		scanf("%d", &x);
		for(int i = 2; i <= x / i; i++)
		{
			if(x % i == 0)
			{
				while(x % i == 0)
				{
					x /= i;
					primes[i]++;
				}
			}
		}
		if(x > 1) primes[x]++;
	}
	long long res = 1;
	for(auto t : primes)
	{
		long long t1 = 1;
		int a = t.first, b = t.second; 
		while(b--)  t1 = (t1 * a + 1) % N;// 循环结束后，t1=(px^0 + px^1 + ... + px^cx)
		res = res * t1 % N;
	}
	printf("%lld\n", res);
	
	return 0;
 }

最大公约数

思想

这里用欧几里得算法求
欧几里得算法又称辗转相除法，是指用于计算两个非负整数a，b的最大公约数。应用领域有数学和计算机两个方面。计算公式gcd(a,b) = gcd(b,a mod b)。
证明

让D 表示 a 与 b 的公约数集合，Q 表示 b 与 a % b 的公约数集合
因为a / b = k(余r)所以 a可以表示成a = kb + r（a，b，k，r皆为正整数，且r 假设d是a,b的任意一个公约数，则 a%d == 0, b%d == 0
而r = a - kb，两边同时除以d，r/d=a/d-kb/d=m，由等式右边可知m为整数，因此r%d==0
而r=a mod b,因此d也是b,a mod b的公约数(暂时认为D⊆R)
假设q是b,a mod b的公约数, 则b%q == 0,(a-kb)%q == 0
(a − k ∗ b a-kba−k∗b)%q = a%d-k∗ *∗b%q == 0 , k是一个整数。
进而a%q == 0.因此q也是a,b的公约数(暂时认为R⊆D)
由上可知，D=R，因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证。
转载修改于辜月博客

模板

欧几里得算法 —— 模板题 AcWing 872. 最大公约数

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

AcWing 872 最大公约数（模板题）

#include 
using namespace std;

int gcd(int a,int b)
{
	return b ? gcd(b, a % b) : a;
}

int main()
{
	int n;
	scanf("%d", &n);
	while(n--)
	{
		int a, b;
		scanf("%d%d", &a, &b);
		printf("%d\n", gcd(a, b));
	}
	
	
	return 0;
}

欧拉函数

思想

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目.

acwing算法基础课-第四章 数学知识_第1张图片
证明：可参考这位博主的证明,通俗易懂
糖豆爸爸

模板

求欧拉函数 —— 模板题 AcWing 873. 欧拉函数

int phi(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);

    return res;
}

筛法求欧拉函数 —— 模板题 AcWing 874. 筛法求欧拉函数

int primes[N], cnt;     // primes[]存储所有素数
int euler[N];           // 存储每个数的欧拉函数
bool st[N];         // st[x]存储x是否被筛掉


void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];
                break;
            }
            euler[t] = euler[i] * (primes[j] - 1);
        }
    }
}

AcWing 873 欧拉函数（模板题）

#include
using namespace std;

int phi(int x)
{
	int res = x;
	for(int i = 2; i <= x / 2; i++)	
	{
		if(x % i == 0)
		{
			res = res / i * (i - 1);
			while(x % i == 0) x /= i; 
		}
	}
	if(x > 1) res = res / x * (x - 1);	
	return res;
}

int main()
{
	int n;
	cin >> n;
	
	while(n--)
	{
		int x;
		cin >> x;
		cout << phi(x) <<endl;
	 } 
	
	return 0;
  }

AcWing 874 筛法求欧拉函数.cpp（模板题）

#include
using namespace std;
const int N = 1e6 + 7;

int primers[N];
int cnt;
bool st[N];
int eular[N];
long long res;

void get_eulars(int n)
{
	eular[1] = 1;
	for(int i = 2; i <= n; i++)
	{
		if(!st[i])
		{
			primers[cnt++] = i;
			eular[i] = i - 1;//质数i的欧拉函数值是eular[i]=i−1
		}
		for(int j = 0; primers[j] <= n / i; j++)
		{
			int t = primers[j] * i;
			st[t] = true;
			if(i % primers[j] == 0)
			{
//primers[j]为 i 的质因子，eular[i * primers[j]]就是 多乘了一个 primers[j]
				eular[i * primers[j]] = eular[i] * primers[j];
				break;
			}
//primers[j]不是 i 的质因子，展开就能发现规律
//eular[i * primers[j]] = primers[j] * eular[i] *（1 - 1/primers[j] ）
			eular[i * primers[j]] = eular[i] * (primers[j] - 1);
		}
		
	}
}

int main()
{
	int n;
	cin >> n;
	get_eulars(n);
	for(int i = 1; i <= n; i++) res += eular[i];
	cout << res <<endl;
	return 0;
}

快速幂

思想

快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。
以下以求a的b次方来介绍
把b转换成二进制数。
该二进制数第i位的权为 2i-1
例如 a11 = a2的0次方+2的1次方+2的3次方
11的二进制是1011 ，
11 = 23 * 1 + 22 * 0 + 21 * 1+20 * 1
因此，我们将a¹¹转化为计算 a2的0次方 * a2的1次方 * a2的3次方

这种思想是将指数 十进制与二进制转换

快速幂可以用位运算来实现，因为只需计算指数二进制的位数，所以其时间复杂度为其时间复杂度为 O(log₂N)

模板

快速幂 —— 模板题 AcWing 875. 快速幂
求 m^k mod p，时间复杂度 O(logk)。

int qmi(int m, int k, int p)
{
    int res = 1 % p, t = m;
    while (k)
    {
        if (k&1) res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}

AcWing 875 快速幂（模板题）

#include
using namespace std;

long long qmi(long long a, long long b, long long p)
{
	long long res = 1 % p, t = a;
	while(b)
	{
		if(b & 1) res = res * t % p;// 如果指数最低位为 1  
		t = t * t % p;  
		b >>= 1; //指数右移 
	}
	return res;
}

int main()
{
	int n;
	scanf("%d", &n);
	while(n--)
	{
		long long a, b, p;
		scanf("%lld%lld%lld", &a, &b, &p);
		printf("%lld\n", qmi(a, b, p));
	}
	return 0;
 }

AcWing 876 快速幂求逆元

在这里插入图片描述
注意b 与 m互质，图片来自acwing
acwing算法基础课-第四章 数学知识_第2张图片

费马小定理(Fermat’s little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有a（p-1）≡1（mod p）。

a（p-1）≡1（mod p）,a与p互质，且q为质数
a * a（p-2） ≡1（mod p）;
则 a（p-2） 为 a 的逆元

#include
using namespace std;

long long qmi(long long a, long long b, long long p)
{
	long long res = 1 % p, t = a;
	while(b)
	{
		if(b & 1) res = res * t % p;
		t = t * t % p;
		b >>= 1;
	}
	return res;
}

int main()
{
	int n;
	scanf("%d", &n);
	while(n--)
	{
		long long a, p;
		scanf("%lld%lld", &a, &p);
		if(a % p != 0)
		printf("%lld\n", qmi(a, p - 2, p));
		else
		printf("impossible\n");
	}
	return 0;
 }

扩展欧几里德算法

思想

相关证明可以参考该博主，非常详细（包含扩展欧几里得算法的推导过程，裴蜀定理， 扩展欧几里得算法，线性同余方程）
蒟蒻豆进阶之路

模板

扩展欧几里得算法 —— 模板题 AcWing 877. 扩展欧几里得算法，
求x, y，使得ax + by = gcd(a, b)

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a/b) * x;
    return d;
}

AcWing 877 扩展欧几里德算法（模板题）

#include 
using namespace std;


int exgcd(int a, int b, int &x, int &y)
{
	if(!b)
	{
		x = 1; y = 0;
		return a;
	}
	int d = exgcd(b, a % b, y, x);
	y -= (a / b) * x;
	return d;
}
int main()
{
	int n; 
	scanf("%d", &n);
	while(n--)
	{
		int a, b, x, y;
		scanf("%d%d", &a, &b);
		exgcd(a, b, x, y);
		printf("%d %d\n", x, y);
	}
	return 0;
}

AcWing 878 线性同余方程

#include
using namespace std;


int exgcd(int a, int b, int &x, int &y)
{
	if(!b)
	{
		x = 1; y = 0;
		return a;
	}
	int d = exgcd(b, a % b, y, x);
	y -= (a / b) * x;
	return d;
}
int main()
{
	int n;
	scanf("%d", &n);
	while(n--)
	{
		
		int a, b, m, x, y;
		scanf("%d%d%d", &a, &b, &m);
		int d = exgcd(a, m, x, y);
		if(b % d == 0) //判断b是不是d的倍数 
		{
			// x 乘以 b是d的多少倍 
			printf("%d\n", (long long) b /d * x % m);
		}
		else
		printf("impossible\n");
	}
	
	
	return 0;
 }

中国剩余定理

思想

百度百科的证明不错，
中国剩余定理（孙子定理）

关于百度百科的证明过程中该语句的解释：另外，假设x1 和 x2都是方程组(S) 的解，那么对于i(1,2,……n), x1 - x2 ≡ 0 (mod mi)。
x ≡ a1 (mod m1)
x ≡ a2 (mod m2)
…
x ≡ an (mod mn)
那么可以得到：
x1 ≡ a1 (mod m1)
x1 ≡ a2 (mod m2)
…
x1 ≡ an (mod mn)
x2 ≡ a1 (mod m1)
x2 ≡ a2 (mod m2)
…
x2 ≡ an (mod mn)，
由x1 - x2 ≡ 0 (mod mi)可知，（x1 - x2）% mi = 0 -->（x1%mi - x2%mi）% mi =0,因为 x1%mi = x2%mi，即得证。

对于本题，ai与mi不两两互质，也就不符合孙子定理，也就是说，我们需要重新推。
还是来看看这位大神的推导吧，
蒟蒻豆进阶之路

AcWing 204 表达整数的奇怪方式

#include
#include
using namespace std;

long long exgcd(long long a, long long b, long long &x, long long &y)
{
	if(!b)
	{
		x = 1; y = 0;
		return a;
	}
	long long d = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return d;
}

int main()
{
	int n;
	scanf("%d", &n);
	n--;
	long long a1, m1;
	cin >> a1 >> m1;
	while(n--)
	{
		long long a2, m2, k1, k2;
		scanf("%lld%lld", &a2, &m2);
		long long d = exgcd(a1, -a2, k1, k2);
		if((m2 - m1) % d)
		{
			cout << -1 <<endl;
			return 0;
		} 
		//此时 a1*k1+(-a2)*k2=m2-m1

		 k1 *= (m2 - m1) /d; // k1 变为(m2-m1)/d倍
		 
		 long long t = abs(a2 / d);
		 k1 = (k1 % t + t) % t;//k的最小正整数解 
		 
		 m1 = k1 * a1 + m1;
		 a1 = abs(a2 / d * a1);
	}
	long long x = (m1 % a1 + a1) %a1; //最小整数解
	printf("%lld\n", x);
	return 0;
 }

高斯消元

思想

定义简介：数学上，高斯消元法（或译：高斯消去法），是线性代数规划中的一个算法，可用来为线性方程组求解。但其算法十分复杂，不常用于加减消元法，求出矩阵的秩，以及求出可逆方阵的逆矩阵。不过，如果有过百万条等式时，这个算法会十分省时。一些极大的方程组通常会用迭代法以及花式消元来解决。当用于一个矩阵时，高斯消元法会产生出一个“行梯阵式”。高斯消元法可以用在电脑中来解决数千条等式及未知数。亦有一些方法特地用来解决一些有特别排列的系数的方程组。
内容：消元法是将方程组中的一方程的未知数用含有另一未知数的代数式表示，并将其代入到另一方程中，这就消去了一未知数，得到一解；或将方程组中的一方程倍乘某个常数加到另外一方程中去，也可达到消去一未知数的目的。消元法主要用于二元一次方程组的求解。

核心：
初等行列变换

  1. 两方程互换，解不变；
  2. 一方程乘以非零数k，解不变；
  3. 一方程乘以数k加上另一方程，解不变。

增广矩阵 -> 阶梯矩阵
转换过程即 高斯消元法
对于 高斯消元解线性方程组，可以参考该博主的文章
糖豆爸爸

高斯消元步骤：
依次枚举增广矩阵的列
（1）找到该列绝对值最大的行
（2）将该行换到（未确定阶梯型的行的）最上面
（3）将该行第一个数（当前枚举的列）变成1（该行其它数作相应变换）
（4）将该行下面所有行的当前列消成0，（该行其它数作相应变换）

（枚举完即是阶梯矩阵）
（5）如果该矩阵是唯一的解，则,从最后一行开始依次往上倒，每次将该行上面的数全变成 0，那么当前行只有一个 1，该 1对应的未知数即为第 i 行关于第 i 个未知数的解

方程组有三种情况，即有唯一解，无穷多的解，无解

唯一解：完美阶梯形
acwing算法基础课-第四章 数学知识_第3张图片
无解：0 = 非0，即 存在某一行系数都为 0，该方程等号右侧的常数不为0。（原方程中出现了矛盾）

无穷多的解：0 = 0，即 存在某一行系数都为 0，该方程等号右侧的常数也为0。（原方程中出现了一样的方程）

模板

高斯消元 —— 模板题 AcWing 883. 高斯消元解线性方程组
a[N][N]是增广矩阵

int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )   // 找到绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);      // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];      // 将当前上的首位变成1
        for (int i = r + 1; i < n; i ++ )       // 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // 无解
        return 1; // 有无穷多组解
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    return 0; // 有唯一解
}

AxWing 883 高斯消元解线性方程组（模板题）

对于该代码的相关解答

if(r < n)
	{
		for(int i = r; i < n; i++)
			if(fabs(a[i][c]) > eps) return 2;//无解 
		return 1;// 无穷多的解
	}

1.为什么从第 r 行开始？

首先 r < n, 这意味着已经是无解或无穷多的解的情况，
而 r < n, 是因为在依次枚举增广矩阵的列时，出现了该列绝对值最大值都为 0的情况，这时continue, 即行不变，列加 1，说明有一个方程组出错了 。最后经过一系列操作转化成阶梯矩阵后，从第 r 行开始，方程左边系数都为 0，从这开始判断方程是 无解 还是 无穷多的解

2.判断无解情况，为什么要循环判断？

因为只要出现了 0 = 非0，即无解的情况
而无穷多的解需都满足 0 = 0

对于对于该代码的解答

//从最后一行开始往上消元计算 (不懂该语句的模拟一遍基本就ok了) 
	for(int i = n - 1; i >= 0; i--)
		for(int j = i + 1; j < n; j++)
			a[i][n] -= a[i][j] * a[j][n];

对于求最终未知数的值，只需a[i][n] -= a[i][j] * a[j][n]。
我们的目的是求a[i][n]，而除了 a[i][i]和 a[i][n]的元素外，我们不用第 i 行每个元素都减去 k（a[i][j]） * 对应 j 行元素。因为我们使用一次它（即 作为 k的元素）后，把它当作 0，便不再使用它了，不用管它（实际上应该为0，因为 第 i 行实际上是个方程，用了该 k 后，即消去了该未知数）

#include
#include
#include
using namespace std;
const int N = 110;
#define eps 1e-6
double a[N][N];
int n;
int gauss()
{
	int r, c;//r为当前行，c为列 
	for(c = 0, r = 0; c < n; c++)
	{
	//找 c列中绝对值最大的行 
		int t = r;
		for(int i = r + 1; i < n; i++)
			if(fabs(a[i][c]) > fabs(a[t][c])) 
				t = i;
	//说明出现了无解或无穷多的解情况	
		if(fabs(a[t][c]) < eps) continue;
	//交换，将绝对值最大的行放到第 c行 
		for(int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
	//将第 r行第 c列变成 1 
		for(int i = n; i >= c; i--) a[r][i] /= a[r][c];
	//将第 r行第 c列下面的列变成 0 
		for(int i = r + 1; i < n; i++)
			if(fabs(a[i][c]) > eps)
				for(int j = n; j >= c; j--)
					a[i][j] -= a[r][j] * a[i][c];
		r++;
	}
	if(r < n)
	{
		for(int i = r; i < n; i++)
			if(fabs(a[i][c]) > eps) return 2;//无解 
		return 1;// 无穷多的解
	}
	//从最后一行开始往上消元计算 (不懂该语句的模拟一遍基本就ok了) 
	for(int i = n - 1; i >= 0; i--)
		for(int j = i + 1; j < n; j++)
			a[i][n] -= a[i][j] * a[j][n];
	return 0;
}

int main()
{
	cin >> n;
	for(int i = 0; i < n; i++)
		for(int j = 0; j <= n; j++)
		scanf("%lf", &a[i][j]);
	int k = gauss();
	if(k == 0)
	{
		for(int i = 0; i < n; i++)
		{ 
			if(fabs(a[i][n]) < eps) a[i][n] = 0;
			printf("%.2f\n", a[i][n]);
		}
	}
	else if(k == 2)
		puts("No solution");
	else
	puts("Infinite group solutions");
	
	
	return 0;
 }

AcWing 884 高斯消元解异或线性方程组

等式与等式间的异或要左右两端全都异或才能保证等式左右两边依然相等
a ^ b ^ c = x；d ^ f= y
则 a ^ b ^ c ^ d ^ f = x ^ y

#include 
#include
using namespace std;
#define N 110

int a[N][N];
int n;

int gauss()
{
	int c, r;
	for(c = 0, r = 0; c < n; c++)
	{
	//从第 i 行往下，找第 1个 c列元素为 1的行 
		int t = r;
		for(int i = r; i < n; i++)
			if(a[i][c])
			{
				t = i;
				break;
			}
		
		if(!a[t][c]) continue;
		//交换 
		if(t != r) swap(a[t], a[r]);
		//消 0处理 
		for(int i = r + 1; i < n; i++)
			if(a[i][c])
				for(int j = n; j >= c; j--)
					a[i][j] ^= a[r][j]; //注意该操作 
		r++; 
	}
	if(r < n)
	{
		for(int i = r; i < n; i++)
			if(a[i][n])
			{
				puts("No solution");
				exit(0);
			}
		puts("Multiple sets of solutions");
		exit(0);
	}
	for(int i = n - 1; i >= 0; i--)
		for(int j = i + 1; j < n; j++)
			a[i][n] ^= a[j][n] * a[i][j]; //注意该操作
	return 0;
}

int main()
{
	cin >> n;
	for(int i = 0; i < n; i++)
		for(int j = 0; j <= n; j++)
			scanf("%d", &a[i][j]);
	gauss();
	for(int i = 0; i < n; i++) printf("%d\n", a[i][n]);
	
	
	return 0;
}

求组合数

思想

Cba

组合数 I : 适合 a, b 在 1 ~ 2000内的大小，有取模
组合数 II : 适合 a, b 在 1 ~ 1e5 内的大小，有取模
组合数 III : a, b 在 1 ~ 1e18内，适合 a, b 很大，取模（p) 很小的情况
组合数 IV : 无取模

组合数 I

核心：Cba=Cba−1+Cb−1a−1

模板

递归法求组合数 —— 模板题 AcWing 885. 求组合数 I

// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) c[i][j] = 1;
        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

AcWing 885 求组合数 I（模板题）

#include
using namespace std;
#define N 2010
const int eps = 1e9 + 7;

int c[N][N];
int main()
{
	int n;
	cin >> n;
	for(int i = 0; i <= N; i++)
		for(int j = 0; j <= i; j++)
			if(!j) c[i][j] = 1;
			else
				c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % eps;
	while(n--)
	{
		int a, b;
		cin >> a >> b;
		cout << c[a][b] << endl;
	}
	
	return 0;
}

组合数 II

Cba = (fact[a]∗infact[a−b]∗infact[b])

模板

通过预处理逆元的方式求组合数 —— 模板题 AcWing 886. 求组合数 II
首先预处理出所有阶乘取模的余数fact[N]，以及所有阶乘取模的逆元infact[N]
如果取模的数是质数，可以用费马小定理求逆元

int qmi(int a, int k, int p)    // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
    fact[i] = (LL)fact[i - 1] * i % mod;
    infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}

AcWing 886 求组合数 II（模板题）

#include
using namespace std;
const int N = 100010;
const int eps = 1e9 + 7;
int fact[N];   
int infact[N]; //逆元 

int qmi(int a, int b, int p) //快速幂，注意取模 
{
	int res = 1;
	while(b)
	{
		if(b&1) res = (long long)res * a % p;
		a = (long long)a * a % p;
		b >>= 1;
	}
	return res;
}
int main()
{
	int n;
	cin >> n;
	fact[0] = infact[0] = 1; //预处理 
	for(int i = 1; i < N; i++)
	{
		fact[i] =(long long)fact[i - 1] * i % eps;
		infact[i] =(long long)infact[i - 1] * qmi(i, eps - 2, eps) % eps;
	}
	while(n--)
	{
		int a, b;
		scanf("%d%d", &a, &b);
	//注意两次取模的位置 
		printf("%d\n", (long long)fact[a] * infact[b] % eps* infact[a - b] % eps);
	}
	
	return 0;
 }

组合数 III

思想

lucas定理
在这里插入图片描述

证明所需要的知识点
1.
acwing算法基础课-第四章 数学知识_第4张图片2.
acwing算法基础课-第四章 数学知识_第5张图片
3.
在这里插入图片描述
证明：推荐百度百科和维基百科
百度百科
维基百科
以下是维基百科的证明
acwing算法基础课-第四章 数学知识_第6张图片
acwing算法基础课-第四章 数学知识_第7张图片

模板

Lucas定理 —— 模板题 AcWing 887. 求组合数 III
若p是质数，则对于任意整数 1 <= m <= n，有：
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)


int qmi(int a, int k)       // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b)     // 通过定理求组合数C(a, b)
{
    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2) % p;
    }
    return res;
}


int lucas(LL a, LL b)
{
    if (a < p && b < p) return C(a, b);
    return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}

AcWing 887 球组合数 III（模板题）

#include
using namespace std;
typedef long long LL;
int p;

int qmi(int a, int b)
{
	int res = 1;
	while(b)
	{
		if(b&1) res = (LL)res * a % p;
		a = (LL)a * a % p;
		b >>= 1;
	}
	return res;
}
int C(int a, int b)
{
	if(b > a) return 0; //特殊化处理 
	int res = 1;
    //a(a-1)(a-2)……(a-b+1)与 1*2*3……*b都是 b次 
	for(int i = a, j = 1; j <= b; j++, i-- )
	{
		res = (LL)res * i % p;
		res = (LL)res * qmi(j, p - 2) % p;  
	}
	return res;
}
int lucas(LL a, LL b) //调用lucas公式 
{
	if(a < p && b < p) return C(a, b);
	return (LL)C(a%p, b%p) * lucas(a/p, b/p) % p; 
}

int main()
{
	int n;
	cin >> n;
	while(n--)
	{
		long long a, b;
		scanf("%lld%lld%d", &a, &b, &p);
		printf("%d\n", lucas(a, b));
	}
	return 0;
 }

组合数 IV

思想

算术基本定理: Cba=pα11 × pα22 × pα33 …… × pαkk

求n!中质因子p的个数：res = [n/p] + [n/(p2)] + [n/(p3)] + ……
简单证明：acwing算法基础课-第四章 数学知识_第8张图片

步骤：
(1). 筛素数，把 所需区间的的素数筛出来
(2). 计算Cba中每个已求得素数的个数
(3). 利用高精度乘法，计算Cba=pα11 × pα22 × pα33 …… × pαkk

模板

分解质因数法求组合数 —— 模板题 AcWing 888. 求组合数 IV
当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + …
3. 用高精度乘法将所有质因子相乘

int primes[N], cnt;     // 存储所有质数
int sum[N];     // 存储每个质数的次数
bool st[N];     // 存储每个数是否已被筛掉


void get_primes(int n)      // 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // 求n！中 p的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }

    return c;
}

get_primes(a);  // 预处理范围内的所有质数

for (int i = 0; i < cnt; i ++ )     // 求每个质因数的次数
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // 用高精度乘法将所有质因子相乘
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

AcWing 888 球组合数 IV（模板题）

#include
#include
using namespace std;
const int N = 5010;

int primers[N], cnt;
int sum[N];
bool st[N]; 

void get_primers(int a) //欧拉筛 
{
	for(int i = 2; i <= a; i++)
	{
		if(!st[i]) primers[cnt++] = i;
		for(int j = 0; primers[j] <= a / i; j++)
		{
			st[primers[j] * i] = true;
			if(i % primers[j] == 0) break;
		}
	}
}

int get(int n, int p) //求 n! 中质因子 p 的个数 
{
	int t = 0;
	while(n)
	{
		t += n / p;
		n /= p;
	}
	return t;
}
vector<int> mul(vector<int> a, int b) // 高精度乘低精度 
{
	vector<int> c;
	int t = 0;
	for(int i = 0; i < a.size(); i++)
	{
		t += a[i] * b;
		c.push_back(t%10);
		t /= 10;
	}
	while(t)
	{
		c.push_back(t%10);
		t /= 10;
	}
	return c;
}

int main()
{
	int a, b;
	scanf("%d%d", &a, &b);
	//欧拉筛
	get_primers(a);
	//依次枚举 a的质因子次数 
	for(int i = 0; i < cnt; i++)
	{
		int p = primers[i];
	//分母 p的出现的次数减去分子 p的出现的次数 
		sum[i] = get(a, p) - get(b, p) - get(a - b, p);
	}
	//求最终答案 
	vector<int> res;
	res.push_back(1);
	for(int i = 0; i < cnt; i++)//枚举每个质因子 
		for(int j = 0; j < sum[i]; j++)//迭代该质因子的次方大小，即 i 次（p^i^） 
			res = mul(res, primers[i]);
			
	for(int i = res.size() - 1; i >= 0; i--)
	printf("%d", res[i]);
	puts("");
	
	return 0;
 }

卡特兰问题

思想

这位博主写的非常好
蒟蒻豆进阶之路

取模
acwing算法基础课-第四章 数学知识_第9张图片
卡特兰数 —— 模板题 AcWing 889. 满足条件的01序列
给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为： Cat(n) = C(2n, n) / (n + 1)

AcWing 889 满足条件的01序列（模板题）

#include
using namespace std;
const int eps = 1e9 + 7;

int qmi(int a, int k ,int p)
{
	int res = 1;
	while(k)
	{
		if(k&1) res = (long long)res * a % p;
		a = (long long)a * a % p;
		k >>= 1;
	}
	return res;
}
int main()
{
	int n;
	cin >> n;
	int a = 2 * n;
	int b = n;
	int res = 1;
	// 2n(2n-1)(2n-2)……（2n-n+1） 
	for(int i = a; i > a - b; i--) res = (long long)res * i % eps;
	// qmi(1)*qmi(2)*qmi(3)……qmi(n) 
	for(int j = 1; j <= b; j++) res = (long long)res * qmi(j, eps - 2, eps) % eps;
	// qmi(n+1)
	res = (long long) res * qmi(n + 1, eps -2, eps) % eps;

	cout << res <<endl;
	return 0;
 }

容斥原理

思想

简介：在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。
定义：如果被计数的事物有A、B、C三类，那么，A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。（A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C） [2] 。
例如：一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？
分析：依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A类元素”，“语文得满分”称为“B类元素”，“语、数都是满分”称为“既是A类又是B类的元素”，“至少有一门得满分的同学”称为“A类和B类元素个数”的总和。为15+12-4=23。

公式：acwing算法基础课-第四章 数学知识_第10张图片
来自百度百科
公式证明：j_d_m_y

AcWing 890 能被整除的数

这位博主写的非常好，大家可以看看
Cloudeeeee
这里提一下重点
① 求出每个集合中元素的个数（ |Si| = n/pi）
② 求出集合和集合之间交集的个数（ |S1∩S2∩……Si| = n/(pip2……pi)）
③ 用二进制表示选择了哪个集合与否

对于③ ，我们知道p[i]的所有组合方式有 2m - 1 种
acwing算法基础课-第四章 数学知识_第11张图片
结合Cloudeeeee博主写的
acwing算法基础课-第四章 数学知识_第12张图片
我们可以从 1 ~ (m - 1)来遍历每种情况

代码实现思路：
1、每一个i代表一种可能的取法，最外层的循环遍历置2的m次方后，可以取完所有的取法
2、里面的循环就是提取出这个i值对应的取法
3、再将提取出的取法代入公式
转载自Cloudeeeee

#include
using namespace std;
const int N = 20;
int p[N]; //存储质数 

int main()
{
	int n, m;
	int res;
	cin >> n >> m;
	for(int i = 0; i < m; i++) cin >> p[i];
	//从 0 遍历到 2的 m 次方减一 ，这样每个情况都会遍历到 
	for(int i = 1; i < (1 << m); i++)
	{
		int s = 1, t = 0; //s表示质数相乘，t用于表示有几个质数 
		// 遍历每个质数，用于取出符合条件的质因子相乘 
		for(int j = 0; j < m; j++)
		{
		//用于选出二进制表示为 1的位数，其对应 p[j] 
			if(i >> j & 1)
			{   //质数相乘超出了范围 
				if((long long)p[j] * s > n)
				{
					s = -1;
					break;
				}
				s *= p[j]; //加入s（质数相乘的行列中） 
				t++;
			}
		}
		if(s != -1)
		{
			//奇数为 +， 偶数为 -  
			if(t % 2) res += n / s;
			else res -= n / s;
		}
	}
	printf("%d\n", res);
	return 0;
 }

博弈论

思想

NIM游戏 —— 模板题 AcWing 891. Nim游戏
给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。
NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

定理： NIM博弈先手必胜，当且仅当 A1 ^ A2 ^ … ^ An != 0

公平组合游戏ICG
若一个游戏满足：
由两名玩家交替行动；
在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
不能行动的玩家判负；
则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件2和条件3。

有向图游戏
给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

Mex运算
设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：
mex(S) = min{x}, x属于自然数，且x不属于S

SG函数
在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1, y2, …, yk，定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果，即：
SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

有向图游戏的和 —— 模板题 AcWing 893. 集合-Nim游戏
设G1, G2, …, Gm 是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏Gi，并在Gi上行动一步。G被称为有向图游戏G1, G2, …, Gm的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：
SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)

定理
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

作者：yxc
链接：https://www.acwing.com/blog/content/406/
来源：AcWing

必胜状态和必败状态
必胜状态：先手进行某一个操作，留给后手是一个必败状态时，对于先手来说是一个必胜状态。即先手可以走到某一个必败状态。
必败状态：先手无论如何操作，留给后手都是一个必胜状态时，对于先手来说是一个必败状态。即先手走不到任何一个必败状态。
结论
假设n堆石子，石子数目分别是a1,a2,…,an，如果a1⊕a2⊕…⊕an≠0，先手必胜；否则先手必
败。
————————————————
Cloudeeeee

问: 为什么公平组合游戏存在必胜与必败状态?

公平组合游戏指的是两个玩家交替进行操作的一种游戏，每个操作都从一组可行操作中选择一个，并改变游戏的状态。游戏在达到某个终止状态时结束，最终得分或胜负由终止状态决定。

对于公平组合游戏而言，存在必胜和必败状态的原因是基于一种数学原理，即游戏的状态可以通过其后继状态来进行分析。

假设我们将每个游戏状态视为节点，两个玩家的操作视为从一个状态到另一个状态的边。我们可以构建一个有向图，其中节点表示游戏状态，边表示操作。在这个有向图中，从初始状态开始，我们可以通过操作沿着边移动到其他状态。

现在考虑两种可能情况：

  1. 如果在当前状态下，存在一条边可以移动到一个必败状态，那么当前状态就是必胜状态。因为当前玩家可以选择这样的一条边，将游戏状态转移到必败状态，迫使对手处于必败状态。

  2. 如果在当前状态下，所有可能的边都导致必胜状态，或者不存在任何边可以移动到其他状态，那么当前状态就是必败状态。因为不管当前玩家选择哪条边，对手都可以在下一步移动后处于必胜状态，从而保证对手取胜。

基于上述原理，通过从终止状态向初始状态反向分析，我们可以确定哪些状态是必胜状态，哪些状态是必败状态。这种分析方法被称为"逆向归纳法"或"反向博弈论"。通过这种方法，我们可以确定公平组合游戏中的必胜和必败状态。
需要注意的是，这个结论仅适用于满足特定条件的公平组合游戏。在其他类型的游戏中，可能不存在必胜或必败状态，或者可能存在其他复杂的情况。

问：为什么公平组合游戏一般用异或就能判断必胜还是必败？

在某些特定的公平组合游戏中，可以使用异或（XOR）操作来判断一个状态是否是必胜状态。

这是因为在这些游戏中，每个状态都可以被表示为一组独立的子游戏的状态，并且这些子游戏是相互独立且可解决的。通过计算每个子游戏的状态，然后对这些状态进行异或操作，可以得到当前状态的异或和。根据这个异或和的结果，我们可以判断当前状态是必胜还是必败。

具体来说，假设我们将当前状态表示为一个整数，每个子游戏的状态也表示为相应的整数。我们可以计算当前状态的异或和，即将所有子游戏状态的整数进行异或操作。如果异或和为0，表示当前状态是必败状态；如果异或和不为0，表示当前状态是必胜状态。

这种判断方法的原理是基于以下观察：

  • 如果当前状态是必败状态，那么对于每个子游戏状态，它们的异或和为0，因为无论玩家选择哪个子游戏，对手总是可以找到一个合法的操作来使得异或和保持为0。
  • 如果当前状态是必胜状态，那么对于至少一个子游戏状态，它们的异或和不为0，因为当前玩家可以选择这个子游戏，并找到一个操作使得异或和不为0，从而保证取胜。

需要注意的是，这个判断方法仅适用于满足特定条件的公平组合游戏，并且需要将游戏状态和子游戏的状态映射到整数上。在其他类型的游戏中，可能不存在这种简单的判断方法，或者需要其他的分析技巧来确定必胜和必败状态。

yxc老师这么说：异或操作是判断必胜或必败的一种方式，至于为什么异或可以，大家可以参考 K-nim游戏 应该就明白了

AcWing 891 Nim 游戏（Nim游戏 - 模板题）

对于为什么
a1^ a2 ^ … ^an=0 先手必败
a1 ^ a2 ^ … ^an≠0 先手必胜
可以参考这位博主，将此问题讲的很好
糖豆爸爸

#include
using namespace std;

int main()
{
	int n;
	int res = 0;
	cin >> n;
	while(n--)
	{
		int x; 
		cin >> x;
		 res ^= x;
	}
	if(res) puts("Yes"); // 异或值非0， 必胜 
	else puts("No"); //  异或值为 0，必败 
	return 0;
 }

AcWing 892 台阶-Nim游戏

奇数级台阶上的石子异或和不为0，则先手胜；
奇数级台阶上的石子异或和为0，则先手败。

像上一题，拿掉石子，相当于把某一个奇数级台阶上的任意石子放到下面的偶数级台阶去。
还有一种情况，如果对手把上面偶数级台阶上的石子放到下面的奇数级台阶去，ok，我们镜像它，把它放到下面的偶数级台阶去，如果为地板，岂不完美。

这样，我们只需关注奇数级台阶上的石子异或和就可以。

#include
using namespace std;

int main()
{
	int n;
	int res = 0;
	int k = 1;
	cin >> n;
	while(n--)
	{
		int x;
		cin >> x;
		if(k % 2) 
		{
			res ^= x;
			k++;
		}
	}
	if(res == 0) puts("No");
	else puts("Yes"); 
	return 0;
}

AcWing 893 集合-Nim游戏（有向图游戏的和 - 模板题）

有向图游戏
给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
Mex运算
设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：
mex(S) = min{x}, x属于自然数，且x不属于S
SG函数
在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1, y2, …, yk，定义SG(x)为x的后继节点y1, y2, …, yk 的SG函数值构成的集合再执行mex(S)运算的结果，即：
SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。
有向图游戏的和 —— 模板题 AcWing 893. 集合-Nim游戏
设G1, G2, …, Gm 是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏Gi，并在Gi上行动一步。G被称为有向图游戏G1, G2, …, Gm的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：
SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)

定理
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

对于SG函数,是用于构成下面这张图的步骤，大家可以模拟一下。
注意 unordered_set s;表示当前的哈希表，返回时返回值进入另外一个哈希表，用来保证 mex()函数的完成 ，即下图中红色数字。

//用来求出每堆石子的SG值
int SG(int x)
{
	if(f[x] != -1) return f[x]; //记忆化搜索,用来保证每种状态只会被算一次
// 哈希表存储SG函数值
//注意这里是局部变量，返回时返回值进入另外一个哈希表，用来保证 mex()函数的完成 
	unordered_set<int> s;
	//遍历结点 x的下一条有向边 
	 for(int i = 0; i < m; i++)
	 {
	 	int sum = p[i];
	 	if(x >= sum) s.insert(SG(x - sum));
	 }
	 // Mex运算,返回不属于集合S的最小非负整数 
	 for(int j = 0; ; j++)
	 	if(!s.count(j)) return f[x] = j;
}

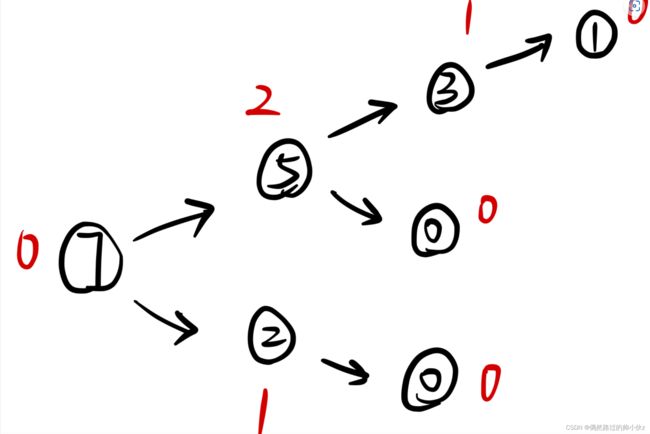
集合S中有k个数，表示每次只能取这k个数中的某一个数的石头。
如 k = 2,S = {2,5} ，表示S中有两个数，取石头时每次要么取2，要么取5。
n堆石子，如 n = 3,每堆分别有 2 4 7个石子。将每堆石子的取法看成一张有向图，此处取7，则取法的有向图如下：
acwing算法基础课-第四章 数学知识_第13张图片
所以 SG(G7) = 0 （初始状态的SG值），同理求出第一堆和第二堆的SG值，SG(G2) ，SG(G4)
然后把每堆石子的SG值异或起来，
则最终结果SG = SG(G2) ⊕ SG(G4) ⊕ SG(G7)
来源于Cloudeeeee

#include
#include
#include
using namespace std;
const int N = 110;
const int M = 10010;
int n, m;
int p[N]; //数字集合 S 
int f[M]; 

//用来求出每堆石子的SG值
int SG(int x)
{
	if(f[x] != -1) return f[x]; //记忆化搜索,用来保证每种状态只会被算一次
// 哈希表存储SG函数值
//注意这里是局部变量，返回时返回值进入另外一个哈希表，用来保证 mex()函数的完成 
	unordered_set<int> s;
	//遍历结点 x的下一条有向边 
	 for(int i = 0; i < m; i++)
	 {
	 	int sum = p[i];
	 	if(x >= sum) s.insert(SG(x - sum));
	 }
	 // Mex运算,返回不属于集合S的最小非负整数 
	 for(int j = 0; ; j++)
	 	if(!s.count(j)) return f[x] = j;
}

int main()
{
	int res = 0;
	cin >> m;
	for(int i = 0; i < m; i++) cin >> p[i];
	
	cin >>n;
	memset(f, -1, sizeof f);
	
	while(n--)
	{
		int x;
		cin >> x;
		res ^= SG(x);//异或每堆石子的SG值 
	}
	
	if(res) puts("Yes");
	else puts("No");
	
	return 0;
 }

AcWing 894 拆分-Nim游戏

acwing算法基础课-第四章 数学知识_第14张图片
对于这题，对于这题，题目我一开始理解错了。
不是某堆的新的两堆可以加到另一原有的堆，而是有新的两堆代替这一堆，但新的两堆石子数都不大于这一堆的石子数

比如有三堆，（2 3 6 ），取为 6 的堆，可以拆为
0 0
0 1
0 2
0 3
0 4
0 5
…
1 0
1 2
1 3
1 4
1 5
…
5 0
5 1
5 2
5 3
5 4
5 5
但是其拆开的两堆不会加到原来的第一堆(2)，第二堆(3)中

重要思路
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：
SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)
对于每个SG(Gi)，考虑所有的局面，用mex运算计算出sg值
acwing算法基础课-第四章 数学知识_第15张图片

#include
#include
#include
using namespace std;
const int N = 110;
int f[N];

int sg(int x)
{
	if(f[x] != -1) return f[x];
	unordered_set<int> s;
	//所有的局面 
	for(int i = 0; i < x; i++)
	for(int j = 0; j <= i; j++)
	s.insert(sg(i) ^ sg(j));
	
	for(int i = 0; ; i++)
	if(!s.count(i)) return f[x] = i;
}

int main()
{
	memset(f, -1, sizeof f);
	int n;
	cin >> n;
	int res = 0;
	while(n--)
	{
		int x;
		cin >> x;
		res ^= sg(x);
	}
	if(res) puts("Yes");
	else puts("No");
	
	
	return 0;
 }

你可能感兴趣的:(#,算法,-,acwing算法基础课,算法,c++)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • c++ 的iostream 和 c++的stdio的区别和联系 黄卷青灯77 c++算法开发语言iostreamstdio
    在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • 基于社交网络算法优化的二维最大熵图像分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法php开发语言
    智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
  • 121. 买卖股票的最佳时机 薄荷糖的味道_fb40
    给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
  • 【JS】执行时长(100分) |思路参考+代码解析（C++） l939035548 JS算法数据结构c++
    题目为了充分发挥GPU算力，需要尽可能多的将任务交给GPU执行，现在有一个任务数组，数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务，一次执行耗时1秒，在保证GPU不空闲情况下，最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数，取值范围[1,10000]第二个参数为任务数组长度，取值范围[1,10000]第三个参数为任务数组，数字范围
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • 基于CODESYS的多轴运动控制程序框架：逻辑与运动控制分离，快速开发灵活操作 GPJnCrbBdl python开发语言
    基于codesys开发的多轴运动控制程序框架，将逻辑与运动控制分离，将单轴控制封装成功能块，对该功能块的操作包含了所有的单轴控制（归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等）。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式，程序状态的跳转都已完成，只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义，能帮助开发者快速
  • C++ | Leetcode C++题解之第409题最长回文串 Ddddddd_158 经验分享C++Leetcode题解
    题目：题解：classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
  • C++菜鸟教程 - 从入门到精通 第二节 DreamByte c++
    一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
    前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
  • k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
    ?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
  • Python实现简单的机器学习算法 master_chenchengg pythonpython办公效率python开发IT
    Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
  • 推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
    importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
  • K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习K近邻
    importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
  • Java面试题精选：消息队列(二) 芒果不是芒 Java面试题精选javakafka
    一、Kafka的特性1.消息持久化：消息存储在磁盘，所以消息不会丢失2.高吞吐量：可以轻松实现单机百万级别的并发3.扩展性：扩展性强，还是动态扩展4.多客户端支持：支持多种语言（Java、C、C++、GO、）5.KafkaStreams（一个天生的流处理）:在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制：Kafka进行生产或者消费的时候会
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
    今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
  • Python算法L5：贪心算法 小熊同学哦 Python算法算法python贪心算法
    Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
  • C++ lambda闭包消除类成员变量 barbyQAQ c++c++java算法
    原文链接：https://blog.csdn.net/qq_51470638/article/details/142151502一、背景在面向对象编程时，常常要添加类成员变量。然而类成员一旦多了之后，也会带来干扰。拿到一个类，一看成员变量好几十个，就问你怕不怕？二、解决思路可以借助函数式编程思想，来消除一些不必要的类成员变量。三、实例举个例子：classClassA{public:...intfu
  • 2021 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级C++语言试题 （第三大题：完善程序 代码） mmz1207 c++csp
    最近有一段时间没更新了，在准备CSP考试，请大家见谅。（1）有n个人围成一个圈，依次标号0到n-1。从0号开始，依次0，1，0，1...交替报数，报到一的人离开，直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
  • 《 C++ 修炼全景指南：九 》打破编程瓶颈！掌握二叉搜索树的高效实现与技巧 Lenyiin C++修炼全景指南技术指南c++算法stl
    摘要本文详细探讨了二叉搜索树（BinarySearchTree,BST）的核心概念和技术细节，包括插入、查找、删除、遍历等基本操作，并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度，同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类，读者能够掌握其实际应用，此外，文章还建议进一步扩展为平衡树（如AVL树、红黑树）以优化极端情况下的性能退化。
  • 20个新手学习c++必会的程序 输出*三角形、杨辉三角等（附代码） X_StarX c++学习算法大学生开发语言数据结构
    示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
  • C++八股 Petrichorzncu 八股总结c++开发语言
    这里写目录标题C++内存管理C++的构造函数，复制构造函数，和析构函数深复制与浅复制：构造函数和析构函数哪个能写成虚函数，为什么？C++数据结构内存排列结构体和类占用的内存：==虚函数和虚表的原理==虚函数虚表（Vtable）虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
  • 【2022 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级 C++语言试题及解析】 汉子萌萌哒 CCFnoi算法数据结构c++
    一、单项选择题(共15题，每题2分，共计30分；每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持：()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识，面向对象和类有关，类又涉及父类、子类、继承、派生等关系，printf
  • 《 C++ 修炼全景指南：十 》自平衡的艺术：深入了解 AVL 树的核心原理与实现 Lenyiin C++修炼全景指南技术指南c++数据结构stl
    摘要本文深入探讨了AVL树（自平衡二叉搜索树）的概念、特点以及实现细节。我们首先介绍了AVL树的基本原理，并详细分析了其四种旋转操作，包括左旋、右旋、左右双旋和右左双旋，阐述了它们在保持树平衡中的重要作用。接着，本文从头到尾详细描述了AVL树的插入、删除和查找操作，配合完整的代码实现和详尽的注释，使读者能够全面理解这些操作的执行过程。此外，我们还提供了AVL树的遍历方法，包括中序、前序和后序遍历，
  • 【RabbitMQ 项目】服务端：数据管理模块之绑定管理 月夜星辉雪 rabbitmq分布式
    文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
  • JAVA学习笔记之23种设计模式学习 victorfreedom Java技术设计模式androidjava常用设计模式
    博主最近买了《设计模式》这本书来学习，无奈这本书是以C++语言为基础进行说明，整个学习流程下来效率不是很高，虽然有的设计模式通俗易懂，但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番，发现有大神写过了这方面的问题，于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类：创建型模式，共五种：工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式，共七种：适配器
  • ztree异步加载 3213213333332132 JavaScriptAjaxjsonWebztree
    相信新手用ztree的时候,对异步加载会有些困惑，我开始的时候也是看了API花了些时间才搞定了异步加载，在这里分享给大家。 我后台代码生成的是json格式的数据，数据大家按各自的需求生成，这里只给出前端的代码。 设置setting，这里只关注async属性的配置 var setting = { //异步加载配置
  • thirft rpc 具体调用流程 BlueSkator 中间件rpcthrift
    Thrift调用过程中，Thrift客户端和服务器之间主要用到传输层类、协议层类和处理类三个主要的核心类，这三个类的相互协作共同完成rpc的整个调用过程。在调用过程中将按照以下顺序进行协同工作：         （1）     将客户端程序调用的函数名和参数传递给协议层（TProtocol），协议
  • 异或运算推导, 交换数据 dcj3sjt126com PHP异或^
    /* * 5 0101 * 9 1010 * * 5 ^ 5 * 0101 * 0101 * ----- * 0000 * 得出第一个规律: 相同的数进行异或, 结果是0 * * 9 ^ 5 ^ 6 * 1010 * 0101 * ---- * 1111 * * 1111 * 0110 * ---- * 1001
  • 事件源对象 周华华 JavaScript
    <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml&q
  • MySql配置及相关命令 g21121 mysql
            MySQL安装完毕后我们需要对它进行一些设置及性能优化，主要包括字符集设置，启动设置，连接优化，表优化，分区优化等等。           一 修改MySQL密码及用户      
  • [简单]poi删除excel 2007超链接 53873039oycg Excel
          采用解析sheet.xml方式删除超链接，缺点是要打开文件2次,代码如下:      public void removeExcel2007AllHyperLink(String filePath) throws Exception { OPCPackage ocPkg = OPCPac
  • Struts2添加 open flash chart 云端月影
    准备以下开源项目： 1. Struts 2.1.6 2. Open Flash Chart 2 Version 2 Lug Wyrm Charmer (28th, July 2009) 3. jofc2，这东西不知道是没做好还是什么意思，好像和ofc2不怎么匹配，最好下源码，有什么问题直接改。 4. log4j 用eclipse新建动态网站，取名OFC2Demo，将Struts2 l
  • spring包详解 aijuans spring
    下载的spring包中文件及各种包众多，在项目中往往只有部分是我们必须的，如果不清楚什么时候需要什么包的话，看看下面就知道了。 aspectj目录下是在Spring框架下使用aspectj的源代码和测试程序文件。Aspectj是java最早的提供AOP的应用框架。 dist 目录下是Spring 的发布包，关于发布包下面会详细进行说明。 docs&nb
  • 网站推广之seo概念 antonyup_2006 算法Web应用服务器搜索引擎Google
       持续开发一年多的b2c网站终于在08年10月23日上线了。作为开发人员的我在修改bug的同时，准备了解下网站的推广分析策略。     所谓网站推广，目的在于让尽可能多的潜在用户了解并访问网站，通过网站获得有关产品和服务等信息，为最终形成购买决策提供支持。     网站推广策略有很多，seo，email，adv
  • 单例模式,sql注入,序列 百合不是茶 单例模式序列sql注入预编译
      序列在前面写过有关的博客,也有过总结,但是今天在做一个JDBC操作数据库的相关内容时 需要使用序列创建一个自增长的字段  居然不会了,所以将序列写在本篇的前面    1,序列是一个保存数据连续的增长的一种方式; 序列的创建; CREATE SEQUENCE seq_pro 2 INCREMENT BY 1 -- 每次加几个 3
  • Mockito单元测试实例 bijian1013 单元测试mockito
    Mockito单元测试实例： public class SettingServiceTest { private List<PersonDTO> personList = new ArrayList<PersonDTO>(); @InjectMocks private SettingPojoService settin
  • 精通Oracle10编程SQL(9)使用游标 bijian1013 oracle数据库plsql
    /* *使用游标 */ --显示游标 --在显式游标中使用FETCH...INTO语句 DECLARE CURSOR emp_cursor is select ename,sal from emp where deptno=1; v_ename emp.ename%TYPE; v_sal emp.sal%TYPE; begin ope
  • 【Java语言】动态代理 bit1129 java语言
      JDK接口动态代理 JDK自带的动态代理通过动态的根据接口生成字节码(实现接口的一个具体类)的方式，为接口的实现类提供代理。被代理的对象和代理对象通过InvocationHandler建立关联   package com.tom; import com.tom.model.User; import com.tom.service.IUserService;
  • Java通信之URL通信基础 白糖_ javajdkwebservice网络协议ITeye
    java对网络通信以及提供了比较全面的jdk支持，java.net包能让程序员直接在程序中实现网络通信。 在技术日新月异的现在，我们能通过很多方式实现数据通信，比如webservice、url通信、socket通信等等，今天简单介绍下URL通信。 学习准备：建议首先学习java的IO基础知识   URL是统一资源定位器的简写，URL可以访问Internet和www，可以通过url
  • 博弈Java讲义 - Java线程同步 (1) boyitech java多线程同步锁
      在并发编程中经常会碰到多个执行线程共享资源的问题。例如多个线程同时读写文件，共用数据库连接，全局的计数器等。如果不处理好多线程之间的同步问题很容易引起状态不一致或者其他的错误。    同步不仅可以阻止一个线程看到对象处于不一致的状态，它还可以保证进入同步方法或者块的每个线程，都看到由同一锁保护的之前所有的修改结果。处理同步的关键就是要正确的识别临界条件（cri
  • java-给定字符串，删除开始和结尾处的空格，并将中间的多个连续的空格合并成一个。 bylijinnan java
    public class DeleteExtraSpace { /** * 题目：给定字符串，删除开始和结尾处的空格，并将中间的多个连续的空格合并成一个。 * 方法1.用已有的String类的trim和replaceAll方法 * 方法2.全部用正则表达式，这个我不熟 * 方法3.“重新发明轮子”，从头遍历一次 */ public static v
  • An error has occurred.See the log file错误解决！ Kai_Ge MyEclipse
    今天早上打开MyEclipse时，自动关闭！弹出An error has occurred.See the log file错误提示！ 很郁闷昨天启动和关闭还好着！！！打开几次依然报此错误，确定不是眼花了！ 打开日志文件！找到当日错误文件内容： --------------------------------------------------------------------------
  • [矿业与工业]修建一个空间矿床开采站要多少钱? comsci
           地球上的钛金属矿藏已经接近枯竭...........        我们在冥王星的一颗卫星上面发现一些具有开采价值的矿床.....        那么,现在要编制一个预算,提交给财政部门..
  • 解析Google Map Routes dai_lm google api
    为了获得从A点到B点的路劲，经常会使用Google提供的API，例如 [url] http://maps.googleapis.com/maps/api/directions/json?origin=40.7144,-74.0060&destination=47.6063,-122.3204&sensor=false [/url] 从返回的结果上，大致可以了解应该怎么走，但
  • SQL还有多少“理所应当”？ datamachine sql
    转贴存档，原帖地址：http://blog.chinaunix.net/uid-29242841-id-3968998.html、http://blog.chinaunix.net/uid-29242841-id-3971046.html！ ------------------------------------华丽的分割线--------------------------------
  • Yii使用Ajax验证时，如何设置某些字段不需要验证 dcj3sjt126com Ajaxyii
    经常像你注册页面,你可能非常希望只需要Ajax去验证用户名和Email,而不需要使用Ajax再去验证密码,默认如果你使用Yii 内置的ajax验证Form,例如: $form=$this->beginWidget('CActiveForm', array(        'id'=>'usuario-form',&
  • 使用git同步网站代码 dcj3sjt126com crontabgit
    转自:http://ued.ctrip.com/blog/?p=3646?tn=gongxinjun.com   管理一网站，最开始使用的虚拟空间，采用提供商支持的ftp上传网站文件，后换用vps，vps可以自己搭建ftp的，但是懒得搞，直接使用scp传输文件到服务器，现在需要更新文件到服务器，使用scp真的很烦。发现本人就职的公司，采用的git+rsync的方式来管理、同步代码，遂
  • sql基本操作 蕃薯耀 sqlsql基本操作sql常用操作
    sql基本操作 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年6月1日 17:30:33 星期一     &
  • Spring4+Hibernate4+Atomikos3.3多数据源事务管理 hanqunfeng Hibernate4
    Spring3+后不再对JTOM提供支持，所以可以改用Atomikos管理多数据源事务。Spring2.5+Hibernate3+JTOM参考：http://hanqunfeng.iteye.com/blog/1554251Atomikos官网网站：http://www.atomikos.com/   一.pom.xml <dependency> <
  • jquery中两个值得注意的方法one()和trigger()方法 jackyrong trigger
      在jquery中，有两个值得注意但容易忽视的方法，分别是one()方法和trigger()方法,这是从国内作者<<jquery权威指南》一书中看到不错的介绍 1） one方法     one方法的功能是让所选定的元素绑定一个仅触发一次的处理函数，格式为    one(type,${data},fn) &nb
  • 拿工资不仅仅是让你写代码的 lampcy 工作面试咨询
    这是我对团队每个新进员工说的第一件事情。这句话的意思是，我并不关心你是如何快速完成任务的，哪怕代码很差，只要它像救生艇通气门一样管用就行。这句话也是我最喜欢的座右铭之一。 这个说法其实很合理：我们的工作是思考客户提出的问题，然后制定解决方案。思考第一，代码第二，公司请我们的最终目的不是写代码，而是想出解决方案。 话粗理不粗。 付你薪水不是让你来思考的，也不是让你来写代码的，你的目的是交付产品
  • 架构师之对象操作----------对象的效率复制和判断是否全为空 nannan408 架构师
    1.前言。   如题。 2.代码。 (1)对象的复制，比spring的beanCopier在大并发下效率要高，利用net.sf.cglib.beans.BeanCopier Src src=new Src(); BeanCopier beanCopier = BeanCopier.create(Src.class, Des.class, false);
  • ajax 被缓存的解决方案 Rainbow702 JavaScriptjqueryAjaxcache缓存
    使用jquery的ajax来发送请求进行局部刷新画面，各位可能都做过。 今天碰到一个奇怪的现象，就是，同一个ajax请求，在chrome中，不论发送多少次，都可以发送至服务器端，而不会被缓存。但是，换成在IE下的时候，发现，同一个ajax请求，会发生被缓存的情况，只有第一次才会被发送至服务器端，之后的不会再被发送。郁闷。 解决方法如下： ① 直接使用 JQuery提供的 “cache”参数，
  • 修改date.toLocaleString()的警告 tntxia String
      我们在写程序的时候，经常要查看时间，所以我们经常会用到date.toLocaleString()，但是date.toLocaleString()是一个过时 的API，代替的方法如下：   package com.tntxia.htmlmaker.util; import java.text.SimpleDateFormat; import java.util.
  • 项目完成后的小总结 xiaomiya js总结项目
    项目完成了，突然想做个总结但是有点无从下手了。 做之前对于客户端给的接口很模式。然而定义好了格式要求就如此的愉快了。 先说说项目主要实现的功能吧 1，按键精灵 2，获取行情数据 3，各种input输入条件判断 4，发送数据（有json格式和string格式） 5，获取预警条件列表和预警结果列表， 6，排序， 7，预警结果分页获取 8，导出文件（excel，text等） 9，修
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他