代码随想录第四十八天 | 动态规划 打家劫舍问题：数组上的动规：基本型（198），环形（213）；树形动规：暴力递归，记忆化递推，树形动规（337）；C++ map 查找 key 是否存在

1、打家劫舍问题：数组上的动规

1.1 leetcode 198：打家劫舍

第一遍代码
对于递归式，对应节点的最大值有两种来源：对应节点是偷 还是不偷，最后是取最大值

dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);

注意 i比对应位置nums下标多1
dp数组表示 到第下标节点能偷到的最高金额

class Solution {
public:
    int rob(vector<int>& nums) {
        //对应节点的最大值有两种来源：对应节点是偷还是不偷，取最大值
        vector<int> dp(nums.size() + 1, 0);//到第下标节点能偷到的最高金额
        dp[1] = nums[0];
        for(int i = 2; i <= nums.size(); i++) {
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);
            //注意i比对应位置nums下标多1
        }
        return dp[nums.size()];
    }
};

代码随想录思路
与第一遍代码思路基本一致，不同点在于第一遍代码参考了之前0-1背包的思路，给dp数组多开了一个，而代码随想录思路就开了nums.size() 个dp数组，导致初始化有点不一样

当前的状态我是偷还是不偷呢？
当前房屋偷与不偷 取决于 前一个房屋和前两个房屋是否被偷了
所以这里就更感觉到，当前状态和前面状态会有一种依赖关系，那么这种依赖关系都是动规的递推公式

动规五部曲分析如下：
1、确定dp数组（dp table）以及下标的含义
dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]

2、确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出 下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额 为 dp[i-2] 加上第i房间偷到的钱
如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

3、dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出，递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲，dp[0] 一定是 nums[0]，dp[1]就是 nums[0] 和 nums[1] 的最大值即：dp[1] = max(nums[0], nums[1]);
代码如下：

vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);

4、确定遍历顺序
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历（后面还有树形遍历）
代码如下：

for (int i = 2; i < nums.size(); i++) {
    dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}

5、举例推导dp数组
以示例二，输入[2,7,9,3,1]为例

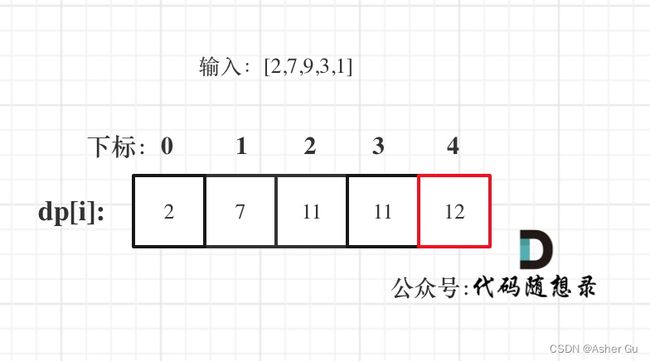
红框dp[nums.size() - 1]为结果
C++代码如下：

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for (int i = 2; i < nums.size(); i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.size() - 1];
    }
};

时间复杂度: O(n)
空间复杂度: O(n)

打家劫舍是DP解决的经典题目，这道题也是打家劫舍入门级题目，后面我们还会变种方式来打劫的

1.2 leetcode 213：环形 打家劫舍

这里变成了一个环，由于涉及到最后一个元素时第一个元素已经早就确定过了，但是当比较到最后一个元素的时候并没办法知道第一个元素是不是被用了，如果不使用第一个元素使用最后一个元素的情况下会不会让结果更好呢？如果用环取余来做，对最后一个元素来说，除了考虑之前的元素还要考虑之后的元素，循环就不知道方向了

代码随想录思路
这道题目和 leetcode 198：打家劫舍 是差不多的，唯一区别就是成环了

对于一个数组，成环的话主要有如下三种情况：
情况一：考虑不包含首尾元素

情况二：考虑包含首元素，不包含尾元素

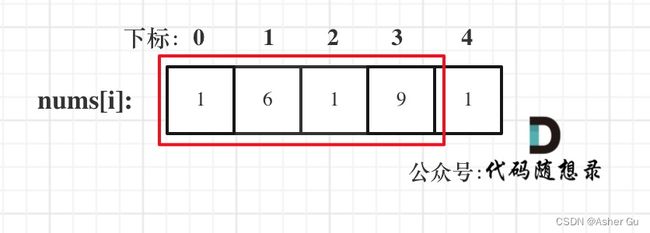
情况三：考虑包含尾元素，不包含首元素

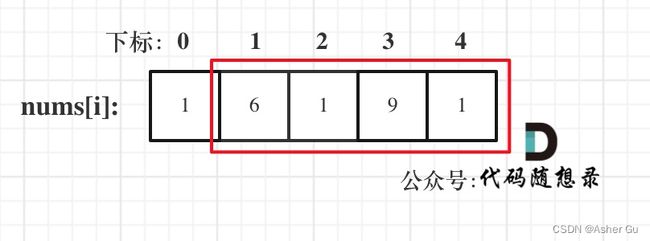
注意我这里用的是 “考虑”，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！ 对于情况三，取nums[1] 和 nums[3]就是最大的
而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了
总之就是 避免最后一个元素和第一个元素同时取到，在这里直接变成 避免最后一个元素和第一个元素同时考虑到

分析到这里，本题其实比较简单了。 剩下的和 leetcode 198：打家劫舍 就是一样的了

根据思路实现代码：
对于getMax函数：左闭右闭 leetcode 198：打家劫舍 相同思路
还要再考虑只有一个数的情况，比如输入是[1]，如果按下面的return逻辑就两个数组都考虑不到1

 return max(getMax(nums, 0, nums.size() - 2), getMax(nums, 1, nums.size() - 1));

class Solution {
public:
    int getMax(vector<int>& nums, int startIndex, int endIndex) {
        //左闭右闭 leetcode 198：打家劫舍 相同思路
        if(startIndex > endIndex) return 0;
        vector<int> dp(endIndex - startIndex + 1, 0);
        dp[0] = nums[startIndex];
        if(endIndex - startIndex > 0) {
            dp[1] = max(nums[startIndex], nums[startIndex + 1]);
        }
        for(int i = startIndex + 2; i <= endIndex; i++) {
            dp[i - startIndex] = max(dp[i - startIndex - 1], dp[i - startIndex - 2] + nums[i]);
        }
        return dp[endIndex - startIndex];
    }
    int rob(vector<int>& nums) {
        //还要再考虑只有一个数的情况，比如输入是[1]，如果按下面的return逻辑就两个数组都考虑不到1
        if(nums.size() == 1) {
            return nums[0];
        }
        return max(getMax(nums, 0, nums.size() - 2), getMax(nums, 1, nums.size() - 1));
    }
};

代码随想录实现代码（与自己代码一致）：

// 注意注释中的情况二情况三，以及把198.打家劫舍的代码抽离出来了
class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        int result1 = robRange(nums, 0, nums.size() - 2); // 情况二
        int result2 = robRange(nums, 1, nums.size() - 1); // 情况三
        return max(result1, result2);
    }
    // 198.打家劫舍的逻辑
    int robRange(vector<int>& nums, int start, int end) {
        if (end == start) return nums[start];
        vector<int> dp(nums.size());
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }

时间复杂度: O(n)
空间复杂度: O(n)

1.3 leetcode 213：总结

本文重点强调了情况一二三是 “考虑”的范围，而具体房间偷与不偷交给递推公式去抉择
这样大家就不难理解情况二和情况三包含了情况一了

2、打家劫舍问题：树形动规

2.1 leetcode 337：树上的 打家劫舍

没有思路，怎么保证二叉树在纵向上一隔一，但其实想起来之前做过类似，在贪心里面，后序遍历，分情况讨论，leetcode 968：监控二叉树 对二叉树进行有控制的遍历

代码随想录思路：
对于树的话，首先就要想到遍历方式，前中后序（深度优先搜索）还是层序遍历（广度优先搜索）
本题一定是要后序遍历，因为通过递归函数的返回值来做下一步计算

与 leetcode 198：打家劫舍，leetcode 213：打家劫舍II 一样，关键是要讨论当前节点抢还是不抢
如果抢了当前节点，两个孩子就不能动，如果没抢当前节点，就可以考虑抢左右孩子（注意这里说的是 “考虑”）

2.2 leetcode 337：暴力递归

代码随想录代码：
注意返回条件，root为空的时候 以及 root的左右节点为空的时候，正好对应两种情况分别判断不下去的情况

class Solution {
public:
    int rob(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right == NULL) return root->val;
        // 偷父节点
        int val1 = root->val;
        if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left，相当于不考虑左孩子了
        if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right，相当于不考虑右孩子了
        // 不偷父节点
        int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
        return max(val1, val2);
    }
};

根据思路自己写代码：
注意注释

class Solution {
public:
    int rob(TreeNode* root) {
        if(root == nullptr) {
            return 0;
        }
        if(root->left == nullptr && root->right == nullptr) {
            return root->val;
        }
        int val;//该节点偷的时候的金额
        int leftVal = 0;
        int rightVal = 0;
        if(root->left) leftVal = rob(root->left->left) + rob(root->left->right);
        if(root->right) rightVal = rob(root->right->left) + rob(root->right->right);
        val = leftVal + rightVal + root->val;//别忘了加自己的值
        //与该节点不偷的时候作比较
        return max(val, rob(root->left) + rob(root->right));
    }
};

当然纯暴力超时了

这个递归的过程中其实是有重复计算
我们计算了root的四个孙子（左右孩子的孩子）为头结点的子树的情况，又计算了root的左右孩子为头结点的子树的情况，计算左右孩子的时候其实又把孙子计算了一遍（改进的方向，点名了需要 “记忆” 哪些东西，即需要记忆 已经整出来的节点的 最多金额）

 return max(val, rob(root->left) + rob(root->right));

计算左右孩子的时候再执行这行代码会把之前算过的 rob(root->left->left) 等等再算一遍

2.3 leetcode 337：记忆化递推

可以使用一个map把计算过的结果保存一下，这样如果计算过孙子了，那么计算孩子的时候可以复用孙子节点的结果

代码随想录代码如下：

class Solution {
public:
    unordered_map<TreeNode* , int> umap; // 记录计算过的结果
    int rob(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right == NULL) return root->val;
        if (umap[root]) return umap[root]; // 如果umap里已经有记录则直接返回
        // 偷父节点
        int val1 = root->val;
        if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left
        if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right
        // 不偷父节点
        int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
        umap[root] = max(val1, val2); // umap记录一下结果
        return max(val1, val2);
    }
};

时间复杂度：O(n)
空间复杂度：O(log n)，算上递推系统栈的空间

根据思路自己实现代码：

2.4 C++ map 查找 key 是否存在

（来自 C++map key不存在）
1、在map中，由key查找value时，首先要判断map中是否包含key
2、如果不检查，直接返回map[key]，可能会出现意想不到的行为。如果map包含key，没有问题，如果map不包含key，使用下标有一个危险的副作用，会在map中插入一个key的元素，value取默认值，返回value。也就是说，map[key]不可能返回null
3、map提供了两种方式，查看是否包含key，m.count(key)，m.find(key)
4、m.count(key)：由于map不包含重复的key，因此m.count(key)取值为0，或者1，表示是否包含
5、m.find(key)：返回迭代器，判断是否存在

对于下面的场景，存在key就使用，否则返回null，有下面两种写法：
1、m.count()

if(m.count(key) > 0)
{
    return m[key];
}
return null;

2、m.find()

iter = m.find(key);
if(iter!=m.end())
{
    return iter->second;
}
return null;

这里需要注意：前一种方法很直观，但是效率差很多。因为前面的方法，需要执行两次查找。因此，推荐使用后一种方法

class Solution {
public:
    unordered_map<TreeNode*, int> mymap;
    int rob(TreeNode* root) {
        if(root == nullptr) {
            return 0;
        }
        if(root->left == nullptr && root->right == nullptr) {
            return root->val;
        }
        if(mymap.find(root) != mymap.end()) return mymap[root];//一旦找到就直接返回
        int val;//该节点偷的时候的金额
        int leftVal = 0;
        int rightVal = 0;
        if(root->left) leftVal = rob(root->left->left) + rob(root->left->right);
        if(root->right) rightVal = rob(root->right->left) + rob(root->right->right);
        val = leftVal + rightVal + root->val;//别忘了加自己的值
        //与该节点不偷的时候作比较
        mymap[root] = max(val, rob(root->left) + rob(root->right));
        return mymap[root];
    }
};

2.5 leetcode 337：树形动规（循环顺序 为 在树上的递归遍历）

在上面两种方法，其实对一个节点 偷与不偷 得到的最大金钱都没有做记录，而是需要实时计算（记忆化递推减少了一部分重复的树节点得到的最大金钱的计算，但是并没有涉及到 对一个节点 偷与不偷 得到的最大金钱 的记录）
而动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为2的数组，记录当前节点 偷与不偷 所得到的的最大金钱

这道题目算是树形dp的入门题目，因为是在树上进行状态转移，我们在讲解二叉树的时候说过递归三部曲，那么下面我以递归三部曲为框架，其中融合动规五部曲的内容来进行讲解

在树上进行dp，需要融合递归返回信息，跟顺序遍历不一样，顺序遍历直接用数组保存，意味着可以跨几个层次，寻找之前 再之前的结果，所以不需要管之前的节点是不是取，只要记录到某个节点的金额最大值即可；而树因为遍历过程中最多跨一层（后序左右中 两层，跨了一层），所以既要记录偷的，也要记录不偷的

1、确定递归函数的参数和返回值，第一次出现 返回值 / dp数组中的单一元素 是数组
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱，那么返回值就是一个长度为2的数组

参数为当前节点，代码如下：

vector<int> robTree(TreeNode* cur) {

其实这里的返回数组就是dp数组
所以dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱
所以本题dp数组就是一个长度为2的数组

长度为2的数组 怎么标记树中每个节点的状态呢？
别忘了在递归的过程中，系统栈会保存 每一层递归的参数

2、确定终止条件
在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0，所以就返回

if (cur == NULL) return vector<int>{0, 0};

这也相当于dp数组的初始化

3、确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算
通过递归左节点，得到左节点偷与不偷的金钱
通过递归右节点，得到右节点偷与不偷的金钱

代码如下：

// 下标0：不偷，下标1：偷
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右
// 中

4、确定单层递归的逻辑
如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0];

如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的（不是说一定就偷了），所以：val2 = max(left[0], left[1]) + max(right[0], right[1]);

最后当前节点的状态就是{val2, val1}; 即：{不偷当前节点得到的最大金钱，偷当前节点得到的最大金钱}

代码如下：

vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右

// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};

5、举例推导dp数组
以示例1为例，dp数组状态如下：（注意用后序遍历的方式推导）

最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱

递归三部曲与动规五部曲分析完毕，C++代码如下：

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }
    // 长度为2的数组，0：不偷，1：偷
    vector<int> robTree(TreeNode* cur) {
        if (cur == NULL) return vector<int>{0, 0};
        vector<int> left = robTree(cur->left);
        vector<int> right = robTree(cur->right);
        // 偷cur，那么就不能偷左右节点。
        int val1 = cur->val + left[0] + right[0];
        // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};

时间复杂度：O(n)，每个节点只遍历了一次
空间复杂度：O(log n)，算上递推系统栈的空间

根据思路自己实现：

class Solution {
public:
    vector<int> getNode(TreeNode* cur) {
        if(cur == nullptr) return {0, 0};
        vector<int> left = getNode(cur->left);
        vector<int> right = getNode(cur->right);
        //先计算cur不偷的时候，返回的vector第一个值是该节点不偷的时候，第二个值是该节点偷的时候
        int val1 = max(left[0], left[1]) + max(right[0], right[1]);
        //计算cur偷的时候
        int val2 = cur->val + left[0] + right[0];
        return {val1, val2};
    }

    int rob(TreeNode* root) {
        vector<int> res = getNode(root);
        return max(res[0], res[1]);
    }
};

2.6 leetcode 337：总结

这道题是树形DP的入门题目，通过这道题目大家应该也了解了，所谓树形DP就是在树上进行递归公式的推导

只不过平时我们习惯了在一维数组或者二维数组上推导公式，一下子换成了树，就需要对树的遍历方式足够了解，因为树的遍历的特殊限制（只能跨一层），所以返回值 递推公式发生了改变