Noip2021模拟赛题解
Noip2021模拟测试赛(一)
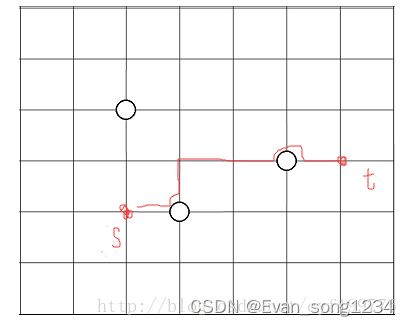
A 游戏
A A A 先从 ( 1 , 1 ) (1,1) (1,1) 移动到 ( 2 , m ) (2, m) (2,m), B B B 再从 ( 1 , 1 ) (1,1) (1,1) 移动到 ( 2 , m ) (2, m) (2,m)。
容易知道, A A A 移动一定是先右移任意格,再下移一格,最后右移到 ( 2 , m ) (2,m) (2,m)。
最终会剩下右上角,左下角两个区域没取。 B B B 只能取其中一个区域。
所以 O ( m ) O(m) O(m) 枚举,暴力计算答案。
B 公司补偿
简单 DP 非常容易,但由于 d d d 极大,所以会爆。
但是可以发现确定工资后,最多只有 n n n 种不同工资。
我们只考虑工资之间的大小关系,再用 DP 计算。
这时要使用组合数,但是可能有重,所以容斥。
C 无聊的线段
如果我们固定选择线段的权值的范围 [ l , r ] [l, r] [l,r],显然将权值在 [ l , r ] [l, r] [l,r] 之内的线段全部选择。
容易发现, l , r l, r l,r 一定是某一个线段的权值,因为不是线段的权值的 l , r l, r l,r 不优。
发现, l l l 增大时,为了满足要求 r r r 不会减小。
所以,双指针 O ( n ) O(n) O(n)。
问题来了,怎么判断是否满足要求?
我们用并查集线段覆盖的节点?还是其他?
线段树区修区查。
对于一个新增线段 [ l , r ] [l, r] [l,r] 我们让 [ l , r − 1 ] [l, r -1] [l,r−1] 的点值全部加 1 1 1。减去则相反。
查询则查询 [ 1 , m − 1 ] [1, m-1] [1,m−1] 的最小值是否为 0 0 0。
Noip2021模拟测试赛(二)
B 点对游戏
可以发现,每个人取的节点数量是固定的,所以我们考虑单独计算,假设为 x x x。
由于完全随机,所以每个节点被选取的概率也是一样的,为 C n − 2 x − 2 C n x \dfrac{C_{n-2}^{x-2}}{C_n^x} CnxCn−2x−2。
然后就是计算得分,发现只需要计算距离为幸运数的点对的个数即可。
点分治
最终答案乘上 C n − 2 x − 2 C n x = x ( x − 1 ) n ( n − 1 ) \dfrac{C_{n-2}^{x-2}}{C_n^x} = \dfrac{x(x-1)}{n(n-1)} CnxCn−2x−2=n(n−1)x(x−1)。
Noip2021模拟测试赛(三)
A 选举
首先想到贪心,发现不行。
那就 DP。考虑 f i f_i fi 代表 i i i 之前最大答案。然后发现 f i f_i fi 转移非常鬼畜,需要 O ( l − r ) O(l - r) O(l−r)。
f i = m a x j = l r ( f j + [ ∑ k = j + 1 i ] ) f_i = max_{j=l}^{r}\Big(f_j+\Big[\sum_{k=j + 1}^{i}\Big]\Big) fi=maxj=lr(fj+[k=j+1∑i])
额。。。那个 [ ] [] [] 就自行理解一下吧,主要是我不知道怎么表示
尝试优化。发现区间 [ j + 1 , i ] [j + 1, i] [j+1,i] 的和可以使用前缀和求出(一下称为 s s s)。
就变成了有关 s i s_i si 和 s j s_j sj 大小关系的式子。
那么我们开一个值域线段树,下标为 s i s_i si。
记录什么呢?节点 [ L , R ] [L,R] [L,R] 记录 [ i − l , i − r ] [i - l, i - r] [i−l,i−r] 内,每个 s j ∈ [ L , R ] s_j \in[L,R] sj∈[L,R] 的 f j f_j fj(所有 f j f_j fj,拿单调队列储存)
对于每个 i i i,我们在线段树上查询:
- s j ∈ ( − ∞ , s i ) s_j \in (-\infty,s_i) sj∈(−∞,si) 的最大 f j f_j fj
- s j = s i s_j = s_i sj=si 的最大 f j f_j fj
- s j ∈ ( s i , + ∞ ) s_j \in (s_i,+\infty) sj∈(si,+∞) 的最大 f j f_j fj。
就可以计算答案了。
时间复杂度 O ( n log n ) O(n\log n) O(nlogn)
B 蛋糕
欸欸额,这题要画图,先不写了吧。
可以自己推一下。
C 魔法树
被施了魔法的树就是点分树。
满足的条件是:每个节点都是其子树的重心。
或者: ∀ u , max v ∈ s o n u ( s i z v ) ≤ s i z u 2 \forall u, \max_{v\in son_u} (siz_v)\leq \dfrac{siz_u}{2} ∀u,maxv∈sonu(sizv)≤2sizu
Noip2021模拟测试赛(四)
A Dam
首先要明确一个东西:当天的水加进去后才能倒!
所以,这就导致了某些水必须融合。
我们开始贪心递推。
对于当天的水 ( t i , v i ) (t_i, v_i) (ti,vi),由于必须全部放进水池里,所以一定是把之前温度最小的体积总和为 v i v_i vi 的水倒掉。
我们已经将这些水踢出去了,你以为直接加入今天的水就可以了?其实事情远没有这么简单。
如果 t 1 > t 2 t_1 > t_2 t1>t2,我们现在要处理第三天的答案,发现水体积过多,所以我们要倒出部分水。
按照原来的思想,肯定要倒出 t i t_i ti 最低的水,所以我们要倒 t 2 t_2 t2 的,但是你会发现无法单独倒不出去。
我们要保留下第一天的所有水,但又要倒出第二天的水,怎么可能嘛。
所以我们要考虑水会融合的情况。
发现,只有当当天天水 t i t_i ti 比之前最高水温更低时才会融合,因为这个情况下,我们肯定想要保留更高的水温,但是要保留更高水温又只能融合。
假设当前队列是从小到大的(队尾最大),里面储存了一些没有融合的水,和一些融合的水。
那么我们每次加入水的时候,将队首的 v i v_i vi 的水倒掉(这时不需考虑是否融合,因为之前加入时已经考虑过了)。
这时考虑加入当天水。
我们先放在队尾,然后和原来队尾的比较,如果水温比队尾还要小,则合并(记录到当天水温),继续执行刚才的过程,直到原先队尾没有当天水温高。
B Flip and Rectangles
非常像一道经典 DP —— 最大全 1 1 1 子矩阵。
当然想着转换成这个问题啊。
容易发现 ,当且仅当一个 2 × 2 2 \times 2 2×2 的子矩阵中 1 1 1 的个数为偶数时,这个矩阵能被转换成全 1 1 1
还要证明吗?
首先, 1 1 1 的个数为奇数时肯定不行,因为每次修改一列或一行不更改奇偶性。
然后枚举 1 1 1 的个数为偶数时的方案
1 1 1 1 \begin{matrix}1&1\\1&1\end{matrix} 1111
0 0 1 1 → 1 1 1 1 \begin{matrix}0&0\\1&1\end{matrix} \to \begin{matrix}1&1\\1&1\end{matrix} 0101→1111
0 1 1 0 → 1 1 0 0 → 1 1 1 1 \begin{matrix}0&1\\1&0\end{matrix} \to \begin{matrix}1&1\\0&0\end{matrix} \to \begin{matrix}1&1\\1&1\end{matrix} 0110→1010→1111
0 0 0 0 → 1 1 0 0 → 1 1 1 1 \begin{matrix}0&0\\0&0\end{matrix} \to \begin{matrix}1&1\\0&0\end{matrix} \to \begin{matrix}1&1\\1&1\end{matrix} 0000→1010→1111
证明结束。
Noip2021模拟测试赛(五)
A 冷战
第一眼:什么 LCT 合并 + 树链剖分?
然后:并查集按秩合并 + 暴力?????
首先容易发现我们只需要把连边操作的边添加一个权值,为当前时间。
然后每次查询 u , v u, v u,v 两点间路径上最大边权就行了。
好吧确实 LCT 可以做,但看题解后我发现可以并查集按秩合并。
按秩合并可以保证树高 log \log log 级别,然后每个询问暴力寻找 l c a lca lca 和统计答案即可
B
Noip2021模拟测试赛(六)
A And Grid
构造大水题。
容易发现,我们只需要这样就行了:
#####
#.#.#
#.#.#
#.#.#
.....
.....
.#.#.
.#.#.
.#.#.
#####
记得补上原来图上自带的 #
B Connect?
大水题
对于每对点来说,只有两个点都处于边上的节点才有“威胁”。其他的随随便便都绕过去了
于是只记录这种节点。
如果记录下的点对存在交叉就代表不可行。
然后判断,先将每个节点按照顺时针(逆时针也行)排序,然后使用栈,对于当前节点,如果其编号在栈顶,就删除,否则加入栈。最后判断栈是否空即可(空了就代表可行)。
C
Noip2021模拟测试赛(七)
A Fountian Walk
观察题目你会发现一个离谱的事实:走 1 4 \frac{1}{4} 41 个喷泉比走拐角要快!
所以我们尽量多走拐角处的喷泉(在走最短路径的前提下)。
可以用单调队列来维护(队首低)。
还有一个特殊情况:必须走 1 2 \frac{1}{2} 21 喷泉。只会出现在最高的一行。
只需特判即可。
B Arrays and Palindromend Palindrome
鬼畜构造题
可以发现,如果当前 a i a_i ai 为偶数,可以有几种构造方式(连边代表相等,上面是 a a a 数组连的边,下面是 b b b):

其中,如果我们要将两个连续偶数连起来,可以使用其空出的位置:

a i a_i ai 为奇数则达不成第三种情况,只有两种构造:
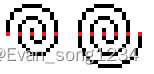
所以 a i a_i ai 为奇数时 i i i 只能为 1 1 1 或 n n n。
那么我们总结一下:
-
若 m = 1 m = 1 m=1: b = { 1 , m − 1 } b=\{1,m-1\} b={1,m−1}。
-
若 m > 1 m > 1 m>1:
- 若 a a a 出现三个以上奇数:不可行
- 若 a a a 出现两个奇数:分别放在头尾
- 若 a a a 出现一个奇数:放在头或放在尾
- 若 a a a 没有奇数:啥都不用干。
最终答案: b = { a 1 + 1 , a 2 , a 3 , a 4 , . . . , a n − 1 , a n − 1 } b = \{a_1+1,a_2,a_3,a_4,...,a_{n-1},a_n-1\} b={a1+1,a2,a3,a4,...,an−1,an−1}。
Noip2021模拟测试赛(八)
A Game on Tree
显然树形 DP。假设 f i f_i fi 为 i i i 的子树先手是否胜( 0 0 0:先手败)。
容易发现,如果一个节点 u u u 的儿子 v v v, f v = 1 f_v = 1 fv=1,就代表在 v v v 子树里,先手走完就变成后手了。反之,如果 f v = 0 f_v = 0 fv=0,就代表先手走完还是先手。
所以,在计算 f u f_u fu 时,我们可以把所有 f v = 1 f_v=1 fv=1 的节点 v v v,都当成只有一个儿子来计算。
然后就是经典问题了。
B Shift and Flip
可以想到,达成目标要两步:先将需要改变的位置更改,然后对齐 B B B。
一定是先往一个方向移动,然后反向,再移动过原位。
所以先预处理出每个点往左和往右移第一个遇到的 b i = 1 b_i = 1 bi=1,分别记为 l i , r i l_i, r_i li,ri。
然后我们可以考虑最终是右移对齐b的还是左移对齐b的。
以右移为例。 假如要 c n t cnt cnt 步。
如果我们需要更改的位置中,有 r i > c n t r_i > cnt ri>cnt 的位置,我们只能再右移长一点最后再左移回来,或尝试一开始左移至少 L L L 步。
也就是对于每一个这样的位置,都有两种选择。
如果全部选择第一种,那么在移动的步数上是最大左移步数 × 2 + c n t \times 2 + cnt ×2+cnt。
如果选择过右移满足,那么在移动的步数上是最大左移步数 × 2 + \times 2~+ ~ ×2 + 最大右移步数 × 2 − c n t \times2-cnt ×2−cnt。
我们可以枚举最大左移步数,然后找到对应的最大右移步数,计算最小答案。
只需要最小化移动步数就行了,翻转操作的次数是固定的(为对应对齐位置时 a a a 与 b b b 相差个数)。
C
Noip2021模拟测试赛(九)
A Manhattan Compass
你会发现这是一个 b f s bfs bfs 的过程,时间复杂度 O ( n + m ) O(n+m) O(n+m)
如果直接跑, n n n 显然没问题,但是 m m m 太大了,和 n 2 n^2 n2 同级。
考虑能否优化 m m m。
首先会发现能和一个点哈曼顿距离为一个固定值的点一定是在这上的:
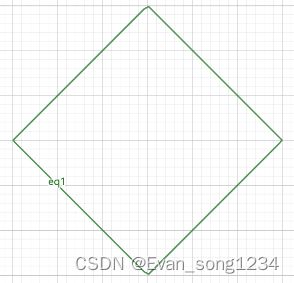
所以,我们对于左上的边,把所有点按照 ( x i − y i , x i + y i ) (x_i-y_i,x_i+y_i) (xi−yi,xi+yi) 二元组排序,然后二分枚举处于这条线上的左端点和右端点。其余三条边同理。
然后你发现有八个二分,玩nm
然后暴力 b f s bfs bfs 即可。
B BBQ Hard
发现对于两个整合包 i , j i, j i,j 把他们串到两个串上面不同的方式有 C a i + b i + a j + b j a i + a j C_{a_i+b_i+a_j+b_j}^{a_i+a_j} Cai+bi+aj+bjai+aj 种(在所有空里面选 a i + a j a_i+a_j ai+aj 个放牛肉)
于是答案就变成了: ∑ 1 = 1 n ∑ j = i + 1 n C a i + b i + a j + b j a i + a j \sum_{1=1}^{n}\sum_{j=i+1}^{n}C_{a_i+b_i+a_j+b_j}^{a_i+a_j} 1=1∑nj=i+1∑nCai+bi+aj+bjai+aj
我们知道,一个 n × m n\times m n×m 的方格图,只向下或右走,从左上角走到右下角的方案数为 C n + m n C_{n+m}^{n} Cn+mn
所以 C a i + b i + a j + b j a i + a j C_{a_i+b_i+a_j+b_j}^{a_i+a_j} Cai+bi+aj+bjai+aj 可以看成,一个 ( a i + a j ) × ( b i + b j ) (a_i+a_j)\times(b_i+b_j) (ai+aj)×(bi+bj) 的方格图,只向下或右走,从左上角走到右下角的方案数。
我们可以继续转换,放到坐标系上,即为:一个点 ( − a i , − b i ) (-a_i,-b_i) (−ai,−bi),只向上或向右走,走到 ( a j , b j ) (a_j,b_j) (aj,bj) 的方案数。
那么原问题 ∑ 1 = 1 n ∑ j = i + 1 n C a i + b i + a j + b j a i + a j \sum_{1=1}^{n}\sum_{j=i+1}^{n}C_{a_i+b_i+a_j+b_j}^{a_i+a_j} ∑1=1n∑j=i+1nCai+bi+aj+bjai+aj 就可以转换成:
从所有 ( − a i , − b i ) (-a_i,-b_i) (−ai,−bi) 中任意点开始,走到任意 ( a j , b j ) (a_j,b_j) (aj,bj) 为止的方案数。
就变成了 DP 题。
别忘了判重, ( − a i , − b i ) (-a_i,-b_i) (−ai,−bi) 的 i i i 和 ( a j , b j ) (a_j,b_j) (aj,bj) 的 j j j 不可以相等。
Noip2021模拟测试赛(十)
A Jigsaw
先将一个拼图拆分成两个已经拼起的拼图,分别为左边和右边。
对于左边,若 c i = 0 c_i = 0 ci=0,我们记录他的权值为 a i a_i ai,若 c i > 0 c_i > 0 ci>0,我们记录他的权值为 − c i -c_i −ci
对于右边,若 d i = 0 d_i = 0 di=0,我们记录他的权值为 − b i -b_i −bi,若 d i > 0 d_i > 0 di>0,我们记录他的权值为 d i d_i di
这时,如果两个拼图能够拼起来,则需要满足权值相同。
那么对于每一张拼图,我们把左边和右边的权值之间连边(左往右连有向边)。
我们尝试找出一条规律,使得满足这条规律的都可行,反之则不行。
对于 u > 0 u > 0 u>0 的节点,需要满足入度 i n u ≤ o u t u in_u\leq out_u inu≤outu。
对于 u < 0 u < 0 u<0 的节点,需要满足入度 i n u ≥ o u t u in_u\geq out_u inu≥outu。
对于任意联通块内点,需要满足 ∃ u , i n u ≠ o u t u \exist u,in_u\not=out_u ∃u,inu=outu
B Addition and Subtraction Hard
首先,括号只能加到减号后面。
其次,括号不能叠到三层以上。(第一层,一定是减号后括起来几个加号或减号。第二层,一定是减号后多个加号。)
于是直接 dp, f i , j f_{i,j} fi,j 代表第 i i i 个数字前,还剩下 j j j 个括号的情况。
然后可以推出式子:
若 a i a_i ai 前是加号:
f i , 0 = max ( f i − 1 , 0 + a i , f i − 1 , 1 + a i , f i − 1 , 2 + a i ) f i , 1 = max ( f i − 1 , 1 − a i , f i − 1 , 2 − a i ) f i , 2 = f i − 1 , 2 + a i f_{i,0} = \max(f_{i-1,0}+a_i,f_{i-1,1}+a_i,f_{i-1,2}+a_i)\\f_{i,1} = \max(f_{i-1,1}-a_i,f_{i-1,2}-a_i)\\f_{i,2}=f_{i-1,2}+a_i fi,0=max(fi−1,0+ai,fi−1,1+ai,fi−1,2+ai)fi,1=max(fi−1,1−ai,fi−1,2−ai)fi,2=fi−1,2+ai
若 a i a_i ai 前是减号:
f i , 0 = max ( f i − 1 , 0 − a i , f i − 1 , 1 − a i , f i − 1 , 2 − a i ) f i , 1 = max ( f i − 1 , 0 − a i , f i − 1 , 1 + a i , f i − 1 , 1 − a i , f i − 1 , 2 + a i ) f i , 2 = max ( f i − 1 , 1 + a i , f i − 1 , 2 − a i , f i − 1 , 2 + a i ) f_{i,0} = \max(f_{i-1,0}-a_i,f_{i-1,1}-a_i,f_{i-1,2}-a_i)\\f_{i,1} = \max(f_{i-1,0}-a_i,f_{i-1,1}+a_i,f_{i-1,1}-a_i,f_{i-1,2}+a_i)\\f_{i,2}=\max(f_{i-1,1}+a_i,f_{i-1,2}-a_i,f_{i-1,2}+a_i) fi,0=max(fi−1,0−ai,fi−1,1−ai,fi−1,2−ai)fi,1=max(fi−1,0−ai,fi−1,1+ai,fi−1,1−ai,fi−1,2+ai)fi,2=max(fi−1,1+ai,fi−1,2−ai,fi−1,2+ai)
温馨提醒:
- 可能出现添一个右括号又添一个左括号的情况:
( 1 - ( 1 + 1 ) - (1 + 1) - 1) - 可能出现连续添加两个右括号的情况:
( 1 - ( 1 + 1 ) )
C 情报传递
离线,对于一个询问,风险值 c i c_i ci,当前时间 t i t_i ti,只有时间在 t i − c i t_i - c_i ti−ci 前的修改,危险值才会超过 c i c_i ci。
所以相当于询问 t i − c i t_i - c_i ti−ci 时路径 ( u , v ) (u,v) (u,v) 上的和。
建立主席树,对每个节点 u u u,储存 ( 1 , u ) (1,u) (1,u) 上的和,然后差分。
Noip2021模拟测试赛(十一)
A xor
可以发现,对于每个连通块,如果答案不是 − 1 -1 −1,则确定一个点的值,其他点的值都能确定。而且每个联通块中编号最小的点的值可以随意确定。
所以我们对于每个连通块编号最小的点排序,从后往前推。
然后发现 k ≤ 100 k \leq 100 k≤100,所以不存在需要更改两个节点的值的情况。
最后一个编号最小的节点标为 k − 1 k - 1 k−1,然后前面的编号最小的节点全部标为 0 0 0。
推一遍,得出答案,冲突就是 − 1 -1 −1。
B
C
Noip2021模拟测试赛(十二)
A 字符串大师
容易发现,最短循环节长度 p e r i = i − n x t i per_i = i - nxt_i peri=i−nxti
所以我们相当于知道了 n x t i nxt_i nxti。我们可以从 n x t i nxt_i nxti 推出原字符串。
若 n x t i ≠ 0 nxt_i\not= 0 nxti=0,就代表 s 0 . . . s n x t i − 1 = s i − n x t i . . . s i − 1 s_{0}...s_{nxt_i-1} = s_{i - nxt_i} ... s_{i-1} s0...snxti−1=si−nxti...si−1。
若 n x t i = 0 nxt_i = 0 nxti=0,则意味着 n x t i − 1 nxt_{i-1} nxti−1、 n x t n x t i − 1 nxt_{nxt_{i-1}} nxtnxti−1 等的下一个字符都不等于当前字符。此时只需要循环向前重复找 n x t nxt nxt 的过程,并把下一个位置的字符设为不可选择即可。