移动端扫描APP解决方案(一)——使用传统图像处理方法提取与矫正拍照文档边缘
一、概述
1.拍照扫描应用
在日常办公中,使用手机拍照扫描文件是一种高效、环保的方式。通过手机扫描,可以将纸质文件转化为电子版,不仅减少了纸张的使用,还节省了时间和精力。扫描后的电子版文件可以方便地储存和管理,不必再担心文件的丢失或损坏。通过使用手机拍照扫描的功能,可以轻松地快速生成高质量的电子版文件,从而提高工作效率并确保文件的安全性。
现在很多手机都内置了拍照扫描并提取出文字的功能,也有很多做得很成功的APP,博主之前也参与开发过类似的APP,这些手机扫描工具都具有简单易用的界面和强大的功能,可以帮助使用者轻松完成文件扫描任务。
2.工程流程
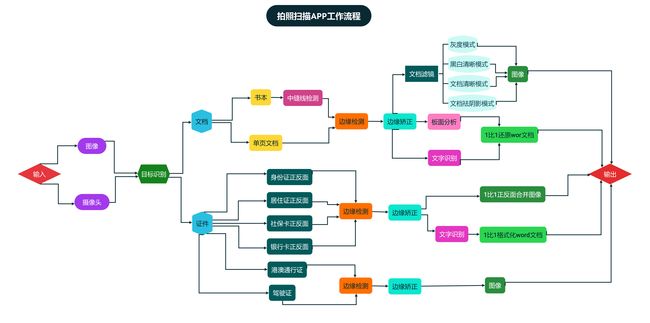
一般的文档拍照扫描App的工作流程通常包括以下步骤:
-
访问图像: 访问手机里面的图像。
-
访问相机: 应用程序请求用户授权,以访问设备的相机功能。
-
图像处理: 拍摄的照片会经过图像处理算法,以优化图像质量,去除背景噪音,调整亮度和对比度等,确保文档清晰可读。
-
边缘检测: 应用程序可能会使用边缘检测算法识别文档的边缘,以便更好地裁剪文档。
-
文档裁剪: 应用程序根据边缘检测的结果或用户指定的区域,裁剪图像以去除非文档部分,只保留需要的内容。
-
图像校正: 一些应用程序可能会对图像进行校正,以确保文档呈正常的方向,例如自动旋转或矫正倾斜。
-
图像压缩: 为了减小文件大小,一些应用程序可能会对图像进行压缩,以便更轻松地分享或存储。
-
识别文本: 应用程序使用光学字符识别(OCR)技术来识别图像中的文本,并将其转换为可编辑的文本格式。
-
保存输出: 用户可以选择将扫描的文档保存到设备上的特定位置,或者分享给其他人,例如通过电子邮件、云存储服务或即时消息应用。
具体流程图如下:
二、传统图像边缘检测
拍照扫描其中最主要的一环是,文档边缘检测与文档矫正,如果没有边缘检测与矫正,那之后的所有步骤都很难实现。边缘检测是计算机视觉中一个非常古老的问题,它涉及到检测图像中的边缘来确定目标的边界,从而分离感兴趣的目标。
1、边缘检测常用算法
传统图像处理中的边缘检测方法主要依赖于一些经典的滤波器和运算技术,大概有以下几种:
-
Sobel 操作: Sobel 操作是一种基于卷积的方法,通过在图像中应用Sobel算子(一种特殊的卷积核)来检测图像中的边缘。它在水平和垂直方向上分别进行卷积操作,然后将两个方向的结果合并。
-
Canny 边缘检测: Canny 边缘检测是一种多阶段的算法,包括噪声抑制、梯度计算、非极大值抑制和边缘跟踪等步骤。Canny 边缘检测在检测边缘的同时,对边缘进行细化,产生较为准确的结果。
-
Laplacian of Gaussian(LoG): LoG 算法首先对图像进行高斯平滑,然后应用拉普拉斯算子。这有助于检测图像中的变化,从而找到边缘。
-
Prewitt 操作: 类似于Sobel,Prewitt 算子也是一种卷积操作,用于检测图像中的垂直和水平边缘。
-
边缘增强滤波器: 一些特定的滤波器,如Roberts、Frei-Chen等,也可以用于边缘检测。
2、Canny边缘检测算法
Canny边缘检测是一种经典且广泛使用的边缘检测技术,已经成为计算机视觉领域中的主流方法之一,该算法由John Canny于1986年提出,被设计为一种多步骤的过程,以提取图像中的边缘,并在边缘上产生单像素的线条。
2.1 输入灰度图像
Canny算子只能对单通道灰度图像进行处理,
图像灰度是指将彩色图像中的每个像素点的颜色信息转换为相应的灰度值的过程。在灰度图像中,每个像素只有一个通道,表示图像的亮度。灰度值通常在0到255之间,其中0代表黑色,255代表白色。
转换彩色图像为灰度图像的一种常见方法是使用加权平均法,通过将彩色通道的颜色值按照一定的权重进行加权求和。一个常见的加权平均公式是:
灰度值 = 0.299 * 红色通道+ 0.587 *绿色通道 + 0.114 *蓝色通道
这个公式是根据人眼对不同颜色的敏感度来确定的,红色、绿色和蓝色通道的权重分别为0.299、0.587和0.114。
在很多图像处理库中,包括OpenCV都提供了直接将彩色图像转换为灰度图像的函数。例如,在OpenCV中,可以使用cvtColor函数。
2.2 滤波降噪处理
理想的图像具有无噪声、高质量的特点,然而在实际应用中,由于采集设备、环境干扰等多种原因,图像通常包含大量的噪声,其中最常见的是椒盐噪声和高斯噪声。高斯滤波通过卷积图像和高斯核来实现,这有助于去除图像中的高频噪声,提高后续边缘检测的稳定性。
在实际应用中,调整高斯滤波参数和阈值的选择对Canny算法的性能起着关键作用。这使得Canny算子成为处理噪声且要求高精度边缘检测的场景中的常用工具。这里也可以尝试使用双边滤波等算法。
高斯滤波使用的高斯核是具有 x 和 y两个维度的高斯函数,且两个维度上标准差一般取相同,形式为:
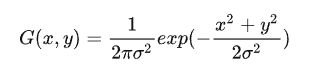
高斯滤波,即使用即使用某一尺寸的二维高斯核与图像进行卷积。由于数字图像的数据形式为离散矩阵,高斯核是对连续高斯函数的离散近似,通过对高斯曲面进行离散采样和归一化得出。例如,尺寸为 3X3,标准差为 1 的高斯核为:

在确定高斯核后,将其与图像进行离散卷积即可。高斯滤波可以将图像中的噪声部分过滤出来,避免后面进行边缘检测时将错误的噪声信息也误识别为边缘了。
2.3 计算像素梯度
在Canny算子中,梯度计算是通过一阶有限差分来实现的,而常用的梯度算子之一是Sobel算子。Sobel算子对图像进行卷积操作,分别计算图像在x和y方向上的梯度,从而得到两个梯度矩阵。
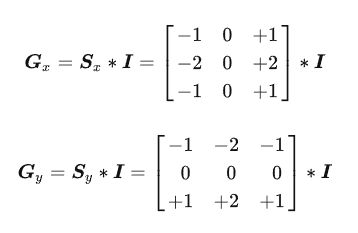
其中,I为灰度图像矩阵,且此处的 * 表示互相关运算(卷积运算可视为将卷积核旋转180°后的互相关运算)。需要说明的是,图像矩阵坐标系原点在左上角,且 x正方向为从左到右, y 正方向为从上到下。

可以计算得到梯度矩阵Gxy。
2.4 非极大值像素梯度抑制
非极大值像素梯度抑制是Canny边缘检测算法中的一个重要步骤,其目的是消除边缘检测带来的杂散响应,使得检测到的边缘更加精细,起到将边缘“瘦身”的作用。

如果上图表示,C表示为当前非极大值抑制的点,g1-4为它的8连通邻域点,图中蓝色线段表示上一步计算得到的角度图像C点的值,即梯度方向,第一步先判断C灰度值在8值邻域内是否最大,如是则继续检查图中梯度方向交点dTmp1,dTmp2值是否大于C,如C点大于dTmp1,dTmp2点的灰度值,则认定C点为极大值点,置为1,因此最后生成的图像应为一副二值图像,边缘理想状态下都为单像素边缘。
在非极大值抑制的过程中,需要注意的是,梯度方向的交点并不一定精确地位于8领域内的8个点的位置。因此,在实际应用中,为了获取更准确的梯度值,通常会使用相邻两个点的双线性插值所形成的灰度值。
具体而言,对于当前像素位置(x, y)以及垂直向上的梯度方向,找到梯度方向上的两个相邻点,例如(x, y-1)和(x, y+1)。然后,通过双线性插值计算这两个点之间的灰度值,考虑到相邻像素的权重,以更精确地估计灰度值。
这种插值的过程确保了在梯度方向上获得了更为准确的灰度信息。最终,在非极大值抑制后,选择梯度方向上的最大值作为边缘点,有助于形成细致而准确的单像素边缘。这个过程在图像处理中经常使用,特别是在涉及到子像素级别的信息时,以提高边缘检测的精度。在Canny算法中,这一步骤对于生成细致、准确的单像素边缘非常关键。
其中梯度方向均为垂直向上,经过非极大值抑制后取梯度方向上最大值为边缘点,形成细且准确的单像素边缘,如下图:

这个步骤的效果是保留具有局部最大梯度值的像素,从而实现了对边缘的细化,使得检测到的边缘更加准确。非极大值像素梯度抑制是Canny边缘检测算法中的关键步骤之一,有助于提高算法的精度和抗噪声能力。
2.5 滞后阈值
在Canny边缘检测的最后阶段,需要考虑哪些被检测到的边缘是真实的,哪些是虚假的。为了达到这个目的,引入了两个阈值,通常称为minVal(最小值)和maxVal(最大值)。
具体的处理流程如下:
- 对于每个像素,如果其梯度强度大于
maxVal,则将其标记为强边缘,这些点被确定为真实的边缘。 - 对于梯度强度介于
minVal和maxVal之间的像素,如果与强边缘相连(通过连通性),则也被标记为边缘,因为它们可能是真实的边缘的一部分。 - 对于梯度强度低于
minVal的像素,将其标记为非边缘,因为它们被认为是噪声或虚假的边缘。
这个阶段的目标是通过阈值的设定,准确地确定真实的边缘,同时通过考虑连通性,连接较弱的边缘部分,以防止由于噪声或图像细节引起的不连续边缘。
通过适当选择minVal和maxVal的值,可以调整Canny算法的敏感性,以适应不同图像和应用场景的需求。这一阶段的调优通常需要根据具体情况进行实验和调整,以获得满意的边缘检测结果。

3.边缘代码实现
void getCanny(cv::Mat &gray, cv::Mat &canny)
{
cv::Mat thres;
double high_thres = threshold(gray, thres, 0, 255, cv::THRESH_BINARY | cv::THRESH_OTSU), low_thres = high_thres * 0.5;
cv::Canny(gray, canny, low_thres, high_thres);
}
三、传统方法直线检测
在获取文档边缘之后,要对文档的边缘做直线检测,霍夫变换是一种经典的线检测算法,它通过将图像中的点映射到参数空间中的线来实现。该算法具有检测任意方向的线段的能力,并且在处理具有大量噪声的图像时表现良好。
1. 霍夫空间和边缘点到霍夫空间的映射
霍夫空间是一个二维平面,其水平轴表示线的斜率(坡度),而垂直轴表示直线在边缘图像上的截距。在这个空间中,边缘图像上的一条线可以用 (y = ax + b) 的形式表示(Hough,1962年)。每一条直线在霍夫空间上对应于该直线的斜率 (a) 和截距 (b)。
具体而言,边缘图像上的一条线会在霍夫空间上产生一个点,因为该线的特征可以用斜率 (a) 和截距 (b) 来唯一确定。相反,边缘图像上的单个边缘点 ((xᵢ, yᵢ)) 可以通过无数条直线。因此,在霍夫空间中,这些边缘点以 (b = axᵢ + yᵢ) 的形式生成一条线(Leavers,1992)。
在霍夫变换算法中,霍夫空间的主要目的是确定边缘图像中是否存在直线。通过在霍夫空间中累积边缘图像上的点,可以找到在图像中表示共线的直线。这使得霍夫变换成为一种强大的线检测工具,可以应用于各种方向的直线检测,而不需要事先知道直线的方向。

使用 (y = ax + b) 形式的直线和带有斜率和截距的霍夫空间表示方式存在一个缺陷。在这种形式下,该算法无法有效检测垂直线,因为对于垂直线,斜率 (a) 是不确定的,可能是无穷大(Leavers,1992)。在编程中,这意味着计算机将需要无限量的存储空间来表示所有可能的斜率值。
为了避免这个问题,可以使用一种更适合垂直线的表示方式。一条直线可以由一条称为法线的线表示,该线穿过原点并垂直于该直线。法线的标准形式为 ρ = x cos( θ )+ y sin( θ ),其中ρ 是法线的长度,θ 是法线与 x 轴之间的角度。
这种表示方式的优势在于,对于所有可能的直线,都可以使用相对较小的参数空间来表示,从而减小了计算和存储的复杂性。通过使用法线表示,霍夫变换可以更全面地检测图像中的直线,包括垂直线。
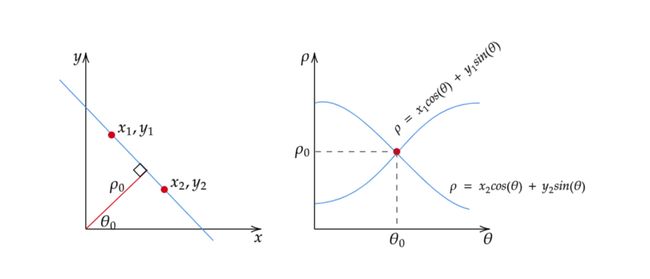
通过使用霍夫空间的极坐标表示ρ和θ,而不再使用斜率 (a) 和截距 (b),我们可以更有效地表示直线,并解决在处理垂直线时斜率 (a) 的无限值问题。在这种表示下,水平轴表示 (\theta) 值,垂直轴表示ρ值。
在这种情况下,边缘点到霍夫空间的映射仍然遵循相似的原理,但现在边缘点 ((x, y)) 在霍夫空间中生成的是余弦曲线,而不再是直线(Leavers,1992)。具体而言,边缘点 ((x, y)) 对应于在霍夫空间中以ρ = x cos( θ )+ y sin( θ )形式表示的余弦曲线。
这种正弦曲线的表示方式通过消除了在处理垂直线时斜率 (a) 的无限值问题,使得霍夫变换更加稳健。这样,霍夫变换可以更全面地检测图像中的直线,并且通过在极坐标中表示,也更容易在计算中处理。
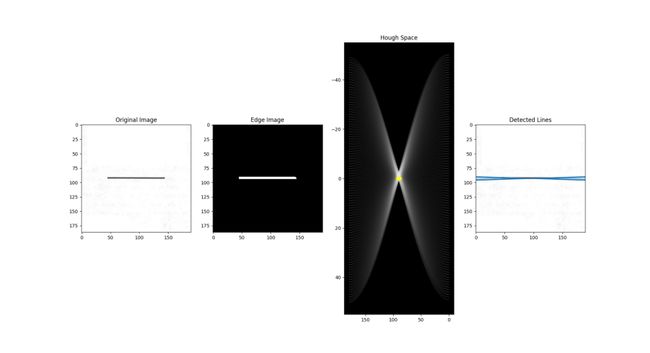
边缘点在霍夫空间中产生余弦曲线。如果将边缘图像中的所有边缘点映射到霍夫空间上,将会生成许多余弦曲线。当两个边缘点位于同一条直线上时,它们对应的余弦曲线将在特定的 (ρ,θ) 对上相互交叉。因此,霍夫变换算法通过找到在霍夫空间中交叉点数量大于某个阈值的 (ρ,θ) 对来检测直线。
需要注意的是,如果不对霍夫空间进行预处理,比如邻域抑制,以去除边缘图像中的相似线条,那么这种阈值化方法可能不会总是产生最佳结果。在一些情况下,可能会出现多个交叉点,使得检测到的直线数量较多。因此,根据具体应用,可能需要对霍夫空间进行进一步的处理,以提高算法的鲁棒性和准确性。这可以包括使用非极大值抑制或其他技术来优化霍夫变换的输出。
2. 算法实现
确定ρ 和θ 的范围是霍夫变换中的重要步骤。通常情况下,θ的范围是 [0, 180] 度,而ρ 的范围是 ([-d, d]),其中 (d) 是边缘图像对角线的长度。这种范围的量化意味着我们在霍夫空间中有了有限数量的可能值。
-
创建一个称为累加器的二维数组,表示霍夫空间的维度为(num_rhos,num_thetas)。初始化累加器中的所有值为零。
-
对原始图像执行边缘检测。可以使用选择的任何边缘检测算法来完成这一步。
-
对于边缘图像上的每个像素,检查该像素是否为边缘像素。如果是边缘像素,则循环遍历所有可能的ρ 值,计算对应的 θ,在累加器中找到 θ和 ρ的索引,并递增累加器中对应的值。
-
循环遍历累加器中的所有值。如果某个值大于某个阈值,则获取 ρ和 θ 的索引,从索引对中获取对应的 ρ和 θ的值。然后,可以将这些值转换回 (y = ax + b) 的形式。
3.代码实现
cv::Mat gray, canny, edge;
cvtColor(img_proc, gray, cv::COLOR_BGR2GRAY);
get_canny(gray, edge);
//二值化
binaryImage(edge, canny);
if (debug)
{
imshow("二值图像", canny);
}
//从边缘图像中提取线条
std::vector<cv::Vec4i> lines;
std::vector<Line> horizontals, verticals;
///第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
///第二个参数,InputArray类型的lines,经过调用HoughLinesP函数后后存储了检测到的线条的输出矢量,每一条线由具有四个元素的矢量(x_1, y_1, x_2, y_2) 表示,其中,(x_1, y_1)和(x_2, y_2) 是是每个检测到的线段的结束点。
///第三个参数,double类型的rho,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。
///第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
///第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。
///第六个参数,double类型的minLineLength,有默认值0,表示最低线段的长度,比这个设定参数短的线段就不能被显现出来。
///第七个参数,double类型的maxLineGap,有默认值0,允许将同一行点与点之间连接起来的最大的距离。
HoughLinesP(canny, lines, 1, CV_PI / 180, 100, 100, 20);
四、整体代码实现
#include "DocumentCorrection.h"
struct Line
{
cv::Point _p1;
cv::Point _p2;
cv::Point _center;
Line(cv::Point p1, cv::Point p2)
{
_p1 = p1;
_p2 = p2;
_center = cv::Point((p1.x + p2.x) / 2, (p1.y + p2.y) / 2);
}
};
void get_canny(cv::Mat& gray, cv::Mat& canny)
{
cv::Mat thres;
double high_thres = threshold(gray, thres, 0, 255, cv::THRESH_BINARY | cv::THRESH_OTSU), low_thres = high_thres * 0.5;
cv::Canny(gray, canny, low_thres, high_thres);
}
bool cmp_y(const Line &p1, const Line &p2)
{
return p1._center.y < p2._center.y;
}
bool cmp_x(const Line &p1, const Line &p2)
{
return p1._center.x < p2._center.x;
}
cv::Point2f computeIntersect(Line &l1, Line &l2)
{
int x1 = l1._p1.x, x2 = l1._p2.x, y1 = l1._p1.y, y2 = l1._p2.y;
int x3 = l2._p1.x, x4 = l2._p2.x, y3 = l2._p1.y, y4 = l2._p2.y;
if (float d = (x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4))
{
cv::Point2f pt;
pt.x = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / d;
pt.y = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / d;
return pt;
}
return cv::Point2f(-1, -1);
}
void binaryImage(cv::Mat &src, cv::Mat &dst)
{
int maxVal = 205;
int blockSize = 33;
double C = 0;
//adaptiveThreshold(src, dst, maxVal, cv::ADAPTIVE_THRESH_GAUSSIAN_C, cv::THRESH_BINARY, blockSize, C);
threshold(src, dst, 55, 255, cv::THRESH_BINARY);
}
void correction(cv::Mat &src, cv::Mat &dst, bool debug)
{
cv::Mat img_proc = src.clone();
int w_proc = src.size().width;
int h_proc = src.size().height;
cv::Mat img_dis = img_proc.clone();
cv::Mat gray, canny, edge;
cvtColor(img_proc, gray, cv::COLOR_BGR2GRAY);
get_canny(gray, edge);
//二值化
binaryImage(edge, canny);
if (debug)
{
imshow("二值图像", canny);
}
//从边缘图像中提取线条
std::vector<cv::Vec4i> lines;
std::vector<Line> horizontals, verticals;
///第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
///第二个参数,InputArray类型的lines,经过调用HoughLinesP函数后后存储了检测到的线条的输出矢量,每一条线由具有四个元素的矢量(x_1, y_1, x_2, y_2) 表示,其中,(x_1, y_1)和(x_2, y_2) 是是每个检测到的线段的结束点。
///第三个参数,double类型的rho,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。
///第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
///第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。
///第六个参数,double类型的minLineLength,有默认值0,表示最低线段的长度,比这个设定参数短的线段就不能被显现出来。
///第七个参数,double类型的maxLineGap,有默认值0,允许将同一行点与点之间连接起来的最大的距离。
HoughLinesP(canny, lines, 1, CV_PI / 180, 100, 100, 20);
for (size_t i = 0; i < lines.size(); i++)
{
cv::Vec4i v = lines[i];
double delta_x = v[0] - v[2];
double delta_y = v[1] - v[3];
Line l(cv::Point(v[0], v[1]), cv::Point(v[2], v[3]));
//得到水平线
if (fabs(delta_x) > fabs(delta_y))
{
horizontals.push_back(l);
}
//得到垂直线
else
{
verticals.push_back(l);
}
// for visualization only
if (debug)
{
line(img_proc, cv::Point(v[0], v[1]), cv::Point(v[2], v[3]), cv::Scalar(0, 0, 255), 1, cv::LINE_AA);
}
}
if (debug)
{
cv::namedWindow("line", 0);
imshow("line", img_proc);
}
// 检测不到全部边缘时的处理方式
if (horizontals.size() < 2)
{
if (horizontals.size() == 0 || horizontals[0]._center.y > h_proc / 2)
{
horizontals.push_back(Line(cv::Point(0, 0), cv::Point(w_proc - 1, 0)));
}
if (horizontals.size() == 0 || horizontals[0]._center.y <= h_proc / 2)
{
horizontals.push_back(Line(cv::Point(0, h_proc - 1), cv::Point(w_proc - 1, h_proc - 1)));
}
}
if (verticals.size() < 2)
{
if (verticals.size() == 0 || verticals[0]._center.x > w_proc / 2)
{
verticals.push_back(Line(cv::Point(0, 0), cv::Point(0, h_proc - 1)));
}
if (verticals.size() == 0 || verticals[0]._center.x <= w_proc / 2)
{
verticals.push_back(Line(cv::Point(w_proc - 1, 0), cv::Point(w_proc - 1, h_proc - 1)));
}
}
// 按线的中心坐标排序
std::sort(horizontals.begin(), horizontals.end(), cmp_y);//垂直
sort(verticals.begin(), verticals.end(), cmp_x);//水平
//画边缘的四条线
if (debug)
{
line(img_proc, horizontals[0]._p1, horizontals[0]._p2, cv::Scalar(0, 255, 0), 2, cv::LINE_AA);
line(img_proc, horizontals[horizontals.size() - 1]._p1, horizontals[horizontals.size() - 1]._p2, cv::Scalar(0, 255, 0), 2, cv::LINE_AA);
line(img_proc, verticals[0]._p1, verticals[0]._p2, cv::Scalar(255, 0, 0), 2, cv::LINE_AA);
line(img_proc, verticals[verticals.size() - 1]._p1, verticals[verticals.size() - 1]._p2, cv::Scalar(255, 0, 0), 2, cv::LINE_AA);
cv::namedWindow("检测线", 0);
cv::imshow("检测线", img_proc);
}
/*透视变换*/
//设置校正后的图像大小
int w_o = src.size().width;
int h_o = src.size().height;
dst = cv::Mat::zeros(h_o, w_o, CV_8UC3);
std::vector<cv::Point2f> dst_pts, img_pts;
dst_pts.push_back(cv::Point(0, 0));
dst_pts.push_back(cv::Point(w_o - 1, 0));
dst_pts.push_back(cv::Point(0, h_o - 1));
dst_pts.push_back(cv::Point(w_o - 1, h_o - 1));
//原图对应的检测到的交叉点
img_pts.push_back(computeIntersect(horizontals[0], verticals[0]));
img_pts.push_back(computeIntersect(horizontals[0], verticals[verticals.size() - 1]));
img_pts.push_back(computeIntersect(horizontals[horizontals.size() - 1], verticals[0]));
img_pts.push_back(computeIntersect(horizontals[horizontals.size() - 1], verticals[verticals.size() - 1]));
// 转换为原图的比例
for (size_t i = 0; i < img_pts.size(); i++)
{
if (debug)
{
circle(img_proc, img_pts[i], 10, cv::Scalar(255, 255, 0), 3);
cv::namedWindow("校正点", 0);
cv::imshow("校正点", img_proc);
}
}
//得到变换矩阵
cv::Mat transmtx = getPerspectiveTransform(img_pts, dst_pts);
//视角转换
warpPerspective(src, dst, transmtx, dst.size());
if (debug)
{
cv::namedWindow("dst", 0);
cv::imshow("dst", dst);
cv::waitKey();
}
}