【0基础教程】小学数学水平就能看懂的A星寻路算法详解（附Go代码）

一、概述

A星 (A-Star) 寻路算法常用于游戏编程，比如说向角色下达了移动指令后，它怎么从起点运动到终点，又或者控制NPC从一个地方走到另一个地方等等。

本文参阅了 Myopic Rhino 的这篇文章：
https://www.gamedev.net/reference/articles/article2003.asp
中译版：
https://blog.csdn.net/weixin_44489823/article/details/89382502

原文中只提及了算法的思想但没有具体代码实现，因此具体实现起来还是有一些坑要填。本文尽量采用最浅显的语言来表达，尽管略显啰嗦但保证大家都能读懂，事实上A星算法本身并没有包含太多数学理论，因此我相信理解它对大部分人来说还是很容易的。

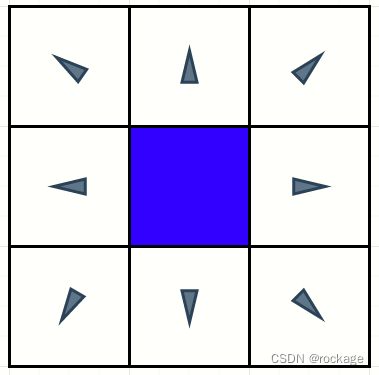
首先，A星算法是建立在一种格子(Grid)体系内的寻路机制。它将地图切分为一个个小格子，通过计算每个格子的权重来决定路径的走向，现在想象一下我们熟悉的数字九宫格，中间的 "5"号键被旁边的8个数字所包围，这8个数字代表8个方向，那么到底选择哪个方向运动呢？这就是A星算法要做的事情。

---

二、基本概念

• G、H、F

  整个A星算法围绕着G、H、F这3个参数做运算，他们的定义非常简单，比如下图，有一个起点格和终点格，还有一个格子P:

  G 表示P到起点的距离；

  H 表示P到终点的距离；

  F 表示两者之和，即G+H。

---

三、算法详解

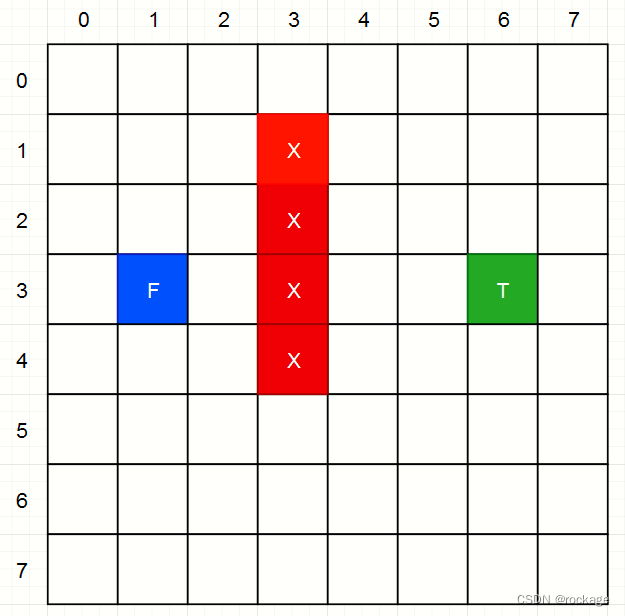
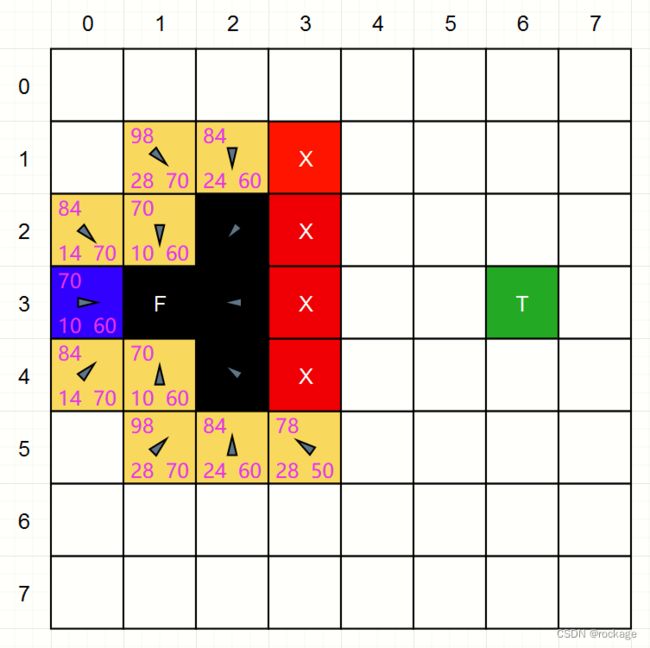
我们以一个8*8的地图为例, F 代表起点(From), T代表终点(To)，中间的红色方块是 ”墙“ ，也就是不能通过的地方，现在就一步一步的用A星算法来看看它到底是如何从F走向T的。

---

第一轮：

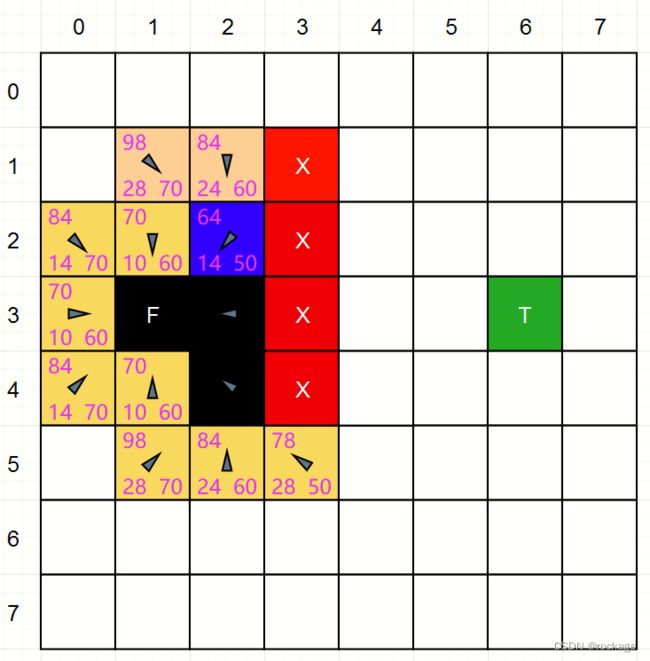
我们从起点F （1，3）开始，与它相邻的 ”邻居方块“ 我们用黄色表示，还记得前面说过的九宫格吗？是的，整个A星算法就是按照九宫格的方式来运作的。

与之相邻的黄色方块中，每个方块里有3个数字，这3个数字就是前面讲过的G、H、F值，其中左下角表示G值（与起点的距离），右下角表示H值（与终点的距离），至于F，很简单，就是G+H。至于值的具体运算，我们规定：

• 平移1格记作10；

• 斜移1格（即以对角线方式移动）记为14。

为什么会选择14这个数字，是因为我们直接取根号2的近似值做整数运算，避免了真正在算法里做算法平方根的操作，效率会大大提升。

比如以（2，4）这个格子为例，它的G是14（向左上斜移一格到达起点），它的H是50，表示从（2, 4) 移动到终点 T （6, 3）需要平移 5 次。

注意：在计算H值的时候，我们采用的是所谓的 ”曼哈顿距离“ （Manhattan Distance），就是说只考虑平移，不做斜移操作。（在纽约曼哈顿，你从一个街区走到另一个街区只能平移过去而不能穿建筑物而过因此得名）

此外：计算H是忽略了障碍物（”墙“）的存在的，H是对剩余距离的估算值，而不是实际值，A星算法本质上就是对终点的不断逼近而最终寻找出路径的。

除了这3个数字之外，每个黄色格子还有一个黑色的箭头，它的指向表示了他的 ”父方块“ 是谁，很显然，因为现在是第一轮，所以现在这 8 个黄色的父方块（或者说父结点）都是 F。

---

第二轮：

现在是第二轮，位于起点左边的方格（2，3）变成了蓝色，而上一轮的起点方格则变黑了，下面来解释一下这个变化的内在逻辑。在上一轮中，F 值最小（F=50）的黄色格子是 (2, 3) ，因此它被选中作为这一轮的处理格子，在接下来的每一轮都是这样。先确定邻居格（例子中的黄色方格），然后计算出他们的GHF值。最后，看看所有黄色的格子哪一个的 F 值最小，注意并非是本轮产生的邻居格，而是检查所有黄色格子里的F值，将最小的定位为下一轮筛选的处理格。

起点格（1，3）现在变黑了，是因为每一个处理完毕的格子，以后的每一轮均不再使用。所以我们需要维护一个数组称为 closeList, 将所有已经处理后的格子都存进去不再使用。

相应的，所有的黄色格子也需要一个数组去维护，我们称之为 openList, 每一轮只有一个格子被选中作为下一轮的处理格，而未被选中的格子会被放入 openList 中暂存。

请观察一下当前格（2，3），以它为中心的8个格子左边三个是红色的墙，忽略不计，左边的是黑色格子（1，3），已经被放入了 closeList，前面说过所有被置入closeList的格子都不再处理，因此也忽略不计。需要处理的是剩下的四个黄色格子：(1，2) 、(2，2)、（1，4）（2，4），事实上这4个格子在上一轮已经被放入了openList。现在需要做的是选中其中F值最小的做为下一轮的处理格。这时候分歧产生了，因为有两个格子的F=64 （2，2）和（2，4），那么我们应该怎么选呢？答案是无需理会，简单地以最后加入的那个为准就行了，观察图片，你会发现在F值相等的时候会发生路径分叉的情况。 A星算法并没有那么高的智能去判断是向上走还是向下走更好，只能硬选一条然后再不断逼近。

还有一点需要特别讨论一下，就是在处理这种已经纳入了 openList 的格子时，还需要注意它与起点距离（G值）是否比通过当前格产生的G值还大。这句话听上去十分拗口，我们还是用图片来加以说明，比如这种情况：

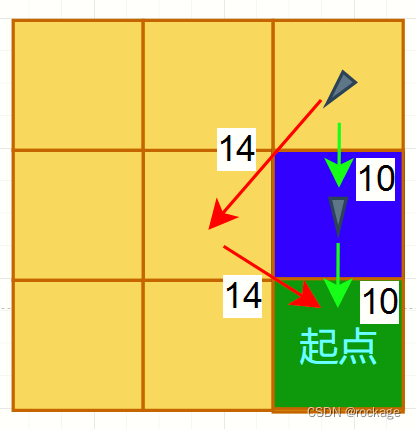
观察上图，右上角这个方块它的G值是14，意味着只需要斜移一格可以到达起点（图中用红色箭头表示）。 如果它改道通过当前方块（紫色方块），G值会是20，因为要移动两次才能抵达起点（图中用绿色箭头表示），很显然 14 < 20，说明这个格子按照原本的路径走就是最优的，这种情况下我们啥也不用做，直接忽略就好。 再来看一个反例：

还是右上角那个格子，但是起点不同了，如果按照它旧的路线，需要斜移两次才能达到起点，G值是28。但如果它改走经过当前格（紫色格子）的话，仅需平移两次，G值是20。显然 28 > 20，所以我们要修改它的父格子指针，让它指向当前格，如图：

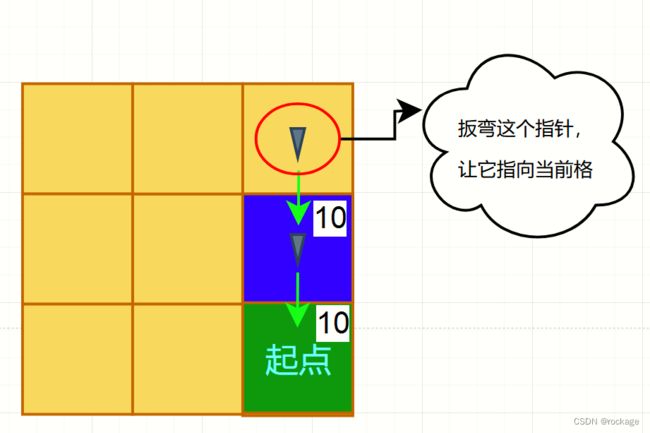
我看到很多留言，很多人对这个知识点有疑惑，但这不是理解的问题，而是用语言表达这个概念有些吃力，结合这三张图，我想还是很容易明白的。废话不多说，回到我们的案例。

---

第三轮：

第三轮，当前处理格是（2，4），以它为九宫格的中心，墙无需处理，两个黑色的已经被置入 closeList 的格子也不用处理，它的左边（1，4）是已经被纳入 openList 的格子，G值是10。而如果改走通过当前格的路径，G值会变成10+14 = 24，显然没必要这么做，因此也忽略。它的下方，新开辟了3个没有纳入 openList 的格子（注意我特意改了一下颜色略有不同），处理这种新开出来的格子很简单，只需要分别计算他们的G、H、F值，然后把他们的父格子指针指向当前格就行了（如图）。

---

第四轮：

这一轮除了新开了两个格子之外，没有太大变化。

第五轮：

这一轮来到了G=70的格子（0，3），它的左边是边界，因此既没有新格子可开，周边已经开过的格子G值也不用修改，风平浪静的一轮。

---

第六轮：

注意：这一轮产生了前面提到过的那种已经存在于openList中的格子的G值比改走当前格更大那种情况，请仔细分析本轮。

观察格子（1，1）本轮和上轮的变化，你会发现它的指针改变了。因为如果从（1，1）出发，按照原路径需要借道（2，2）然后再到起点F，这需要两次斜移（G值为28）。但是，如果经由（1，2）的话，则只需要两次平移（G值为20），因此将它的指针指向当前格。至此，关于A星算法在寻径过程中有可能会发生的情况基本上就这些了，接下来我只放一张总图，就不废话了，请诸位看官自行分析。

白色文字表示A星算法开图的顺序，当终点也被 openList 置入之后，说明存在一条从起点到终点的通路。但是我们如何确定路径呢？很简单，我们从终点开始反推每一个结点的父节点就可以了（图中用红色箭头表示反推的过程）。因为每一个结点只有一个确定的父节点，因此在探路过程中曾经使用过但有最终又没能成为路径的结点将会被略过。

想象一下，假设我们用墙把通路全部堵死，算法就会在openList中不停地去寻找下一个可能的路径，当 openList 中的元素全部耗尽的时候，说明无路可走。因此，寻路算法的终止条件有两条：

1、openList 中是否包含了终点？（找到了路径）

2、openList 是否为空？（没有路径）

---

四、代码实现

相信如果你能耐心看到这里，已经差不多可以手撸代码了，但是还有几个小坑需要填一下。首先是G值的计算问题，在讨论这个问题之前，我们先看看距离公式这个话题，常用的距离公式有以下3种：

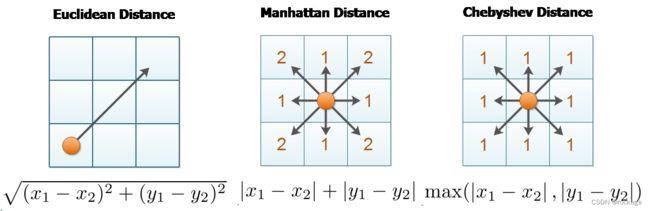
• 曼哈顿距离 (Manhattan distance)

  在前面我们曾经提到过 “曼哈顿距离”，是指一种只能上下左右做移动不能以对角方式移动的方式，移动1次记为1。

• 切比雪夫距离(Chebyshev distance)

  切比雪夫与曼哈顿距离很相似，它在概念上允许斜线的存在，但是它将移动1格直线或斜线都等同为距离1。

• 欧几里得距离(Eudidean distance)：

  它是两个点在坐标系中的真实距离，缺点是需要做算术平方根运算。

  以下是三种距离公式的差异：

---

那么问题来了，我们在计算G的时候，需要将斜线记作14，直线记作10，这是一种避免让系统做算术平方根的伪 “欧几里得距离”。因为两点间的平移距离为1，那么它的对角距离就是根号2（值是1.414）， 又为了避免出现浮点数，我们在它的近似值1.4的基础上再乘10，那么相应的，平移也需要等比例放大（1x10=10），这就是为什么我们选取10和14作为距离常数的原因。此外，我们还要设计一个这种伪“欧几里得距离”的算法，下面是代码：

func calculate_G(p1 Point, p2 Point) int {
    dx := math.Abs(float64(p1.x - p2.x))
    dy := math.Abs(float64(p1.y - p2.y))
    straight := int(math.Abs(dx - dy))
    bias := int(math.Min(float64(dx), float64(dy)))
    distance := straight*10 + bias*14
    return distance
}

方法是先取得两点间的曼哈顿距离，然后用较小的那个值乘14，用dx和dy的差值乘10就可以了。代码是用Golang写成的，但因其逻辑非常简单，基本上与语言无关。

其次是排序问题，还记得前面说过，每一轮结束的时候，需要从openList中找出一个F值最小的方块来作为下一轮的处理方块吗？尽管选择哪种排序算法并不会影响最终结果，但是效率却相差很大。一开始为了省事我用的是冒泡法，后来改用了二叉堆，结果效率至少提高了5倍。以下是二叉堆排序算法：

// 寻找list中的最小结点（二叉堆方法）
func findMin_Heap(tree []Node) Node {
    var n = len(tree) - 1
    // 建小根堆 (percolate_down)
    for i := (n - 1) / 2; i >= 0; i-- {
        percolate_down(tree, n, i)
    }
    return tree[0]
}
// 建堆（下滤）
func percolate_down(tree []Node, size int, parent_node int) {
    left_node := 2*parent_node + 1
    right_node := 2*parent_node + 2

    var max_node = parent_node
    if left_node <= size && tree[left_node].f < tree[parent_node].f {
        max_node = left_node
    }
    if right_node <= size && tree[right_node].f < tree[max_node].f {
        max_node = right_node
    }

    if max_node != parent_node {
        tree[parent_node], tree[max_node] = tree[max_node], tree[parent_node]
        percolate_down(tree, size, max_node)
    }
}

实际上二叉堆排序需要两个步骤，首先是建堆，然后才是排序。但在我们这个场景中我们并不需要真正排序，而只需要能把最小值取出来就可以了，二叉堆在建堆的时候就已经能保证最小值位于堆顶，尽管整个堆还是无序的，但它能保证链表中的第一个值是最小值即可，效率很高，所以A星算法搭配二叉堆是首选。

但是如果你不太明白二叉堆原理的话，就不是三言两语能讲清楚的了，这里有一篇我的博文可供参考：

二叉堆及堆排序详解保姆级教程略显罗嗦但保证能看懂_二叉堆排序_rockage的博客-CSDN博客

代码方面其他就没有什么可说的了，重要的是维护好 openList 和 closeList 这两个数组，每一轮寻径都有可能对这两个数组进行增删改的操作，是整个算法的核心。下面是整体运行流程：

1. 将起点放入 openList， 让它成为第一个 “当前格” ，寻路开始

2. 将当前格放入 closeList 中，保证下一轮不会被处理

3. 以当前格为中心，计算包裹它的8个邻居格的G、H、F，如果：

   • 邻居格越出地图边界 -> 忽略

   • 邻居格位于障碍物（墙） -> 忽略

   • 邻居格已经存在于 closeList 中 -> 忽略

   • 邻居格是新方格，不在 openList 中：

     • 计算其 G、H、F值，并将其父格子设为当前格。

   • 邻居格不是新方块，本身已经存在于 openList 中：

     • 计算其到起点的G值，如果小于经由当前格所产生的G值的话 -> 忽略

     • 如果大于经由当前格所产生的G值：

       • 将这个邻居格的父格子修改为当前格，并更新G、F值

4. 处理所有符合条件的邻居格，并存入 openList

5. 当8个方向都探测并计算完毕后，从 openList 中选出一个 F 值最小的格子，本轮结束

6. 将上一轮选出的 F值最小的格子设为新一轮的 “当前格”

7. 重复 2-6 步

8. 循环结束判定

   每一轮寻路结束后，需要对openList 进行判断：

   1. 终点已被包含在 openList 中，说明找到路径了，从终点开始，根据其父结点开始反推路径，程序结束。

   2. openList 中的元素为0，说明寻不到路径，程序结束。

package main

import (
	"fmt"
	"math"
	"time"
)

type Point struct {
	x int
	y int
}

type Node struct {
	coordinate Point
	parent     *Node
	f, g, h    int
}

// 地图大小
const cols = 8
const rows = 8

func main() {

	// 创建起点和终点 （F=From T=To)
	F := Point{1, 3}
	T := Point{6, 3}

	var obstacle []Point
	// 创建障碍
	obstacle = append(obstacle, Point{3, 1})
	obstacle = append(obstacle, Point{3, 2})
	obstacle = append(obstacle, Point{3, 3})
	obstacle = append(obstacle, Point{3, 4})

	// 创建地图
	var preMap [cols][rows]byte
	for y := 0; y <= rows-1; y++ {
		for x := 0; x <= cols-1; x++ {
			preMap[x][y] = 46 // 用字符 . 表示
		}
	}

	// 在地图上标记起点与终点
	preMap[F.x][F.y] = 70 // 字符 F = From
	preMap[T.x][T.y] = 84 // 字符 T = To

	// 在地图上标记障碍
	for _, v := range obstacle {
		preMap[v.x][v.y] = 88 // 用字符 X 表示
	}

	// 打印初始地图
	for y := 0; y <= rows-1; y++ {
		for x := 0; x <= cols-1; x++ {
			fmt.Printf("%c", preMap[x][y])
		}
		fmt.Printf("\n")
	}

	path := A_Star(preMap, F, T) // 开始寻径

	if path != nil { // 如找到路径则再次打印它：
		fmt.Println()
		fmt.Println("The path is as follow: ")
		// 在地图上标记障碍
		for _, v := range path {
			preMap[v.x][v.y] = 42 // 用字符 * 表示
		}
		for y := 0; y <= rows-1; y++ {
			for x := 0; x <= cols-1; x++ {
				fmt.Printf("%c", preMap[x][y])
			}
			fmt.Printf("\n")
		}
	}
}

// A*寻路主函数 preMap=地图 F=起点 T=终点
func A_Star(preMap [cols][rows]byte, F Point, T Point) []Point {
	var openList []Node
	var closeList []Node

	findPath := func() {
		//遍历 open list ，查找 F 值最小的节点，把它作为当前要处理的节点。
		curNode := findMin_Heap(openList)

		closeList = append(closeList, curNode)   // 将当前结点放入 closeList 中
		openList = deleteNode(openList, curNode) // 将 当前结点 从 openList 中删除

		// 遍历检测相邻节点的8个方向：NW N NE / W E / SW S SE
		direction := []Point{{-1, -1}, {0, -1}, {1, -1}, {-1, 0}, {1, 0}, {-1, 1}, {0, 1}, {1, 1}}

		for _, v := range direction { // 遍历基于父节点的8个方向
			var neighbour Node
			neighbour.coordinate.x = curNode.coordinate.x + v.x
			neighbour.coordinate.y = curNode.coordinate.y + v.y

			// 1. 是否超越地图边界?
			if (neighbour.coordinate.x < 0 || neighbour.coordinate.x >= cols) ||
				(neighbour.coordinate.y < 0 || neighbour.coordinate.y >= rows) {
				continue
			}

			// 2. 是否障碍物?
			if preMap[neighbour.coordinate.x][neighbour.coordinate.y] == 88 { // 88 = 字符 'X'
				continue
			}

			// 3. 自身是否已经存在于 closeList 中？
			if existNode(neighbour, closeList) != nil {
				continue
			}

			checkNode := existNode(neighbour, openList)
			// 这个邻居结点不在 openList 中
			if checkNode == nil {
				neighbour.parent = &curNode                                 // 当前结点设置为它的父结点
				d1 := curNode.g                                             // g = 当前结点到起点的距离
				d2 := calculate_G(neighbour.coordinate, curNode.coordinate) // 该邻居结点与当前结点的距离
				neighbour.g = d1 + d2
				neighbour.h = calculate_H(neighbour.coordinate, T) // h = 该邻居节点到终点的距离
				neighbour.f = neighbour.g + neighbour.h            // f = g + h
				openList = append(openList, neighbour)             // 把它加入 open list

			} else {
				// 该结点在 openList 中
				d1 := curNode.g + calculate_G(checkNode.coordinate, curNode.coordinate)
				d2 := checkNode.g

				if d1 < d2 { // 如果经由 curNode的路径更短，则将这个邻居的父节点指向 curNode 并更新 g,f
					// 在 Go 中，不允许使用指针直接修改切片元素, 需要遍历元素的下标
					index := 0
					for i, v := range openList {
						if neighbour.coordinate == v.coordinate {
							index = i
						}
					}
					openList[index].parent = &curNode
					openList[index].g = d1
					openList[index].f = neighbour.g + neighbour.h
				}
			}
		}
		// 观察每一轮结束后 openList 和 closeList 的变化：

	}

	start := time.Now() // 计时开始

	var fNode Node
	fNode.f = 0                        // 起点的优先级为0（最高）
	fNode.coordinate = F               // 起点坐标
	openList = append(openList, fNode) // 将起点装入 openList 中
	var tNode *Node
	var path []Point
	found := false

	for {
		if found { // 找到路径
			// 从终点指针开始反推路径：

			for {
				path = append(path, tNode.coordinate)
				if tNode.parent != nil {
					tNode = tNode.parent
				} else {
					break
				}
			}
			// 反转：从终点到起点，改为从起点到终点
			for i, j := 0, len(path)-1; i < j; i, j = i+1, j-1 {
				path[i], path[j] = path[j], path[i]
			}
			break
		}

		findPath() // 开始寻路

		for _, v := range openList { // 如果终点被包含在openList中，说明找到路径了
			if v.coordinate == T {
				tNode = &v
				found = true
				break
			}
		}

		if len(openList) == 0 { // openList耗尽，表示找不到路径
			found = false
			break
		}

	}
	duration := time.Since(start) // 计时结束
	fmt.Println("Running time:", duration)

	if found {
		fmt.Println("Path finding success!")
		return path
	} else {
		fmt.Println("No path was found!")
		return nil
	}

}

// 从 list 中删除一个结点
func deleteNode(list []Node, target Node) []Node {
	var newChain []Node
	for indexToRemove, v := range list {
		if v == target {
			newChain = append(list[:indexToRemove], list[indexToRemove+1:]...) // 从 openList中 移除 target
			break
		}
	}
	return newChain
}

// 判断节点是否存在于list中
func existNode(target Node, list []Node) *Node {
	for _, element := range list {
		if element.coordinate == target.coordinate { // 用XY值来判定唯一性
			return &element
		}
	}
	return nil
}

// 计算到终点的距离（H值）
func calculate_H(p1 Point, p2 Point) int {
	const D = 10 // 距离系数
	// 采用"曼哈顿距离(Manhattan distance)" :
	dx := int(math.Abs(float64(p1.x - p2.x)))
	dy := int(math.Abs(float64(p1.y - p2.y)))
	distance := (dx + dy) * D
	/*
		// 采用"切比雪夫距离(Chebyshev distance)":
		dx := math.Abs(float64(p1.x - p2.x))
		dy := math.Abs(float64(p1.y - p2.y))
		distance := int(math.Max(float64(dx), float64(dy)) * D)
	*/
	return distance
}

// 计算到起点的距离（G值）
func calculate_G(p1 Point, p2 Point) int {
	dx := math.Abs(float64(p1.x - p2.x))
	dy := math.Abs(float64(p1.y - p2.y))
	straight := int(math.Abs(dx - dy))
	bias := int(math.Min(float64(dx), float64(dy)))
	distance := straight*10 + bias*14
	return distance
}

// 寻找list中的最小结点（使用二叉堆方法）
func findMin_Heap(tree []Node) Node {
	var n = len(tree) - 1
	// 建小根堆 (percolate_down)
	for i := (n - 1) / 2; i >= 0; i-- {
		percolate_down(tree, n, i)
	}
	return tree[0]
}

// 建堆（下滤）
func percolate_down(tree []Node, size int, parent_node int) {
	left_node := 2*parent_node + 1
	right_node := 2*parent_node + 2

	var max_node = parent_node
	if left_node <= size && tree[left_node].f < tree[parent_node].f {
		max_node = left_node
	}
	if right_node <= size && tree[right_node].f < tree[max_node].f {
		max_node = right_node
	}

	if max_node != parent_node {
		tree[parent_node], tree[max_node] = tree[max_node], tree[parent_node]
		percolate_down(tree, size, max_node)
	}
}

---

五、后记

还是那句话，本文仅作抛砖引玉之用，仅仅起个入门的作用，真正要将A星算法应用在业务程序里还需要进行更多的学习。 比如说一个1280 * 720的游戏地图，可以先缩小为128*72，然后再将其二值化再进行A星寻径效率就会高很多。