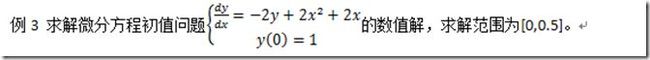【笔记】常微分方程(1)
| 主题词 | 意义 | 主题词 | 意义 |
| ode45 | 4、5阶Runge-kutta法 | ode23s | 刚性方程组二阶Rosenbrock法 |
| ode23 | 2、3阶Runge-kutta法 | ode23tb | 刚性方程组低精度算法 |
| ode113 | 多步Adams算法 | bvpinit | 边值问题预估计 |
| odeset | 解ode选项设置 | bvp4c | 边值问题解法 |
| ode23t | 适度刚性问题梯形算法 | deval | 微分方程解的求值 |
| ode15s | 刚性方程组多步Gear法 |
微分方程的相关知识
1、微分方程的概念
含有未知的函数及其某些阶的导数以及自变量本身的方程称为微分方程。如果未知函数是一元函数,称为常微分方程。如果未知函数是多元函数,称为偏微分方程。联系一些未知函数的一组微分方程称为微分方程组。微分方程中出现的未知函数的导数的最高阶数称为微分方程的阶。如果方程中未知函数及其各阶导数都是一次的,称为线性常微分方程。若各系数为常数,称之为常系数(或定常、自治、时不变)的。
2、初等积分法
有些方程可以直接通过积分求解。例如,一阶常系数线性常微分方程
y’=ay+b (a!=0)
可化为
dy/(ay+b)=dt
两边积分可得通解为:
y(t)=Cexp(at)-a^-1b
其中C为任意常数
3、常系数线性微分方程
例1 求x’’+0.2x’+3.92x=0的通解。
解: 特征方程为
λ²+0.2λ+3.92=0
>> roots([1 0.2 3.92])
ans =
-0.1000 + 1.9774i
-0.1000 - 1.9774i
求得共轭复根-0.1000 ±1.9774i,从而通解为:
x(t)=Aexp(-0.1t)cos(1.9774t)+Bexp(-0.1t)sin(1.9774t)
其中A,B为任意常数。
4、初值问题数值解
除常系数线性微分方程可用特征根法求解,少数特殊方程可用初等积分法求解外,大部分微分方程无显式解,应用中主要依靠数值解法。
考虑一阶常微分方程组初值问题
y’=f(t,y), t0<t<tf, y(t0)=y0
其中y=(y1,y2,…,ym)T,f=(f1,f2,…,fm)T,y0=(y10,y20,…,ym0)T,这里T表示转置。
所谓数值解就是寻求解y(t)在一系列离散点t0<t1<…<tn<tf上的近似值yk(k=0,1,…,n)。称hk=t(k+1)-t(k)为步长,通常取为常量h。
高阶微分方程初值问题可以化为一阶常微分方程组,已给一个n阶方程,即
解:编写如下程序:
clear
f=inline('y-2*x/y','x','y');
a=0;
b=1;
h=0.1;
n=(b-a)/h;
x=zeros(1,n+1);
y=zeros(1,n+1);
y(1)=1;
for i=1:n+1
x(i)=a+(i-1)*h;
y(i+1)=y(i)+h*f(x(i),y(i));
end
x
y=y(1:n+1)
得到结果如下:
x =
Columns 1 through 10
0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000
Column 11
1.0000
y =
Columns 1 through 10
1.0000 1.1000 1.1918 1.2774 1.3582 1.4351 1.5090 1.5803 1.6498 1.7178
Column 11
1.7848
>> % 为求精确解,输入
>> f=dsolve('Dy=y-2*x/y','y(0)=1','x')
f =
(2*x + 1)^(1/2)
>> % 在一个坐标系中画出数值解与精确解的图形:
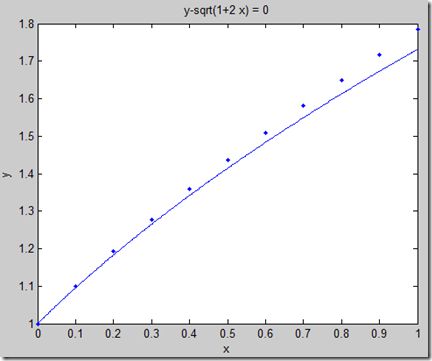
>> plot(x,y,'.b')
>> hold on
>> ezplot('y-sqrt(1+2*x)',[0,1,1,1.8])
得到图1。
图1
由图1可知,数值解和准确解比较接近,但还是有误差。
解:
>> fun=inline('-2*y+2*x^2+2*x','x','y');
>> [x,y]=ode23(fun,[0,0.5],1);
>> x';
>> y';
>> plot(x,y,'o-');
>> x'
ans =
Columns 1 through 10
0 0.0400 0.0900 0.1400 0.1900 0.2400 0.2900 0.3400 0.3900 0.4400
Columns 11 through 12
0.4900 0.5000
>> y'
ans =
Columns 1 through 10
1.0000 0.9247 0.8434 0.7754 0.7199 0.6764 0.6440 0.6222 0.6105 0.6084
Columns 11 through 12
0.6154 0.6179
图形结果见图2
图2
解微分方程的MATLAB命令
1、初值问题的求解
常微分方程求解MATLAB指令具有相同的格式,下面以最常用的ode45为例。
常用格式:[t,y]=ode45(odefun,tspan,y0)
参数说明:
odefun:用以表示f(t,y)的函数句柄或inline函数,t是标量,y是标量或向量。
tspan:如果是二维向量[t0,tf],表示自变量初值t0和终值tf;如果是高维向量[t0,t1,…,tn],则表示输出节点列向量。
y0:表示初始向量y0。
t:表示节点列向量(t0,t1,…,tn)T。
y: 表示数值解矩阵,每一列对应y的一个分量。
若无输出参数,则作出图形。
完整格式:[t,y]=ode45(odefun,tspan,y0,options,p1,p1,…)
options: 为计算参数(如精度要求)设置,默认可用空矩阵[]表示。
p1,p2,…: 为附加传递参数,这时的odefun表示f(t,y,p1,p2,…)。
注:ode45是最常用的求解微分方程的指令。它采用变步长四、五阶Runge-Kutta-Felhberg法,适合高精度问题,ode23与ode45类似,只是精度低一些。ode113是多步法,高低精度均可。这些指令对于刚性方程组不宜采用。ode23t,ode23s,ode23tb,ode15s都是求解刚性方程组的指令。
解:
(1)输入
>> dsolve('Dy=x+x*y','x')
得到含有一个任意常数的解析解:
ans =
C4*exp(x^2/2) – 1
(2)输入
>> r=dsolve('D2y=-a^2*y','y(0)=1','Dy(pi/a)=0')
r =
(1/exp(a*t*i))/2 + exp(a*t*i)/2
>> % 化为最简式
>> r=simple(r)
输出结果为:
r =
cos(a*t)
(3)输入
>> [x,y]=dsolve('Dx=y','Dy=-x')
x =
C10*cos(t) + C9*sin(t)
y =
C9*cos(t) - C10*sin(t)
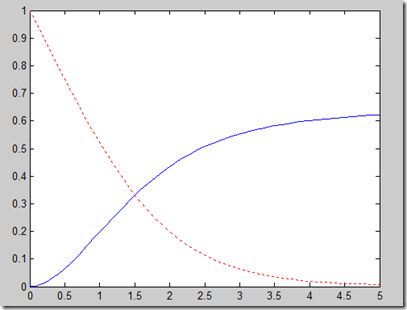
例5 解微分方程
y’=y-2t/y,y(0)=1 (0<t<4)
解:在指令窗口输入:
>> odefun=inline('y-2*t/y','t','y');
>> [t,y]=ode45(odefun,[0,4],1);
>> [t,y]
ans =
0 1.0000
0.0502 1.0490
0.1005 1.0959
0.1507 1.1408
…… ……
3.8507 2.9503
3.9005 2.9672
3.9502 2.9839
4.0000 3.0006
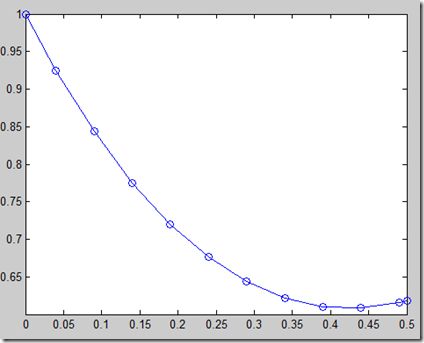
>> % 解函数图形表示,见图3
>> plot(t,y,'o-')
>> ode45(odefun,[0,4],1);
>> [t,y]=ode45(odefun,0:1:4,1);
>> [t,y]
ans =
0 1.0000
1.0000 1.7321
2.0000 2.2361
3.0000 2.6458
4.0000 3.0006
图3
事实上方程的准确解为y=sqrt(1+2t)。来比较一下几种方法的计算量和精度。下列结果中n为节点个数,反映计算量大小,e为每个节点均方误差。
>> odefun=inline('y-2*t/y','t','y');
>> [t,y]=ode45(odefun,[0,4],1);
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
45.0000 0.0002
>> [t,y]=ode23(odefun,[0,4],1);
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
13.0000 0.1905
>> [t,y]=ode113(odefun,[0,4],1);
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
18.0000 0.0097
>> [t,y]=ode23t(odefun,[0,4],1);
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
18.0000 0.0392
>> [t,y]=ode23s(odefun,[0,4],1);
Warning: Failure at t=3.925277e+000. Unable to meet integration tolerances without reducing the step size below the smallest value
allowed (1.394538e-014) at time t.
> In ode23s at 478
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
81.0000 2.5437
>> [t,y]=ode23tb(odefun,[0,4],1);
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
15.0000 0.2431
>> [t,y]=ode15s(odefun,[0,4],1);
>> n=length(t);
>> e=sqrt(sum((sqrt(1+2*t)-y).^2)/n);
>> [n,e]
ans =
22.0000 0.4551
可见,ode45精度高,但计算量比较大,ode23计算量小,但误差大。ode113适中。用刚性方程组解法解非刚性问题不太适合,特别是ode23s,计算量大且误差大。
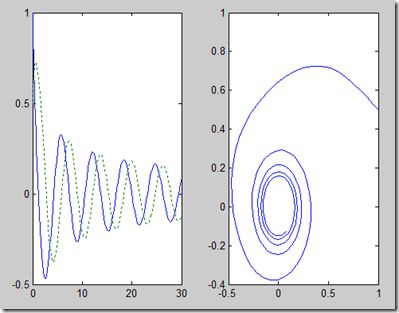
解:将变量x,y合写成向量变量x,先写M函数eg6fun.m:
% eg6fun.m
function f=eg6fun(t,x)
f(1)=-x(1)^3-x(2);
f(2)=x(1)-x(2)^3;
% 保证f为列向量
f=f(:);
再在指令窗口中执行:
[t,x]=ode45(@eg6fun,[0,30],[1,0.5]);
subplot(1,2,1);
plot(t,x(:,1),t,x(:,2),':')
subplot(1,2,2)
plot(x(:,1),x(:,2));
图4 作出了解函数图和相平面图。
图4
先些M函数eg7fun.m:
% eg7fun.m
function f=eg7fun(t,y)
f=[y(2);y(3);-3*y(1)*y(3)+2*y(2)^2-y(4);y(5);-2.1*y(1)*y(5)];
再在命令窗口中执行:
>> y0=[0 0 0.68 1 -0.5];
>> [t,y]=ode45(@eg7fun,[0,5],y0);
>> plot(t,y(:,1),t,y(:,4),':r')
图5作出了f和T的图:
图5
编写M函数文件eg8fun.m
% eg8fun.m
function f=eg8fun(t,x)
f=[x(2);7*(1-x(1)^2)*x(2)-x(1)];
再在命令窗口中输入:
>> y0=[1;0];
>> [t,x]=ode45('eg8fun',[0,40],y0);
>> y=x(:,1);
>> plot(t,y)
图6
2、边值问题解法
sinit=bvpinit(tinit,yinit):由在粗略节点tinit的预估解yiniy生成粗略解网络sinit。
sol=bvp4c(odefun,bcfun,sinit):odefun是微分方程组函数,bcfun为边值条件函数,sinit是由bvpinit得到的粗略解网络。求的边值问题解sol是一个结构,sol.x为求解节点,sol.y是y(t)的数值解。
sx=deval(sol,ti):计算由bvp4c得到的解在ti的值。
例9 求解边值问题
z’’+|z|=0, z(0)=0, z(4)=-2
解:首先改写为标准形式。令y(1)=z,y(2)=z’,则方程为
y’(1)=y(2),y’(2)=-|y(1)|
边界条件为
ya(1)=0,yb(1)+2=0
求解用下列M文件eg9fun.m。注意sol的域名。
clear;
close;
% 注意sinit的域名
sinit=bvpinit(0:4,[1;0])
odefun=inline('[y(2);-abs(y(1))]','t','y');
bcfun=inline('[ya(1),yb(1)+2]','ya','yb');
% 注意sol的域名
sol=bvp4c(odefun.bcfun,sinit)
t=linspace(0,4,101);
y=deval(sol,t);
plot(t,y(1,:),sol.x(1,:),'o',sinit.x,sinit.y(1,:),'s')
legend('解曲线','解点','粗略解')