力扣 (LeetCode) 剑指 Offer(第 2 版)刷题(java)合集-03
剑指 Offer 27. 二叉树的镜像
难度简单136
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/ \
2 7
/ \ / \
1 3 6 9
镜像输出:
4
/ \
7 2
/ \ / \
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
限制:
0 <= 节点个数 <= 1000
解法一:递归法
看起来相当舒适,就是自己想不起来,哭泣[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8ofhAHtG-1628869590627)(file:///C:\Users\LX\AppData\Local\Temp\SGPicFaceTpBq\14440\001793F3.png)]
public TreeNode mirrorTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode leftRoot = mirrorTree(root.right);
TreeNode rightRoot = mirrorTree(root.left);
root.left = leftRoot;
root.right = rightRoot;
return root;
}
方法二:辅助栈(或队列)
利用栈(或队列)遍历树的所有节点 node,并交换每个 node的左 / 右子节点。
算法流程:
特例处理: 当 root为空时,直接返回 null ;
初始化: 栈(或队列),本文用栈,并加入根节点 root。
循环交换: 当栈 stack为空时跳出;
出栈: 记为 node;
添加子节点: 将 node左和右子节点入栈;
交换: 交换 node的左 / 右子节点。
返回值: 返回根节点 root。
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root == null) return null;
Stack stack = new Stack<>() {{ add(root); }};
while(!stack.isEmpty()) {
TreeNode node = stack.pop();
if(node.left != null) stack.add(node.left);
if(node.right != null) stack.add(node.right);
TreeNode tmp = node.left;
node.left = node.right;
node.right = tmp;
}
return root;
}
}
剑指 Offer 28. 对称的二叉树
难度简单180
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ \ /
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
限制:
0 <= 节点个数 <= 1000
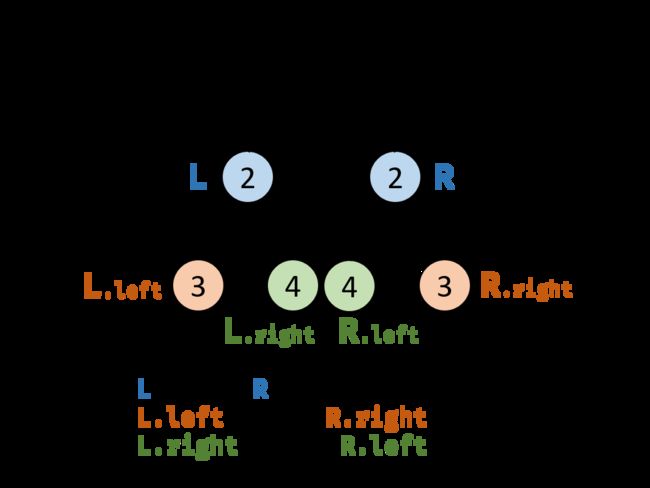
对称二叉树定义: 对于树中 任意两个对称节点 L 和 R ,一定有:
L.val = R.val:即此两对称节点值相等。
L.left.val = R.right.val:即 L 的 左子节点 和 R 的 右子节点 对称;
L.right.val = R.left.val:即 L 的 右子节点 和 R 的 左子节点 对称。
class Solution {
public boolean isSymmetric(TreeNode root) {
return root == null ? true : recur(root.left, root.right);
}
boolean recur(TreeNode L, TreeNode R) {
if(L == null && R == null) return true;
if(L == null || R == null || L.val != R.val) return false;
return recur(L.left, R.right) && recur(L.right, R.left);
}
}
剑指 Offer 30. 包含min函数的栈
难度简单133
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.
提示:
- 各函数的调用总次数不超过 20000 次
本题难点: 将 min() 函数复杂度降为O(1) ,可通过建立辅助栈实现;
数据栈 A : 栈 A 用于存储所有元素,保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。
辅助栈 B : 栈 B 中存储栈 A 中所有 非严格降序 的元素,则栈 A 中的最小元素始终对应栈 B 的栈顶元素,即 min() 函数只需返回栈 B 的栈顶元素即可。
因此,只需设法维护好 栈 B 的元素,使其保持非严格降序,即可实现 min() 函数的 O(1) 复杂度。
class MinStack {
Stack A, B;
public MinStack() {
A = new Stack<>();
B = new Stack<>();
}
public void push(int x) {
A.add(x);
if(B.empty() || B.peek() >= x)
B.add(x);
}
public void pop() {
if(A.pop().equals(B.peek()))
B.pop();
}
public int top() {
return A.peek();
}
public int min() {
return B.peek();
}
}
剑指 Offer 31. 栈的压入、弹出序列
难度中等
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
提示:
0 <= pushed.length == popped.length <= 10000 <= pushed[i], popped[i] < 1000pushed是popped的排列。
考虑借用一个辅助栈 stackstack ,模拟 压入 / 弹出操作的排列。根据是否模拟成功,即可得到结果。
入栈操作: 按照压栈序列的顺序执行。
出栈操作: 每次入栈后,循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立,将符合弹出序列顺序的栈顶元素全部弹出。
由于题目规定 栈的所有数字均不相等 ,因此在循环入栈中,每个元素出栈的位置的可能性是唯一的(若有重复数字,则具有多个可出栈的位置)。因而,在遇到 “栈顶元素 == 弹出序列的当前元素” 就应立即执行出栈。
算法流程:
初始化: 辅助栈 stack ,弹出序列的索引 i ;
遍历压栈序列: 各元素记为 num;
元素 num 入栈;
循环出栈:若 stack 的栈顶元素 == 弹出序列元素 popped[i],则执行出栈与 i++;
返回值: 若 stack 为空,则此弹出序列合法。
复杂度分析:
时间复杂度 O(N): 其中 N 为列表 pushed 的长度;每个元素最多入栈与出栈一次,即最多共 2N 次出入栈操作。
空间复杂度 O(N): 辅助栈 stack最多同时存储 N个元素。
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack stack = new Stack<>();
int i = 0;
for(int num : pushed) {
stack.push(num); // num 入栈
while(!stack.isEmpty() && stack.peek() == popped[i]) { // 循环判断与出栈
stack.pop();
i++;
}
}
return stack.isEmpty();
}
}
剑指 Offer 32 - I. 从上到下打印二叉树
难度中等
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回:
[3,9,20,15,7]
提示:
节点总数 <= 1000
class Solution {
public int[] levelOrder(TreeNode root) {
if(root == null) return new int[0];
Queue queue = new LinkedList<>(){{ add(root); }};
ArrayList ans = new ArrayList<>();
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
ans.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
int[] res = new int[ans.size()];
for(int i = 0; i < ans.size(); i++)
res[i] = ans.get(i);
return res;
}
}
剑指 Offer 32 - II. 从上到下打印二叉树 II
难度简单
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
提示:
节点总数 <= 1000
I. 按层打印: 题目要求的二叉树的 从上至下 打印(即按层打印),又称为二叉树的 广度优先搜索(BFS)。BFS 通常借助 队列 的先入先出特性来实现。
II. 每层打印到一行: 将本层全部节点打印到一行,并将下一层全部节点加入队列,以此类推,即可分为多行打印。
算法流程:
特例处理: 当根节点为空,则返回空列表 [] ;
初始化: 打印结果列表 res = [] ,包含根节点的队列 queue = [root] ;
BFS 循环: 当队列 queue 为空时跳出;
新建一个临时列表 tmp ,用于存储当前层打印结果;
当前层打印循环: 循环次数为当前层节点数(即队列 queue 长度);
出队: 队首元素出队,记为 node;
打印: 将 node.val 添加至 tmp 尾部;
添加子节点: 若 node 的左(右)子节点不为空,则将左(右)子节点加入队列 queue ;
将当前层结果 tmp 添加入 res 。
返回值: 返回打印结果列表 res 即可。
迭代:
class Solution {
public List> levelOrder(TreeNode root) {
Queue queue = new LinkedList<>();
List> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
List tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
递归:时间100%
public class Solution {
private List> ret;
public List> levelOrder(TreeNode root) {
ret = new ArrayList<>();
dfs(0, root);
return ret;
}
private void dfs(int depth, TreeNode root) {
if (root == null) {
return;
}
if (ret.size() == depth) {
ret.add(new ArrayList<>());
}
ret.get(depth).add(root.val);
dfs(depth + 1, root.left);
dfs(depth + 1, root.right);
}
}
剑指 Offer 32 - III. 从上到下打印二叉树 III
难度中等
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[20,9],
[15,7]
]
提示:
节点总数 <= 1000
方法一:层序遍历 + 双端队列
利用双端队列的两端皆可添加元素的特性,设打印列表(双端队列) tmp ,并规定:
奇数层 则添加至 tmp 尾部 ,
偶数层 则添加至 tmp 头部 。
算法流程:
特例处理: 当树的根节点为空,则直接返回空列表 [] ;
初始化: 打印结果空列表 res ,包含根节点的双端队列 deque ;
BFS 循环: 当 deque 为空时跳出;
新建列表 tmp ,用于临时存储当前层打印结果;
当前层打印循环: 循环次数为当前层节点数(即 deque 长度);
出队: 队首元素出队,记为 node;
打印: 若为奇数层,将 node.val 添加至 tmp 尾部;否则,添加至 tmp 头部;
添加子节点: 若 node 的左(右)子节点不为空,则加入 deque ;
将当前层结果 tmp 转化为 list 并添加入 res ;
返回值: 返回打印结果列表 res 即可;
class Solution {
public List> levelOrder(TreeNode root) {
Queue queue = new LinkedList<>();
List> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
LinkedList tmp = new LinkedList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
if(res.size() % 2 == 0) tmp.addLast(node.val); // 偶数层 -> 队列头部
else tmp.addFirst(node.val); // 奇数层 -> 队列尾部
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
方法二:层序遍历 + 双端队列(奇偶层逻辑分离)(自己也是写的这个,建议学习第一种,更快更短)
方法一代码简短、容易实现;但需要判断每个节点的所在层奇偶性,即冗余了 NN 次判断。
通过将奇偶层逻辑拆分,可以消除冗余的判断。
算法流程:
与方法一对比,仅 BFS 循环不同。
BFS 循环: 循环打印奇 / 偶数层,当 deque 为空时跳出;
打印奇数层: 从左向右 打印,先左后右 加入下层节点;
若 deque 为空,说明向下无偶数层,则跳出;
打印偶数层: 从右向左 打印,先右后左 加入下层节点;
复杂度分析:
时间复杂度 O(N): 同方法一。
空间复杂度 O(N): 同方法一。
class Solution {
public List> levelOrder(TreeNode root) {
Deque deque = new LinkedList<>();
List> res = new ArrayList<>();
if(root != null) deque.add(root);
while(!deque.isEmpty()) {
// 打印奇数层
List tmp = new ArrayList<>();
for(int i = deque.size(); i > 0; i--) {
// 从左向右打印
TreeNode node = deque.removeFirst();
tmp.add(node.val);
// 先左后右加入下层节点
if(node.left != null) deque.addLast(node.left);
if(node.right != null) deque.addLast(node.right);
}
res.add(tmp);
if(deque.isEmpty()) break; // 若为空则提前跳出
// 打印偶数层
tmp = new ArrayList<>();
for(int i = deque.size(); i > 0; i--) {
// 从右向左打印
TreeNode node = deque.removeLast();
tmp.add(node.val);
// 先右后左加入下层节点
if(node.right != null) deque.addFirst(node.right);
if(node.left != null) deque.addFirst(node.left);
}
res.add(tmp);
}
return res;
}
}
剑指 Offer 33. 二叉搜索树的后序遍历序列
难度中等276收藏分享切换为英文接收动态反馈
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
提示:
数组长度 <= 1000
解题思路:
后序遍历定义: [ 左子树 | 右子树 | 根节点 ] ,即遍历顺序为 “左、右、根” 。
二叉搜索树定义: 左子树中所有节点的值 << 根节点的值;右子树中所有节点的值 >> 根节点的值;其左、右子树也分别为二叉搜索树。
方法一:递归分治
根据二叉搜索树的定义,可以通过递归,判断所有子树的 正确性 (即其后序遍历是否满足二叉搜索树的定义) ,若所有子树都正确,则此序列为二叉搜索树的后序遍历。
递归解析:
终止条件: 当 i≥j ,说明此子树节点数量 \leq 1≤1 ,无需判别正确性,因此直接返回 true;
递推工作:
划分左右子树: 遍历后序遍历的 [i, j][i,j] 区间元素,寻找 第一个大于根节点 的节点,索引记为 m 。此时,可划分出左子树区间 [i,m-1][i,m−1] 、右子树区间 [m, j - 1][m,j−1] 、根节点索引 jj 。
判断是否为二叉搜索树:
左子树区间 [i, m - 1][i,m−1] 内的所有节点都应 << postorder[j] 。而第 1.划分左右子树 步骤已经保证左子树区间的正确性,因此只需要判断右子树区间即可。
右子树区间 [m, j-1][m,j−1] 内的所有节点都应 >> postorder[j] 。实现方式为遍历,当遇到 \leq postorder[j]≤postorder[j] 的节点则跳出;则可通过 p = j 判断是否为二叉搜索树。
返回值: 所有子树都需正确才可判定正确,因此使用 与逻辑符 && 连接。
p = j : 判断 此树 是否正确。
recur(i, m - 1): 判断 此树的左子树 是否正确。
recur(m, j - 1) : 判断 此树的右子树 是否正确。
class Solution {
public boolean verifyPostorder(int[] postorder) {
return recur(postorder, 0, postorder.length - 1);
}
boolean recur(int[] postorder, int i, int j) {
if(i >= j) return true;
int p = i;
while(postorder[p] < postorder[j]) p++;
int m = p;
while(postorder[p] > postorder[j]) p++;
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
}
}
剑指 Offer 34. 二叉树中和为某一值的路径
难度中等192
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树,以及目标和 target = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
返回:
[
[5,4,11,2],
[5,8,4,5]
]
提示:
节点总数 <= 10000
方法一:深度优先搜索
思路及算法
我们可以采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
代码
public class PathSum {
LinkedList> res = new LinkedList<>();
LinkedList path = new LinkedList<>();
Queue queue=new ArrayDeque<>();
public List> pathSum(TreeNode root, int target) {
recur(root, target);
return res;
}
public void recur(TreeNode root,int target){
if (root==null)
return;
path.add(root.val);
target-=root.val;
if (target==0&&root.left==null&&root.right==null)
res.add(new LinkedList<>(path));
recur(root.left,target);
recur(root.right,target);
path.removeLast();
}
}
方法二:广度优先搜索
思路及算法
我们也可以采用广度优先搜索的方式,遍历这棵树。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
为了节省空间,我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点,我们就从该节点出发不断向父节点迭代,即可还原出从根节点到当前节点的路径。
代码
class Solution {
List> ret = new LinkedList>();
Map map = new HashMap();
public List> pathSum(TreeNode root, int target) {
if (root == null) {
return ret;
}
Queue queueNode = new LinkedList();
Queue queueSum = new LinkedList();
queueNode.offer(root);
queueSum.offer(0);
while (!queueNode.isEmpty()) {
TreeNode node = queueNode.poll();
int rec = queueSum.poll() + node.val;
if (node.left == null && node.right == null) {
if (rec == target) {
getPath(node);
}
} else {
if (node.left != null) {
map.put(node.left, node);
queueNode.offer(node.left);
queueSum.offer(rec);
}
if (node.right != null) {
map.put(node.right, node);
queueNode.offer(node.right);
queueSum.offer(rec);
}
}
}
return ret;
}
public void getPath(TreeNode node) {
List temp = new LinkedList();
while (node != null) {
temp.add(node.val);
node = map.get(node);
}
Collections.reverse(temp);
ret.add(new LinkedList(temp));
}
}
复杂度分析
- 时间复杂度:O(N^2),其中 N 是树的节点数。分析思路与方法一相同。
- 空间复杂度:O(N),其中 N 是树的节点数。空间复杂度主要取决于哈希表和队列空间的开销,哈希表需要存储除根节点外的每个节点的父节点,队列中的元素个数不会超过树的节点数。
这些代码来源于力扣官网和一些大神的解答,如若侵权,本人定删。