Pytorch使用多层感知机完成MNIST手写数字识别(更新:LeNet实现Fashion-MNIST手写数字识别)
综述
数据集:MNIST手写数字数据集
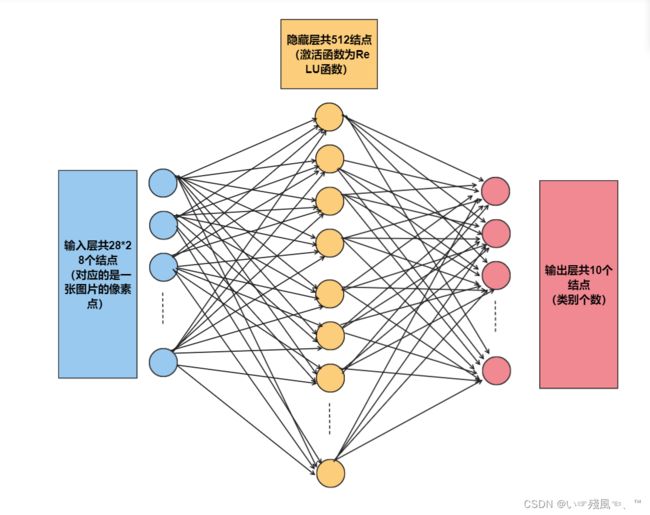
网络架构:定义了一个三层的一个感知机,其中输入层有28*28个结点,输出层有9个结点,隐藏层为512个神经元(模型中隐藏层的个数不用太多就可以)
损失函数:使用的是交叉熵损失函数
优化器:使用的是Adam优化器
数据集
对于图像的表示方法有很多,其中包括二值图像:用0表示黑色,用1表示白色;灰度图像:不仅仅有黑色和白色,还包括灰色、深灰色等,可以用256个灰度等级进行表示,取值为0到255;彩色图像:采用RGB标识;另外还有透明通道等其他表示方式等。
MNIST数据集:MNIST数据集是NIST(National Institute of Standards and Technology,美国国家标准与技术研究所)数据集的一个子集,MNIST 数据集可在 http://yann.lecun.com/exdb/mnist/ 获取,主要包括四个文件:
| 文件名 | 大小 | 内容 |
|---|---|---|
| train-images-idx3-ubyte.gz | 9,681kb | 55000张训练集,5000张验证集 |
| train-labels-idx1-ubyte.gz | 29 kb | 训练集图片对应的标签 |
| t10k-images-idx3-ubyte.gz | 1,611kb | 10000张测试集 |
| t10k-labels-idx1-ubyte.gz | 5 kb | 测试集图片对应的标签 |
在上述文件中,训练集train一共包含了 60000 张图像和标签,而测试集一共包含了 10000 张图像和标签。
idx3表示3维,ubyte表示是以字节的形式进行存储的,t10k表示10000张测试图片(test10000)。
每张图片是一个28*28像素点的0 ~ 9的灰质手写数字图片,黑底白字,图像像素值为0 ~ 255,越大该点越白。

导入数据集
# 加载 MNIST 数据集
train_dataset = datasets.MNIST(root='../data/mnist',train=True,transform=transforms.ToTensor(),download=True)
test_dataset = datasets.MNIST(root='../data/mnist',train=False,transform=transforms.ToTensor(),download=True)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True) #一批数据为100个
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,batch_size=batch_size,shuffle=False)
网络架构
定义MLP网络
# 定义 MLP 网络
class MLP(nn.Module):
# 初始化方法
# input_size 输入数据的维度
# hidden_size 隐藏层的大小
# num_classes 输出分类的数量
def __init__(self,input_size,hidden_size,num_classes):
# 调用父类的初始化方法
super(MLP,self).__init__()
# 定义第1个全连接层
self.fc1 = nn.Linear(input_size,hidden_size)
# 定义ReLu激活函数
self.relu = nn.ReLU()
# 定义第2个全连接层
self.fc2 = nn.Linear(hidden_size,hidden_size)
# 定义第3个全连接层
self.fc3 = nn.Linear(hidden_size,num_classes)
def forward(self,x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
out = self.relu(out)
out = self.fc3(out)
return out
实例化网络
# 实例化 MLP 网络
model = MLP(input_size,hidden_size,num_classes)
损失函数与优化器
损失函数采用的是交叉熵损失函数CrossEntropyLoss()。
交叉熵:它主要刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,则交叉熵定义为:
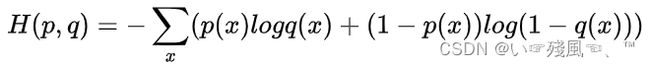
需要注意一点:Pytorch中CrossEntropyLoss()函数的主要是将softmax-log-NLLLoss合并到一块得到的结果。
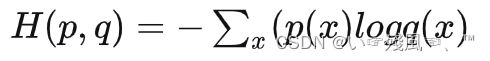
- Softmax后的数值都在0~1之间,所以 ln 之后值域是负无穷到0。
- 将Softmax之后的结果取log,将乘法改成加法减少计算量,同时保障函数的单调性 。
- NLLLoss 的结果就是把上面的输出与 Label 对应的那个值拿出来,去掉负号,再求均值。
优化器使用的是`Adam优化器。
该部分内容来自:Adam优化器(通俗理解)
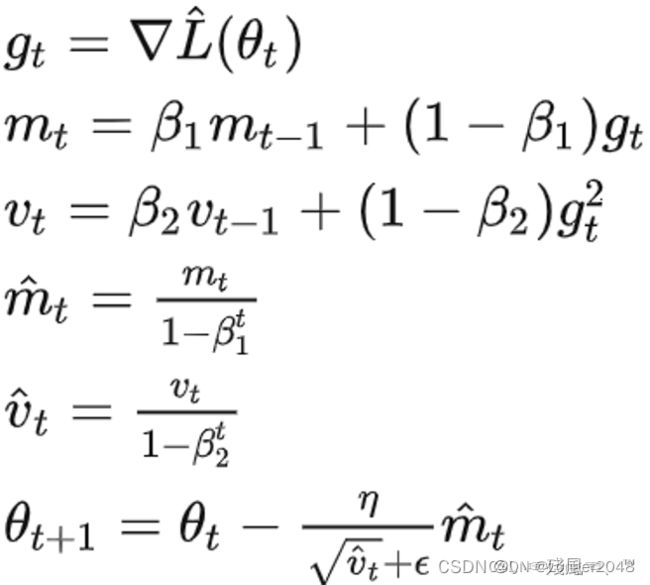
定义损失函数和优化器
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
# CrossEntropyLoss = Softmax + log + nllloss
optimizer = optim.Adam(model.parameters(),lr=learning_rate)
# optimizer = optim.SGD(model.parameters(),0.2)
训练一个MLP网络
首先根据确定的epochs的值来反复迭代训练模型,同时每次迭代都需要从train_loader中读取一batch_size个数据,并将数据转成向量(tensor),并将数据送到网络模型中。这里,在进行下一次梯度下降的时候,前一次的梯度计算结果已经没有作用了,所以需要清零。调用loss.backward方法时候,Pytorch的autograd就会自动沿着计算图反向传播,计算每一个叶子节点的梯度(如果某一个变量是由用户创建的,则它为叶子节点)。使用该方法,可以计算链式法则求导之后计算的结果值。
optimizer.step用来更新参数。
# 训练网络
# 外层for循环控制训练的次数
# 内层for循环控制从DataLoader中循环读取数据
for epoch in range(num_epochs):
for i,(images,labels) in enumerate(train_loader):
images = images.reshape(-1,28*28) #将images转换成向量
outputs = model(images) # 将数据送到网络中
loss = criterion(outputs,labels) #计算损失
optimizer.zero_grad() #首先将梯度清零
loss.backward() #反向传播
optimizer.step() #更新参数
if(i+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}],Step[{i+1}/{len(train_loader)}],Loss:{loss.item():.4f}')
完整的代码
# 导包
import torch
import torch.nn as nn #神经网络
import torch.optim as optim #定义优化器
from torchvision import datasets,transforms #数据集 transforms完成对数据的处理
# 定义超参数
input_size = 28 * 28 #输入大小
hidden_size = 512 #隐藏层大小
num_classes = 10 #输出大小(类别数)
batch_size = 100 #批大小
learning_rate = 0.001 #学习率
num_epochs = 10 #训练轮数
# 加载 MNIST 数据集
train_dataset = datasets.MNIST(root='../data/mnist',train=True,transform=transforms.ToTensor(),download=True)
test_dataset = datasets.MNIST(root='../data/mnist',train=False,transform=transforms.ToTensor(),download=True)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True) #一批数据为100个
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,batch_size=batch_size,shuffle=False)
# 定义 MLP 网络
class MLP(nn.Module):
# 初始化方法
# input_size 输入数据的维度
# hidden_size 隐藏层的大小
# num_classes 输出分类的数量
def __init__(self,input_size,hidden_size,num_classes):
# 调用父类的初始化方法
super(MLP,self).__init__()
# 定义第1个全连接层
self.fc1 = nn.Linear(input_size,hidden_size)
# 定义ReLu激活函数
self.relu = nn.ReLU()
# 定义第2个全连接层
self.fc2 = nn.Linear(hidden_size,hidden_size)
# 定义第3个全连接层
self.fc3 = nn.Linear(hidden_size,num_classes)
def forward(self,x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
out = self.relu(out)
out = self.fc3(out)
return out
# 实例化 MLP 网络
model = MLP(input_size,hidden_size,num_classes)
# 现在我们已经定义了 MLP 网络并加载了 MNIST 数据集,接下来使用 PyTorch 的自动求导功能和优化器进行训练。首先,定义损失函数和优化器;然后迭代训练数据并使用优化器更新网络参数。
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
# CrossEntropyLoss = Softmax + log + nllloss
optimizer = optim.Adam(model.parameters(),lr=learning_rate)
# optimizer = optim.SGD(model.parameters(),0.2)
# 训练网络
# 外层for循环控制训练的次数
# 内层for循环控制从DataLoader中循环读取数据
for epoch in range(num_epochs):
for i,(images,labels) in enumerate(train_loader):
images = images.reshape(-1,28*28) #将images转换成向量
outputs = model(images) # 将数据送到网络中
loss = criterion(outputs,labels) #计算损失
optimizer.zero_grad() #首先将梯度清零
loss.backward() #反向传播
optimizer.step() #更新参数
if(i+1) % 100 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}],Step[{i+1}/{len(train_loader)}],Loss:{loss.item():.4f}')
# 最后,我们可以在测试数据上评估模型的准确率:
# 测试网络
with torch.no_grad():
correct = 0
total = 0
# 从test_loader中循环读取测试数据
for images,labels in test_loader:
# 将images转换成向量
images = images.reshape(-1,28*28)
# 将数据传送到网络
outputs = model(images)
# 取出最大值对应的索引 即预测值
_,predicted = torch.max(outputs.data,1) #返回一个元组:第一个为最大值,第二个是最大值的下标
# 累加labels数量 labels为形状为(batch_size,1)的矩阵,取size(0)就是取出batch_size的大小(该批的大小)
total += labels.size(0)
# 预测值与labels值对比 获取预测正确的数量
correct += (predicted == labels).sum().item()
# 打印最终的准确率
print(f'Accuracy of the network on the 10000 test images: {100 * correct/total}%')
# 保存模型
torch.save(model,"mnist_mlp_model.pkl")
更新内容:利用LeNet做MNIST手写数字识别
为什么会突然更新,原因在于最近在看CV领域的论文和模型,无巧不成拙就看到了LeNet,就如同李沐老师说的那样,LeNet在当时算力条件有限的情况下并没有收到很大的重视,但是它带来的MNIST数据集却成了业内常用的一个公开数据集了。
定义网络
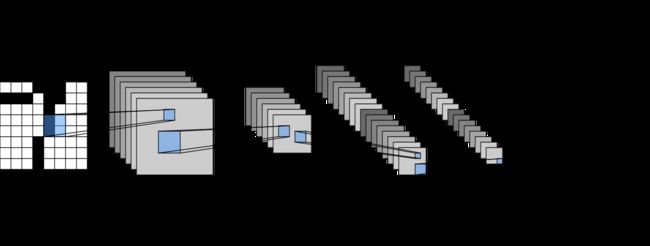
在现有的pytorch框架中使用LeNet真的是一件很容易的事情了,直接通过nn.Sequential()函数堆叠模块即可:
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),# 第一维度batch_size保持,其他维度全部拉成一个向量
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
但是torch框架有一个事情比较麻烦,就是需要自己手动算一下每一层的输入特征的情况,这里可以用两个公式表示:
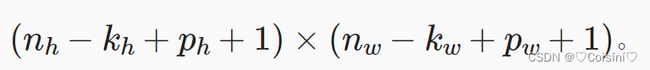
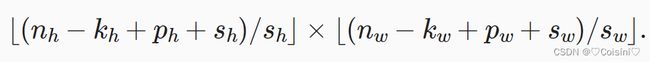
第一个公式适用于只加了padding的情况,而第二个公式既有padding也有stride的情况。下面是根据该公式计算的最终第一层线性层的输入特征大小:【这里的通道数的改变是根据论文中来的】

另外,Flatten操作是将所有的像素拉成一维,也就是形成一个条状,因为有16个通道,每个通道5*5,所以这里是400个特征值。最后不断进行降维直到形成10个类别的分类。
加载Fashion-MNIST数据集并定义超参数(批量大小)
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
直接略过!
使用GPU评估模型在Fashion-MNIST数据集上的精度
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
"""使用GPU计算模型在数据集上的精度"""
if isinstance(net, nn.Module):
net.eval() # 设置为评估模式
if not device:
device = next(iter(net.parameters())).device# 如果不告知device就将网络的device作为训练时用的device
# 正确预测的数量,总预测的数量
metric = d2l.Accumulator(2)
with torch.no_grad():
for X, y in data_iter:
if isinstance(X, list):
# BERT微调所需的(之后将介绍)
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
metric.add(d2l.accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
修改训练函数
同时为了使用GPU加速训练需要更改train_ch6()函数:
#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""用GPU训练模型(在第六章定义)"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)#输入与输出时的特征的方差 差值很小,防止模型爆炸
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr) #随机梯度下降方法--》需要learning rate
loss = nn.CrossEntropyLoss() #使用交叉熵损失函数
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,样本数
metric = d2l.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')
模型训练+LeNet评估
lr, num_epochs = 0.9, 30
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())