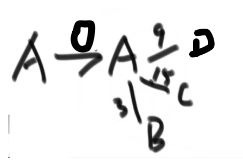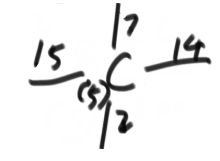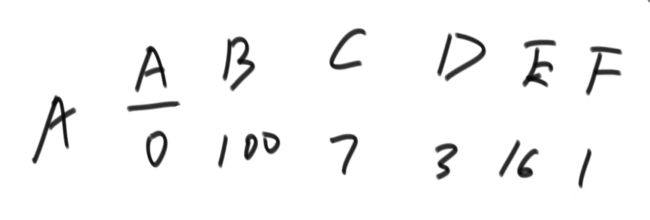图的算法

 拓扑排序算法

解析

要求：无环有向图

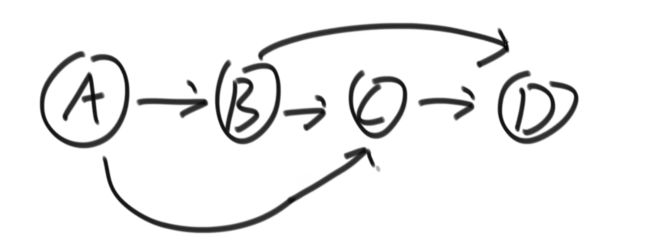
编译过程使用的是拓扑排序。A依赖BCD，在BCD三个文件编译完成才能引入A；B依赖ECD，在ECD三个文件编译完成才能引入B。拓扑排序排出整体的编译顺序E→CD→B→A

 

算法实现

找到整个图入度为0的点，打印，取消A和它的指向

再找到下一个入度为0的点，打印，取消B和它的指向

........

直到所有的节点遍历完成

package graph;

import java.util.*;

public class Sort {
    public static List topologicalSorting(Graph graph) {
        if (graph == null) {
            return null;
        }

        //HashMap,Node节点, Integer剩余的入度
        HashMap hashMap = new HashMap<>();
        Queue queue = new LinkedList<>();//记录入度为0的节点

        //记录map，找到入度为0的节点
        for (Node value : graph.nodes.values()) {
            hashMap.put(value, value.in);
            //找到入度为的节点，直接入队列
            if (value.in == 0) {
                queue.add(value);
            }
        }

        List result = new ArrayList<>();
        //将A放入result，并且取消A和它的指向
        while (!queue.isEmpty()) {
            Node node = queue.poll();
            result.add(node);
            for (Node node0 : node.nexts) {//A节点的next指向
                hashMap.put(node0, node0.in - 1);//取消A节点的指向，即下一个节点入度-1
                if (hashMap.get(node0) == 0) {//node0.in - 1 == 0
                    queue.add(node0);
                }
            }
        }

        return result;
    }
}

kruskal算法

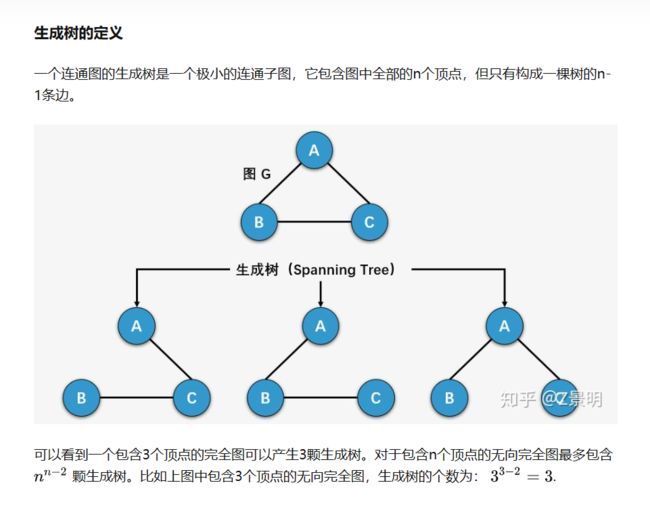
 生成最小生成树

生成树：保证连通性

最小生成树：在所有的生成树中，各个边的累加的权值是最小的

算法实现解析

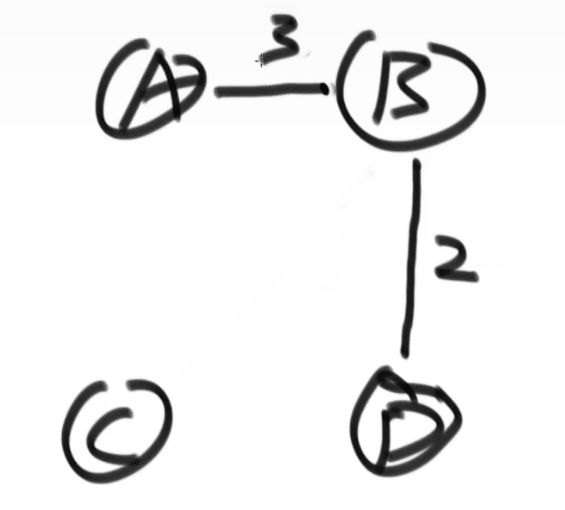
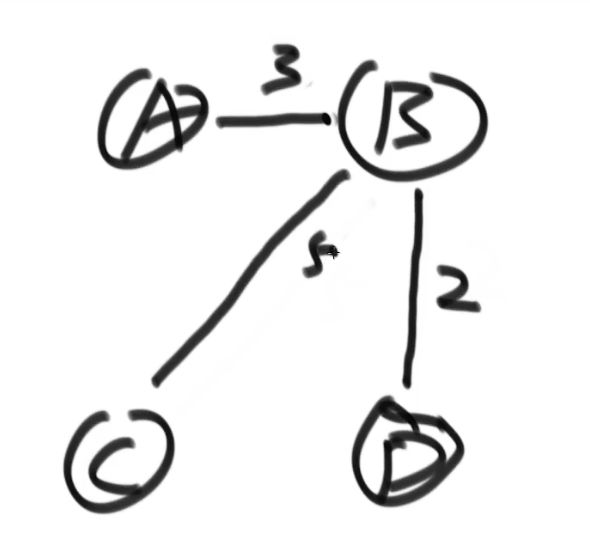
从权值最小的边开始考虑，考虑在加上这条边之后，这个图是否有形成环

没环加上，有环不要

                  

                        

如何判断是否形成环？

不使用HashSet结构，因为一开始所有的点都是存在的

令所有的点一开始各自为一个集合，根据图的边集的权值从小到大查看，查看边的from和to是否在一个集合中，如果不在，则合并两个集合；如果在，那么说明这条边加上就会形成环，跳过

实现集合的合并，查询：并查集结构

并查集结构简单版本

package graph;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;

public class SingleMergeSet {
    public static HashMap> map;

    //初始化集合，让每个节点自己一个集合
    public static void initSet(HashMap nodes) {
        for (Node node : nodes.values()) {
            List listNode = new ArrayList<>();
            listNode.add(node);//将自己添加到自己的集合
            map.put(node, listNode);
        }
    }

    //判断是否在同一个集合
    public static boolean insameSet(Node from, Node to) {
        List listFrom = map.get(from);
        List listTo = map.get(to);
        return listFrom == listTo;//比较地址值判断两个节点是否属于同一个集合
    }

    //合并集合
    public static void mergeSet(Node from, Node to) {
        List listFrom = map.get(from);
        List listTo = map.get(to);
        for (Node toNode : listTo) {
            listFrom.add(toNode);
            map.put(toNode,listFrom);
            //其实并没有改变listTo集合的地址值，只是把集合中的值全部加到listFrom集合，但是下一次取值的时候是从map集合里面取值，从一个集合里面取值的地址值相同
        }
    }
}

并查集结构可以将上述结构实现为O(n)的算法

在kruskal算法实现的时候，我们可以直接使用并查集的结构

kruskal算法

package graph;

import java.util.*;

public class Kruskal implements Comparator {

    //kruskal算法
    public static Set kruskalMST(Graph graph) {
        SingleMergeSet singleMergeSet = new SingleMergeSet();//可以替换并查集
        singleMergeSet.initSet(graph.nodes);//初始化集合、创建集合
        PriorityQueue priorityQueue = new PriorityQueue();//堆结构

        for (Edge edge : graph.edges) {
            priorityQueue.add(edge);//把边放入堆里面
        }
        
        Set result = new HashSet<>();//result返回保留哪些边
        HashMap> map = SingleMergeSet.map;

        while (!priorityQueue.isEmpty()) {
            Edge edge = (Edge) priorityQueue.poll();//堆结构按照边的权值从小到大排序，从小到大的顺序由比较器决定
            Node from = edge.from;
            Node to = edge.to;

            if (!SingleMergeSet.insameSet(from, to)) {//from和to不在同一个集合之中
                result.add(edge);//保留这条边
                SingleMergeSet.mergeSet(from, to);//合并from节点所在的集合&to节点所在的集合
            }
        }
        
        return result;
    }

    @Override
    public int compare(Edge o1, Edge o2) {//比较器
        return o1.weight - o2.weight;
    }
}

prim算法

prim算法：同样是实现最小生成树 

从点的角度出发，最终的实现和k算法是一样的 

算法实现解析

由于prim算法是把一个一个点加到集合之中，只需要使用Set结构；而kraskal算法可能需要随时检查两个“相距很远”的节点是否在一个集合之中，需要使用较为复杂的结构

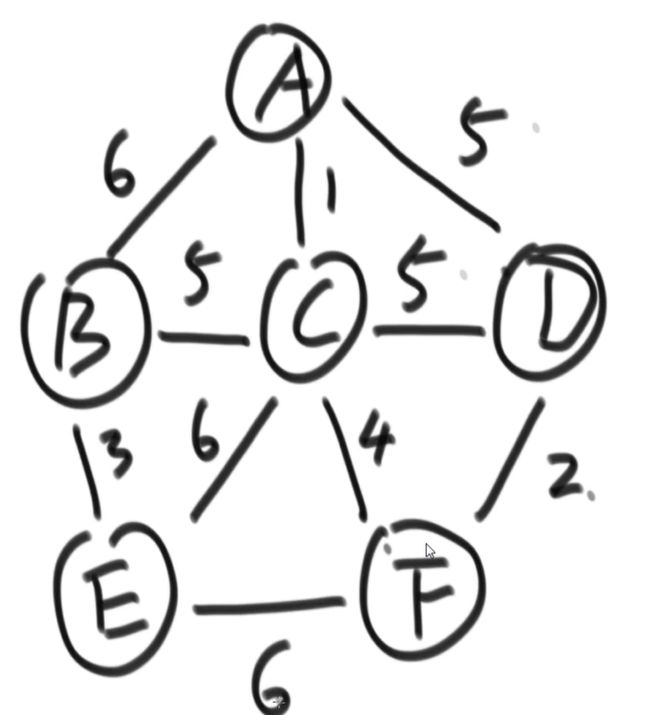
示例一：

1、可以任取一个点出发，比如从A出发，就有6，1，5三条边可以走，选择权值最小的一条边1

2、此时解锁C点，又解锁了5，5，6，4四条边，在第二轮被解锁的边中，选择权值最小的一条边4

3、F，2、6，选择2

4、D，此时它周围的边没有没被解锁的，在所有已经解锁的且没被使用的边中，挑权值最小的边

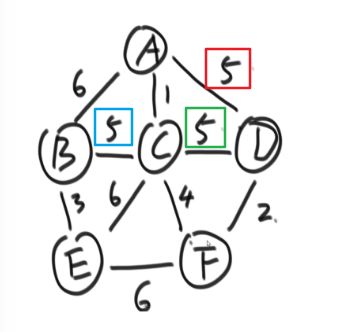
也就是6，1，5，5，5，6，4，2，6中黑色的数字，权值最小的为5。

        三个5之中，红色和绿色的5边的两个端点都已经被解锁，所以不选择；选择蓝色的5的边，解锁点B

7、B，3、6，所有已经解锁的且没被使用的边中，挑权值最小的边，选择3

8、E

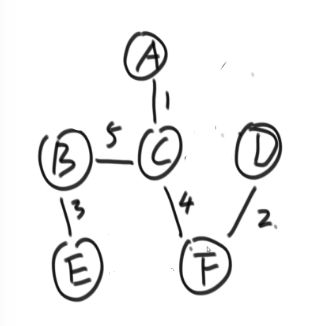
结束，所有被选择的边组成最小生成树

因为每个点都需要被连上，所以无论选择哪个点开始，选择权值最小的边就可以了

          

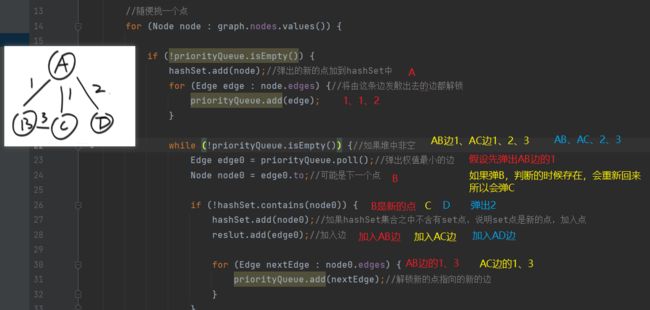
示例二：

如何判断是否是新的边？

to点是新的点，边就是新的边；to点不是新的点，边也不是新的边

如何判断是否是新的点？

解锁的点都放在set集合中

为什么使用for循环？

无向图的两边的点都既是from也是to，只要放入了，就是重复的，会被直接跳过

for循环实质上是处理森林的问题

        如果整个图是连通的，可以不使用for循环

        如果整个图非连通，那么就会在一组一组的子图内生成最小生成树

一大片的连通区域一定是一次性计算完成

for循环处理分开的集合如何生成各自的最小生成树

prim算法

package graph;

import java.util.*;

public class Prim implements Comparator {
    public static Set primMST(Graph graph) {
        HashSet hashSet = new HashSet<>();//用来存储解锁的点
        Set reslut = new HashSet<>();//result返回保留哪些边

        PriorityQueue priorityQueue = new PriorityQueue<>();//小根堆，从小到大，其中放入已经解锁的边


        //随便挑一个点
        for (Node node : graph.nodes.values()) {

            if (!priorityQueue.isEmpty()) {
                hashSet.add(node);//弹出的新的点加到hashSet中
                for (Edge edge : node.edges) {//将由这条边发散出去的边都解锁
                    priorityQueue.add(edge);
                }

                while (!priorityQueue.isEmpty()) {//如果堆中非空
                    Edge edge0 = priorityQueue.poll();//弹出权值最小的边
                    Node node0 = edge0.to;//可能是下一个点

                    if (!hashSet.contains(node0)) {
                        hashSet.add(node0);//如果hashSet集合之中不含有set点，说明set点是新的点，加入点
                        reslut.add(edge0);//加入边

                        for (Edge nextEdge : node0.edges) {
                            priorityQueue.add(nextEdge);//解锁新的点指向的新的边
                        }
                    }
                }
            }
        }
        return reslut;
    }

    @Override
    public int compare(Edge o1, Edge o2) {
        return o1.weight - o2.weight;
    }
}

Dijkstra算法

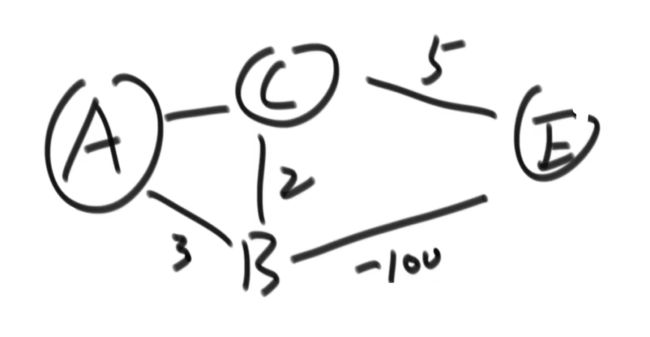
可以出现负数的边，但是不能出现整体累加和为负数的环 

Dijkstra算法：单元最短路径算法

算法实现解析

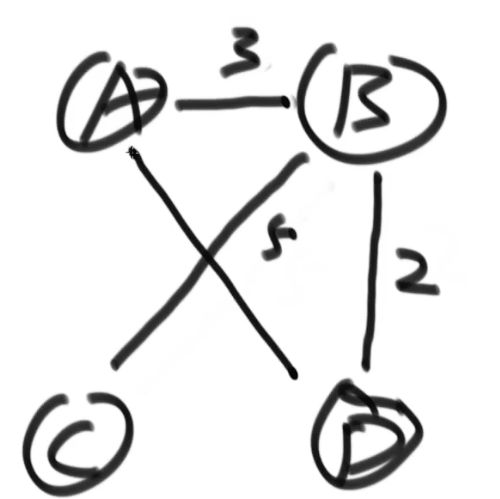
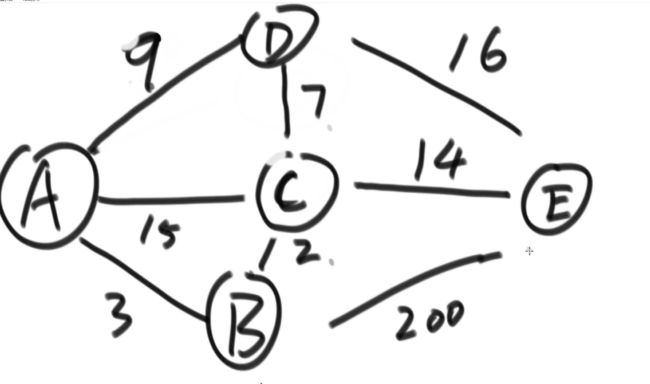
一定要规定起始点，从这个点到其后的每个点的最短路径是多少。对于不可达的点，最短距离是无穷大或是系统最大值

A - B 的最短路径为3；A - C 的最短路径为5；A - D 的最短路径为9；A - E 的最短路径为19；

      ​​​​​​​    ​​​​​​​

在每行记录中挑选最小的，由最小的这个点发散，找到到大每个点的路径长度，留较小值 

往回跳的路径一定比原来的大；比如A到B到A的路径大于A到A

	A	B	C	D	E
指定起始点A	0	∞	∞	∞	∞
	√	0+3	0+15	0+9	∞
	√	√	3+2	9	3+200
	√	√	√	9	5+14
	√	√	√	√	19
	√	√	√	√	√

为什么权值不能为负数？

出现负数的时候，很可能发生已经锁死的边发现一个更小的路径

如图出现了累加和为负数的环，那么有一种路径为A - B - E - C - B - E - C - B ......一直在CBE这个圈转下去累加和会越来越小，那么A到B的最短路径为无穷小

每一个点到其他的点的最短路径为无穷小

 

Dijkstra算法

package graph;

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;

public class Dijkstra {
    public static HashMap dijkstra(Node head) {
        //存储从head节点到其他节点的最小路径
        //key：Node节点，value：最短路径
        HashMap distanceMap = new HashMap<>();
        distanceMap.put(head, 0);

        //存储锁住的节点
        HashSet selectedNodes = new HashSet<>();


        Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);//未被锁住的节点

        while (minNode != null) {
            int distance = distanceMap.get(minNode);//当前查找出的未被锁住的最小的节点到head节点的距离

            for (Edge edge : minNode.edges) {//从节点发散的边遍历
                if (!distanceMap.containsKey(edge.to)) {
                    //第一次加的时候没有值，需要判断
                    distanceMap.put(edge.to, distance + edge.weight);
                } else {
                    //修改，比较新的distance + edge.weight路径和原来的路径，取值更小的
                    distanceMap.put(edge.to, Math.min(distance + edge.weight, distanceMap.get(edge.to)));
                }
            }
            //锁住节点
            selectedNodes.add(minNode);
            //获取下一个路径最小的节点
            minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes)
        }

        return distanceMap;
    }


    //得到没有锁住的节点中当前的路径最小的节点
    public static Node getMinDistanceAndUnselectedNode(HashMap distanceMap, HashSet selectedNodes) {
        Integer min = Integer.MAX_VALUE;//寻找当前路径最小的节点

        for (Node node0 : distanceMap.keySet()) {
            if (!selectedNodes.contains(node0)) {//节点没有被锁住
                min = Math.min(min, distanceMap.get(node0));//寻找min
            }
        }
        for (Node node0 : distanceMap.keySet()) {
            if (!selectedNodes.contains(node0) && distanceMap.get(node0) == min) {
                return node0;//找到最小的路径，返回节点
            }
        }
        return null;
    }

    public static Node getMinDistanceAndUnselectedNode1(HashMap distanceMap, HashSet selectedNodes) {
        Node minNode = null;
        int minDistance = Integer.MAX_VALUE;

        for (Map.Entry entry : distanceMap.entrySet()) {
            Node node = entry.getKey();//拿到key
            int distance = entry.getValue();//拿到value
            //节点没有被锁住 && 当前节点到head节点的路径小于找到的最小路径 -- 也就是说找到了一个更小的路径
            if (!selectedNodes.contains(node) && distance < minDistance) {
                //赋值
                minNode = node;
                minDistance = distance;
            }
        }
        return minNode;
    }

}

关于使用堆结构

遍历的方式选择最小值

用堆选择最小值：但实际不能用原始的堆结构，因为在往下走的过程中，起始点A到其他点的距离是会被突然改写的，某个较大的值可能突然变成某个较小的值，堆结构中无法变化值。如果修改每一次入堆的值，需要使用全局扫描的方式，实现算法的代价很高

如果要使用堆结构，需要手动优化堆结构，自己实现需要的堆结构