数据结构----线性表之双向链表
目录
- 前言
- 1.双向链表的介绍
- 2.相关功能接口
-
- 2.1创造头指针
- 2.2创造结点
- 2.3头部插入与尾部插入
-
- 2.3.1头部插入
- 2.3.2尾部插入
- 2.4头删和尾删
-
- 2.4.1头删
- 2.4.2尾删
- 2.4.3判空
- 2.5查找
- 2.6删除
- 2.7在pos之前插入
- 2.8销毁链表
- 2.8打印
- 3.整体代码
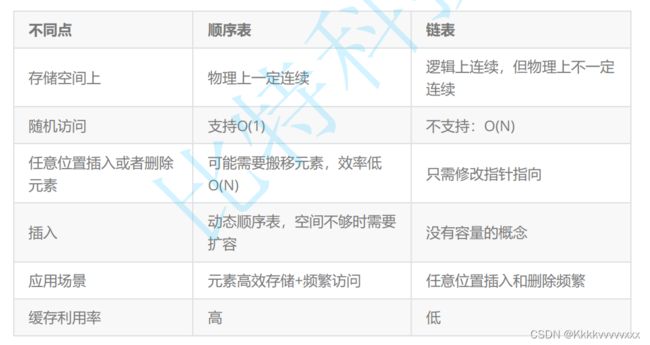
- 4.链表与顺序表的区别
- Ending
前言
本篇博客内容主要为双向链表,双向链表则很好的解决了单向链表中尾插尾删效率低下且不易操作的问题,并且单链表的插入也因双向链表从而得以优化;
1.双向链表的介绍
如图所示就是双向链表的结构,通过每个节点的首尾相互指向从而可以很轻易的实现链表中的各个操作;其结构比之单向链表复杂好多,但是其实现原理以及效率确实比单向链表高出不少!
2.相关功能接口
与之前的单链表一致,仍然需要实现其相关功能模块;首先,先对其结构进行定义:
typedef int LTDataType;
typedef struct ListNode
{
struct ListNode* next;
struct ListNode* prev;
LTDataType data;
}ListNode;
包括指向前一个结点的指针以及指向后一个结点的指针,在包含一个LTDataType类型的数据;在上篇博客中,这种方式也被提到过,因此也就不展开内容进行介绍了!
2.1创造头指针
ListNode* CreateNode()
{
ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->next = newnode;
newnode->prev = newnode;
return newnode;
}
图形结构中存在一个头指针,而这个函数就是为了创造头指针而产生的,而这个头指针并不是链表中的结点,不存储有效数据,这一点需要明确;当我们需要创造链表时,此时链表中不存在结点的,因此让头指针的next和prev统统指向头指针,当下一次进行相关函数操作时,我们可以对next和prev进行重新指向。
2.2创造结点
创造结点与单链表基本一直,在此就不在介绍了!
//创造新结点
ListNode* BuyNewNode(LTDataType x)
{
ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->next = newnode->prev = NULL;
return newnode;
}
2.3头部插入与尾部插入
2.3.1头部插入
void PushListNodeFront(ListNode* phead,LTDataType x)
{
assert(phead);
ListNode* newnode = BuyNewNode(x);
newnode->next = phead->next;
phead->next->prev = newnode;
newnode->prev = phead;
phead->next = newnode;
}
只需要将head的与新结点相关联,新结点与原来链表的首结点进行关联即可完成头插!
2.3.2尾部插入
//尾插
void PushListNodeBack(ListNode* phead, LTDataType x)
{
assert(phead);
ListNode* newnode = BuyNewNode(x);
phead->prev->next = newnode;
newnode->prev = phead->prev;
newnode->next = phead;
phead->prev = newnode;
}
头指针的前一个就是指向最后一个结点的指针,所以将新结点与原链表的最后一个结点进行连接,然后将新结点与头指针进行相连接即可!
2.4头删和尾删
2.4.1头删
void PopListNodeFront(ListNode* phead)
{
assert(phead);
assert(!ListNodeEmpty(phead));
//
ListNode* next = phead->next->next;
ListNode* cur = phead->next;
next->prev = phead;
phead->next = next;
free(cur);
}
其原理与头插非常相近,将头指针与第二个结点相关联即可,最后对第一个节点进行释放!
2.4.2尾删
void PopListNodeBack(ListNode* phead)
{
assert(phead);
assert(!ListNodeEmpty(phead));
ListNode* tail = phead->prev;
phead->prev->prev->next = phead;
phead->prev=phead->prev->prev;
free(tail);
tail = NULL;
}
phead->prev->prev->next这一句或许比较难以理解,其含义是访问倒数第二个结点的next,使其指向phead;在将phead的prev指向倒数第二个结点;
其中,phead->prev是倒数第一个节点,同理phead->prev->prev就是倒数第二个结点
2.4.3判空
在删除函数时,里边存在ListNodeEmpty这样一个函数,此函数作用就是判断链表中是否还存在结点;
而当且仅当phead->next==phead时,就意味着链表无其他元素
bool ListNodeEmpty(ListNode* phead)
{
assert(phead);
return phead == phead->next;
}
当phead == phead->next为真时返回true,否则返回false;
2.5查找
与单链表一致,查找函数主要为插入与删除做准备的;
ListNode* FindNode(ListNode* phead,LTDataType x)
{
assert(phead);
assert(!ListNodeEmpty(phead));
ListNode* cur = phead->next;
while (cur!=phead)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
2.6删除
void DeleteListNode(ListNode* pos)
{
assert(pos);
ListNode* next = pos->next;
//next是pos的后一个结点
ListNode* prev = pos->prev;
//prev是pos的前一个结点
prev->next = next;
next->prev = prev;
free(pos);
2.7在pos之前插入
void ListNodeInsert(ListNode* pos , LTDataType x)
{
assert(pos);
ListNode* newnode = BuyNewNode(x);
ListNode* prev = pos->prev;
prev->next = newnode;
newnode->prev = prev;
newnode->next = pos;
pos->prev = newnode;
}
插入的原理与尾插的原理有一些类似,可以画图进行参考,在此我就不进行赘述了!
那是否可以利用插入函数进行头插尾插当呢?
答案毋庸置疑,是可以的!
头插
void PushListNodeFront(ListNode* phead,LTDataType x)
{
assert(phead);
ListNodeInsert(phead->next, x);
}
尾插
void PushListNodeBack(ListNode* phead, LTDataType x)
{
assert(phead);
ListNodeInsert(phead, x);
}
经过在头插尾插中调用插入函数是不是逻辑很简单并且很巧妙呢!但是需要注意的是尾插时,传递的是Phead,头插传递的是phead->next;当然,具体情况是要根据当前代码是如何设计决定的!
2.8销毁链表
void DestoryListNode(ListNode* phead)
{
assert(phead);
ListNode* cur = phead->next;
while (cur!=phead)//相等即为空
{
ListNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
}
2.8打印
//打印
void PrintListNode(ListNode* phead)
{
assert(phead);
ListNode* cur = phead->next;
printf("phead<==>");
while (cur!=phead)
{
printf("%d<==>", cur->data);
cur = cur->next;
}
printf("\n");
}
3.整体代码
#define _CRT_SECURE_NO_WARNINGS
#define _CRT_SECURE_NO_WARNINGS
#include4.链表与顺序表的区别
在介绍区别之前,我想就它们二者之间的结构体定义进行罗列:
1️⃣
顺序表:
typedef int DataType;
typedef struct SeqList
{
DataType* arr;
int size;
int capacity;
}SeqList;
其中arr的本质就是一格数组,我们在使用顺序表的时候,可以对这个数组进行赋值;而为了保证数组的大小可以随着数据的增多而变大,我们在这使用了动态的方式,进行扩容;具体的相关操作,请转到这篇博客当中:顺序表的有关介绍
2️⃣
链表
typedef int SListData;
typedef struct SListNode
{
SListData data;
struct SListData* next;
}SListNode;
单链表的结构体意味着结点,通过其中的next将多个结点进行一个链接;
- 支持随机访问
- 尾插尾删的效率是相对较高的
缺点:
- 其头部中部的插入删除的效率较低
- 扩容时一定情况下会造成空间浪费
链表的优点: - 任意位置的插入删除时比较方便的,本篇博客中的双向链表就是了!
- 可以实时按需释放空间
然而,较之于两者,顺序表的最大的优点是其缓存的利用率是比较高的!
- 首先会在高速缓存中寻找数据,若数据存在(命中),即访问;
- 如数据不再高速缓存中,则需要从主存等地方拿取放置高速缓存中,在进行拿取数据!
- 而在从缓存中拿取数据时,不会一次只拿取1个字节,会根据硬件特性去拿取字节,也就是从某一内存开始拿取n个字节的数据,这个n有取决于硬件!
因此,在访问时,由于顺序表的内存地址是连续开辟的,所以命中的概率就大,内存的利用率比较高;而链表的地址不一定连续,所以缓存的利用率就比较低!
Ending
本次关于线性表的双向链表也就完成了!而在链表中,还存在一种叫做带有哨兵头的这样一种链表我并没有写出来,其结构与单向链表是一致的,唯一不一样的就是其多了一个结点;