单链表经典OJ题(二)
目录
1、链表的回文结构
2、链表分割
3、随机链表的复制
4、相交链表
5、环形链表
6、环形链表二
1、链表的回文结构
链表的回文结构_牛客题霸_牛客网 (nowcoder.com)
回文结构类似于:1->2->3->3->2->1,具体解题思路如下:
1、利用快慢指针的特性找到链表的中间结点
快慢结点的特性:如果链表有效结点个数为单数,则当快指针指向的结点为空或快指针指向的下一个结点为空时,慢指针指向该链表的中间结点。如果链表有效结点个数为双数,则当快指针指向的结点为空或快指针指向的下一个结点为空时,慢指针指向该链表的中间两个结点的后一个结点,也就是上图所示的情况
2、中间结点后的结点逆置
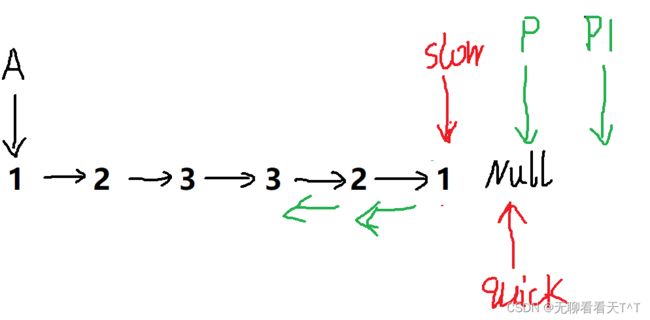
这里的可以忽视快指针quick,p1指针的作用就是为了记住p指针的下一个结点,这里的主角就是慢指针slow和p指针,先令p->next指向此时slow指向的中间结点,此时完成其中一对结点的方向逆置,接下来两个结点都向后走,先让slow指向p指针所指向的结点,然后再让p指针指向p1所指向的结点,最后p1再往后走一个结点,至此一次逆置循环结束,第二次循环与第一次循环的执行方式一样,最后结果如图二所示,第二次循环结束后p仍未指向空所以还可以进行第三次循环,当第三次循环时由于p1在第二次循环结束时已经指向了NULL,所以第三次循环令p指向p1所指向的位置时,p应该指向空,此时slow已经指向链表的最后一个结点了,最后由于p在第三次循环后变为空指针所以不会再有第四次循环
3、开始进行多种比较,主要还是比较一对儿结点中存放的有效值是否相同
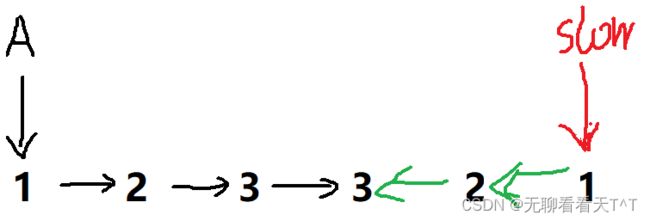
经过上述的逆置操作,此时slow指针和A指针应该已经分别指向链表的两端结点,此时首先应该保证A指针不会与slow指针重合如果重合直接返回true即可,这一步其实与刚开始时判断A->next是否为空的操作有异曲同工之妙,如果不重合则判断此时两指针所指向结点中存放的有效值是否相等,如果不相等则直接判断为非回文结构返回flase,如果相等则令两指针都向前移动一个结点,后续进行逐对儿判断链表两端结点中存放的有效值是否相同,如果直到A指针指向的结点与slow指针指向的结点相邻时仍未返回flase2,即如上图二所示的情况,此时我们应该就可以知道该链表为回文结构了,故当A->next == slow时可以判断链表为回文结构
最终代码如下:
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
//如果链表不存在,则返回值为false
if(A==NULL)
return false;
//如果链表只有一个有效结点,则返回值为true
else if(A->next==NULL)
return true;
//利用快慢指针找出中间节点
ListNode* quick = A;
ListNode* slow = A;
只要快指针及快指针的下一个结点不为空则快慢指针继续向前移动
while(quick != NULL && quick->next != NULL)
{
//快指针每次移动两个结点
quick=quick->next->next;
//慢指针每次移动一个结点
slow=slow->next;
}
//中间结点后结点的逆置
ListNode* p=slow->next;
ListNode* p1=p->next;
while(p!=NULL)
{
p->next=slow;
slow=p;
p=p1;
p1=p1->next;
}
//开始进行多种比较,主要还是比较一对儿结点中存放的有效值是否相同
while(A!=slow)
{
if((A->val)!=(slow->val))
{
return false;
}
else
{
if(A->next==slow)
{
return true;
}
A=A->next;
slow=slow->next;
}
}
return true;
}
};2、链表分割
链表分割_牛客题霸_牛客网 (nowcoder.com)
假设链表为:5->7->9->4->6->2->3,其中x=4,具体解题思路如下:
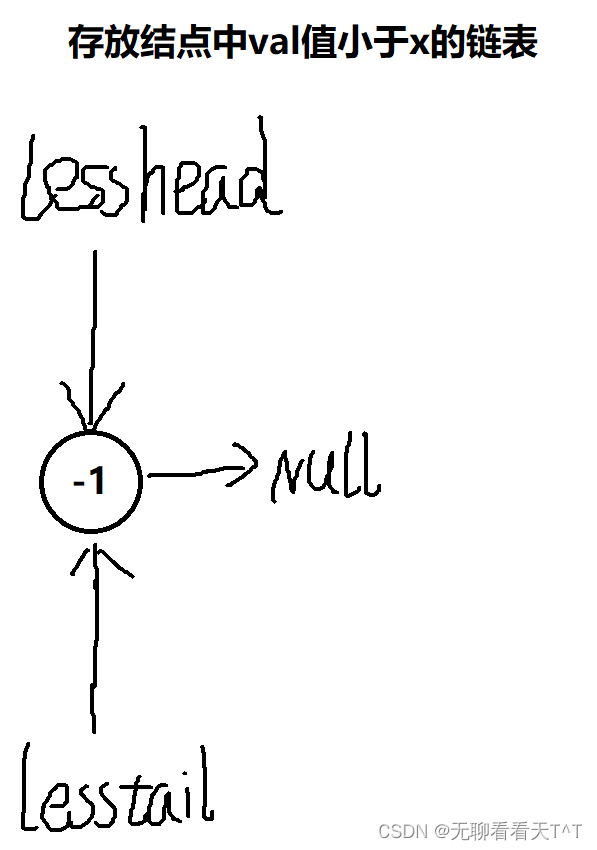
1、创建一个用于存放结点中val小于x的链表
链表有哨兵位时,对链表进行尾插就无需判断链表是否为空
先创建一个存放无效值的哨兵位结点,开始时lesshead和lesstail都指向该哨兵位的结点空间,但是lesstail后续在进行尾插时会移动,而lesshead在后续拼接链表时才会起作用
ListNode* lesshead,*lesstail;
lesshead=lesstail=(ListNode*)malloc(sizeof(ListNode));
lesshead->val = -1;
lesstail->next=NULL;
2、创建一个用于存放结点中val大于等于x的链表(图中少写了个等于)
链表有哨兵位时,对链表进行尾插就无需判断链表是否为空
先创建一个存放无效值的哨兵位结点,开始时greathead和greattail都指向该哨兵位的结点空间,但是greattail后续在进行尾插时会移动,而greathead在后续拼接链表时才会起作用
ListNode* greathead,*greattail;
greathead=greattail=(ListNode*)malloc(sizeof(ListNode));
greathead->val = -1;
greattail->next=NULL;3、遍历原链表,将原链表中的符合条件的结点分别尾插进新创建的两个链表中
while(pHead)
{
//如果原链表中结点的val值小于x,就将该结点尾插进合适的链表中,同时pHead和lesstail均指向下一个结点
if(pHead->valnext=pHead;
pHead=pHead->next;
lesstail=lesstail->next;
}
//如果原链表中结点的val值大于等于x,就将该结点尾插进合适的链表中,同时pHead和greattail均指向下一个结点
else
{
greattail->next=pHead;
pHead=pHead->next;
greattail=greattail->next;
}
}
最终结果如下:
4、拼接两个新创建的链表,并进行一些善后操作
//由于题目要求是将所有小于x的结点排在其余结点之前,所以要令lesstail->next = greathead->next
lesstail->next=greathead->next;
//为拼接后的链表创建一个新的头结点newHead
ListNode* newhead=lesshead->next;
//拼接结束后由于lessHead和greatHead这两个哨兵位已经没有用处了,所以要将为这两个哨兵位申请的内存空间释放掉
free(lesshead);
free(greathead);
//最后一定要将greattail->next置为空,否则还是会报错
greattail->next=NULL;
//应题目要求,返回重新排列后的链表的头指针newHead
return newhead;最终代码如下:
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
class Partition {
public:
ListNode* partition(ListNode* pHead, int x) {
//创建一个用于存放结点中val小于x的链表
ListNode* lesshead,*lesstail;
lesshead=lesstail=(ListNode*)malloc(sizeof(ListNode));
lesshead->val = -1;
lesstail->next=NULL;
//创建一个用于存放结点中val大于x的链表
ListNode* greathead,*greattail;
greathead=greattail=(ListNode*)malloc(sizeof(ListNode));
greathead->val = -1;
greattail->next=NULL;
//遍历原链表,将原链表中的符合条件的结点分别尾插进新创建的两个链表中
while(pHead)
{
//如果原链表中结点的val值小于x,就将该结点尾插进合适的链表中,同时pHead和lesstail均指向下一个结点
if(pHead->valnext=pHead;
pHead=pHead->next;
lesstail=lesstail->next;
}
//如果原链表中结点的val值大于x,就将该结点尾插进合适的链表中,同时pHead和greattail均指向下一个结点
else
{
greattail->next=pHead;
pHead=pHead->next;
greattail=greattail->next;
}
}
//由于题目要求是将所有小于x的结点排在其余结点之前,所以要令lesstail->next = greathead->next
lesstail->next=greathead->next;
//为拼接后的链表创建一个新的头结点newHead
ListNode* newhead=lesshead->next;
//拼接结束后由于lessHead和greatHead这两个哨兵位已经没有用处了,所以要将为这两个哨兵位申请的内存空间释放掉
free(lesshead);
free(greathead);
//最后一定要将greattail->next置为空,否则还是会报错
greattail->next=NULL;
//应题目要求,返回重新排列后的链表的头指针newHead
return newhead;
}
}; 3、随机链表的复制
138. 随机链表的复制 - 力扣(LeetCode)
具体解决思路如下:
1、利用循环插入新节点A' B' C',将原来的A->B->C的链表结点变为A->A'->B->B'->C->C':
for (struct Node* node = head; node != NULL; node = node->next->next)
{
struct Node* nodeNew = (struct Node*)malloc(sizeof(struct Node));
nodeNew->val = node->val;
nodeNew->next = node->next;
node->next = nodeNew;
}2、将上一次循环结束后位于末尾的node指针和nodeNew指针重新回到原来的位置,接下来进行A B C三个结点的random指针的拷贝,具体方式是利用三元运算符判断node->random是否为空,如果为空则新开辟的结点A'的random就指向空,如果node->random不为空则令新开辟的结点A'的random指向node指针所指向的结点中的random指针指向的结点的下一个结点即node->random->next,这是因为我们在第一次循环时已经将链表的整体顺序变为了A->A'->B->B'->C->C'的形式,为了保证深拷贝的完整性,新创建的三个结点A' B' C'中的random指针只能指向包含NULL在内的这三个新建立结点,正因如此他不能仅仅令nodeNew->random=node->random这样只是让新节点的random指针指向原来的某个结点而非新创建的三个结点,而只有令nodeNew->random = node->random->next才能做到这点
for (struct Node* node = head; node != NULL; node = node->next->next)
{
struct Node* nodeNew = node->next;
nodeNew->random = (node->random != NULL) ? node->random->next : NULL;
}3、 为深拷贝的链表创建一个新的头结点headNew,再次利用循环切断新旧链表之间的指针联系,
最后返回创建的新的头结点headNew
其实这一次的循环就是为了断开图中新旧链表相连的蓝线并将新链表结点串起来
struct Node* headNew = head->next;
for (struct Node* node = head; node != NULL; node = node->next)
{
struct Node* nodeNew = node->next;
node->next = node->next->next;
nodeNew->next = (nodeNew->next != NULL) ? nodeNew->next->next : NULL;
}
return headNew;
最终代码如下:
struct Node* copyRandomList(struct Node* head) {
if (head == NULL)
{
return NULL;
}
for (struct Node* node = head; node != NULL; node = node->next->next)
{
struct Node* nodeNew = (struct Node*)malloc(sizeof(struct Node));
nodeNew->val = node->val;
nodeNew->next = node->next;
node->next = nodeNew;
}
for (struct Node* node = head; node != NULL; node = node->next->next)
{
struct Node* nodeNew = node->next;
nodeNew->random = (node->random != NULL) ? node->random->next : NULL;
}
stru ct Node* headNew = head->next;
for (struct Node* node = head; node != NULL; node = node->next)
{
struct Node* nodeNew = node->next;
node->next = node->next->next;
nodeNew->next = (nodeNew->next != NULL) ? nodeNew->next->next : NULL;
}
return headNew;
}
4、相交链表
160. 相交链表 - 力扣(LeetCode)
我们令pA和pB走过一样的路程即:pA走过的路程是:A的路程+NULL+B的路程;pB走过的路程是:B的路程+NULL+A的路程;
如果两个链表有相交结点那么,pA和pB在走这一段路的时候一定会在某一个位置相逢即pA=pB,此时返回pA即为相交结点,如果两个链表不相交则仍返回pA此时pA==NULL(这种情况可以自己画图演示一下)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
//首先你要保证这两个链表都不为空
if (headA == NULL || headB == NULL)
{
return NULL;
}
struct ListNode *pA = headA, *pB = headB;
while (pA != pB)
{
pA = pA == NULL ? headB : pA->next;
pB = pB == NULL ? headA : pB->next;
}
return pA;
}
5、环形链表
141. 环形链表 - 力扣(LeetCode)
仍然是利用快慢指针的特性来解决这个问题,快指针的速度比慢指针的速度快,如果链表存在一个环那么快指针总会与慢指针相遇
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool hasCycle(struct ListNode* head) {
if (head == NULL || head->next == NULL)
{
return false;
}
struct ListNode* slow = head;
struct ListNode* fast = head->next;
while (slow != fast)
{
if (fast == NULL || fast->next == NULL)
{
return false;
}
slow = slow->next;
fast = fast->next->next;
}
return true;
}
6、环形链表二
142. 环形链表 II - 力扣(LeetCode)
 本题要求不仅要判断链表是否带环,还要返回该环的第一个结点的值,具体解题思路如下:
本题要求不仅要判断链表是否带环,还要返回该环的第一个结点的值,具体解题思路如下:
1、设置快慢指针,判断链表是否为空以及是否带环
struct ListNode *slow = head, *fast = head;
while (fast != NULL)
{
}
return NULL;在第一次循环时如果快指针会指向空那么证明该链表不存在,直接返回NULL,接下来fast != NULL的作用就是为了判断链表是否带环,如果在fast指针移动的过程中fast会指向NULL那么证明该链表不带环仍需返回NULL
2、如果该链表存在那么就去判断该链表是否只有一个有效结点,如果是则也返回NULL,如果不是则快慢指针向前移动
if (fast->next == NULL)
{
return NULL;
}
slow = slow->next;
fast = fast->next->next;3、如果该链表带环,那么在快慢指针移动的过程中二者一定会相遇,但是每次相遇的位置不一定
当快慢指针相遇时,令一个临时指针ptr指向链表的头结点,并令该指针也开始向前逐步移动,直到它与慢指针重合,此时返回ptr指向的结点,该结点就是进入环的第一个结点,其中蕴含的数学思想如下:
假设链表有a+b个结点,其中a个结点表示未进入环前的链表结点个数,b个结点表示环中结点的个数,假设两指针相遇时慢指针走了s步,那么快指针就走了2s步(快指针每次走两步慢指针每次走一步),而快指针必然比慢指针先进入环中,而后续快指针有会在环中赶上慢指针,所以在两者相遇时快指针一定已经走了n圈环了即n*b步,所以在相遇时f=s+nb(可以理解为:你走过的路我都走过,我为了追上你一直在原地徘徊只为了再次遇上你),而由于f=2s,所以s = nb,即慢指针走了n遍环。我们还可以知道的是从链表的第一个结点开始走a+nb步必然会到达环的第一个结点,而此时我们已经知道了慢指针走了nb步,所以慢指针只需要再走a步就可以到达环的第一个结点了,而怎么样才能保证走a步呢?答案是链表第一个结点处,所以我们令ptr指向链表的第一个结点然后令ptr和慢指针都一直向前走,直到二者相遇时证明ptr也开始进入环了,而此时ptr肯定已经走了a步,慢指针也肯定走了a步,所以此时二者相遇的位置就是入环的第一个结点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode *slow = head, *fast = head;
while (fast != NULL)
{
if (fast->next == NULL)
{
return NULL;
}
slow = slow->next;
fast = fast->next->next;
if (fast == slow)
{
struct ListNode* ptr = head;
while (ptr != slow)
{
ptr = ptr->next;
slow = slow->next;
}
return ptr;
}
}
return NULL;
}
~over~