Leetcode刷题详解——黄金矿工

1. 题目链接：1219. 黄金矿工

2. 题目描述：

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

• 每当矿工进入一个单元，就会收集该单元格中的所有黄金。
• 矿工每次可以从当前位置向上下左右四个方向走。
• 每个单元格只能被开采（进入）一次。
• 不得开采（进入）黄金数目为 0 的单元格。
• 矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

示例 1：

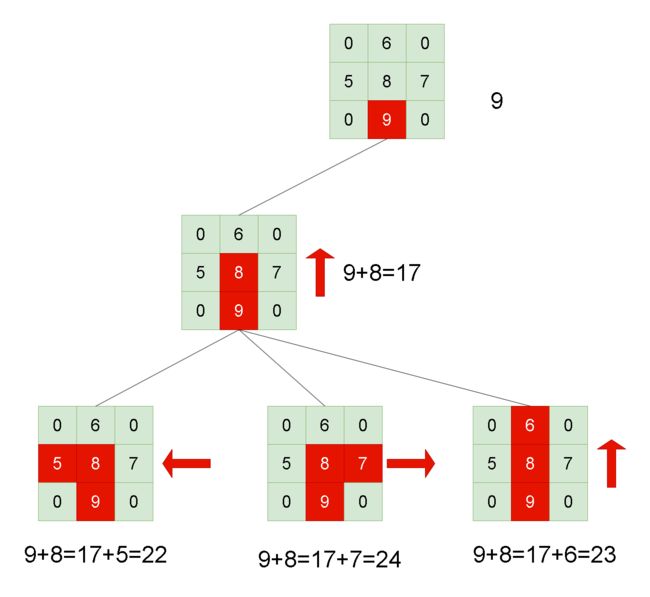
输入：grid = [[0,6,0],[5,8,7],[0,9,0]]
输出：24
解释：
[[0,6,0],
 [5,8,7],
 [0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。

示例 2：

输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28
解释：
[[1,0,7],
 [2,0,6],
 [3,4,5],
 [0,3,0],
 [9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。

提示：

• 1 <= grid.length, grid[i].length <= 15
• 0 <= grid[i][j] <= 100
• 最多 25 个单元格中有黄金。

3. 解法：

3.1 算法思路：

枚举矩阵中所有的位置当成起点，来一次深度优先遍历，统计出所有情况下能收集的黄金数的最大值即可

1. 初始化访问标记数组 vis，用于记录某个位置是否已经访问过。
2. 初始化四个方向的横坐标偏移量 dx 和纵坐标偏移量 dy。
3. 获取地图的行数 m 和列数 n。
4. 遍历地图的每一行和每一行的每个位置。
5. 如果当前位置有金币（即 g[i][j] 不为0），则进行以下操作：
   • 将当前位置标记为已访问（vis[i][j] = true）。
   • 调用深度优先搜索函数 dfs，从当前位置开始进行搜索。
   • 回溯时取消当前位置的标记（vis[i][j] = false）。
6. 在深度优先搜索函数 dfs 中，执行以下操作：
   • 更新最大金币数量 ret，将其设置为当前路径中的金币数量与 ret 之间的较大值。
   • 遍历四个方向（上、下、左、右）。
   • 计算下一个位置的坐标 x 和 y。
   • 如果下一个位置在地图内且未被访问过且有金币（即 g[x][y] 不为0），则进行以下操作：
     • 将下一个位置标记为已访问（vis[x][y] = true）。
     • 继续从下一个位置开始进行深度优先搜索，并将当前路径中的金币数量加上下一个位置的金币数量作为新的路径。
     • 回溯时取消下一个位置的标记（vis[x][y] = false）。
7. 返回最大金币数量 ret。

通过以上步骤，该算法能够找到二维网格中的最大金币数量。

3.2 C++算法代码：

class Solution {
    bool vis[16][16]; // 访问标记数组，用于记录某个位置是否已经访问过
    int dx[4]={0,0,1,-1}; // 四个方向的横坐标偏移量
    int dy[4]={1,-1,0,0}; // 四个方向的纵坐标偏移量
    int m,n; // 地图的行数和列数
    int ret; // 记录最大金币数量

public:
    int getMaximumGold(vector>& g) // 获取最大金币数量的函数
    {
        m=g.size(),n=g[0].size(); // 初始化地图的行数和列数
        for(int i=0;i>&g,int i,int j,int path) // 深度优先搜索函数
    {
        ret=max(ret,path); // 更新最大金币数量
        for(int k=0;k<4;k++) // 遍历四个方向
        {
            int x=i+dx[k],y=j+dy[k]; // 计算下一个位置的坐标
            if(x>=0&&x=0&&y