C++实现红黑树 && 模拟实现set,map
文章目录
- 前言
- insert
- erase
- iterator
- 红黑树简单实现
- 检验红黑树的性质
- set
- map
前言
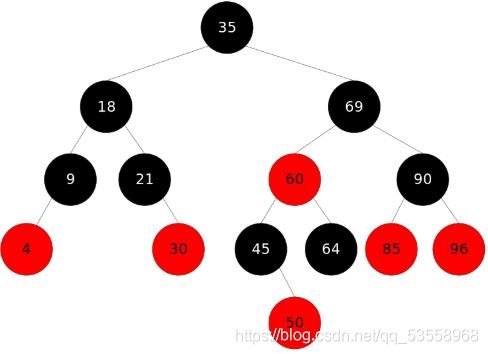
红黑树是一棵平衡二叉搜索树,它的“平衡”虽不及AVLTree,但是它的效率跟AVLTree差不多。而STL中的map和set底层就是封装了一棵红黑树。红黑树是一棵很棒的树,想要维持它这种优美的形态,自然需要付出努力,这与我们人也一样。红黑树的性质是老生常谈,但也是红黑树的根基:
- 所有节点带有颜色,要么是黑色,要么是红色。这也是红黑树名字的由来。
- 根节点是黑色。
- 每条路径上有相同数目的黑节点。
- 如果一个节点是红色,那么它的孩子一定是黑色。(我们认为叶子节点拥有两个黑色节点的孩子null。)
性质4是在说明没有连续的红节点,这几条性质加在一起能够保证红黑树的平衡——最长路径不超过最短路径的二倍。最短路径就是全黑路径,最长路径就是红黑相间的路径,这正好是二倍。
insert
考虑我们新增一个节点,那么这个节点有一个颜色,我们是给红色还是黑色好一些呢?如果我们给黑色,那么就有可能违反规则3,如果我们给红色,那么就可能违反规则4。想象一下,违反规则3的可怕后果,你需要对所有的路径进行调整,那我干脆使用AVLTree算了(笑),所以我们选择新增节点是红色的。接下来为了便于说明我把新增节点叫做cur,新增节点的父节点叫做parent,新增节点的祖父节点叫做pParent,新增节点的叔叔节点即父节点的兄弟节点叫做uncle。
如果parent节点不存在,那么cur是红色的,为了满足条件2,我们需要将cur变成黑色的。如果parent存在且为黑色,那么我们根本不需要做多余的operation,因为这样仍然符合红黑树。所以最终的问题都落到了parent节点是红色的。
情况1: 因为parent节点是红色的,所以pParent节点一定存在且为黑,否则就违反规则2。如果uncle存在且为红色,因为cur和parent是连续的红节点,所以我们将parent变成黑色,但是这样parent这条路径上就多出一个黑色节点,所以将pParent变红,最后将uncle变黑,正好符合红黑树的特性。
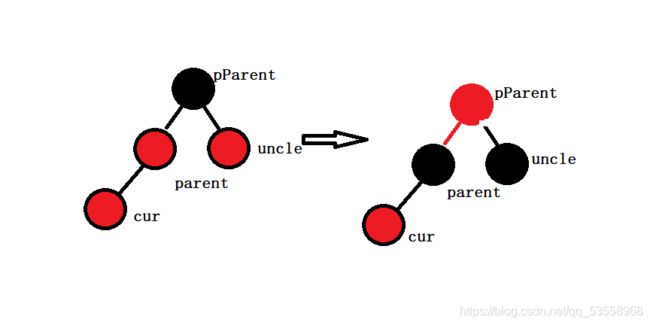
因为原来的树是红黑树,这样做保证的每条路径的黑色节点是不变的,而且没有连续的红节点。但是问题也出来了:如果pParent是根节点,那么我们需要将根节点重新变成黑色。如果pParent不是根节点,也就是说pParent也存在父亲节点,这个父亲节点一旦是黑色的,万事大吉,停止更新。一旦是红色的,我们就仍需要再次进行调整。
情况2:uncle不存在。这时候我们发现仅仅依靠变色不足以达到目的,这时候根据cur处于parent的左边还是右边,通过旋转+变色我们来搞定这种情况。
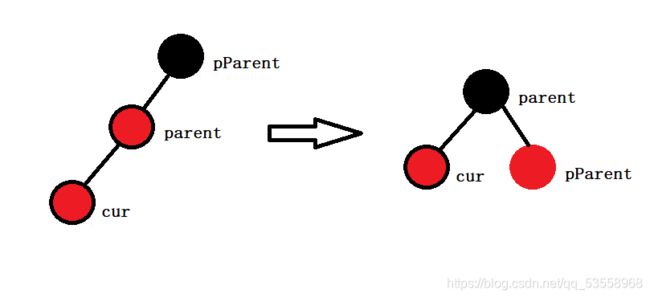
如果cur在parent的左侧,那么对pParent进行一次右单旋,然后再将parent变成黑色,pParent变成红色即可。此时parent是黑色,无论parent是否有父节点,都无需再次向上调整,调整结束。
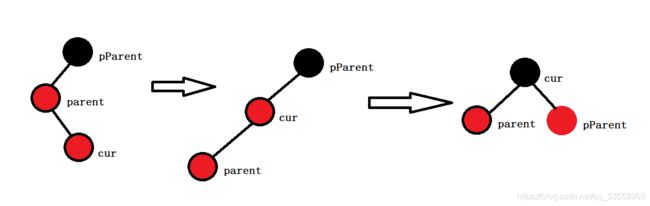
如果cur在parent的右侧,那么对parent进行一次左单旋,然后实际上就退化成了上面的那种情况,只需右单旋+变色处理即可,但是cur和parent要进行一次swap。
情况3:uncle有没有可能是黑色的呢?如果cur是新增节点的情况下,uncle是不可能为黑色的。不然cur和parent都是红色,uncle是黑色,那么uncle这条线就多一个黑色节点,违反规则3.但是有没有这样一种情况,cur不是新增节点,是通过第一种情况变成的呢?完全有可能,此时我们的做法同uncle不存在是一样的,

下面的小矩形表示若干个节点,此时我们同样的对pParent进行一次右单旋,然后将pParent变成红色,将parent变成黑色即可。cur在parent右边的做法同上面相同,不做过多讲解。
实际上,上面的讨论都是parent在pParent的左边,当parent在pParent右边时,情况完全相同。
erase
首先按照二叉搜索树的erase方法进行erase,
- 如果要删除的节点是叶子节点,那么直接干掉。
- 如果要删除的节点有一个孩子,那么干掉这个节点,让它的孩子替代它。
- 如果要删除的节点有两个孩子,那么将它右子树的最小节点RightMin的value拷贝过来,然后再删除RightMin。当然了,左子树的最大节点也是可以的。此时删除RightMin节点的方法退化成1或者2。
- 删除完毕后,如果不满足红黑树的性质,那么通过变色+旋转来调整即可。
接下来就是过山车最惊险的地方了,我们来说一说调整的情况。不妨假设被删除的节点cur是父节点parent的左孩子。
情况1:删除的是红色节点,那么万事大吉,因为删除红色节点根本不会影响红黑树的性质,直接结束。
情况2:删除的是黑色节点。由上面的删除方法,我们知道被删除的节点最多有一个孩子。下面我们对被删除节点cur的孩子进行分类。如果 cur有一个孩子,那么这个孩子的颜色一定是红色,不然就会导致另外一条没有孩子的路径少一个黑色节点。那么就好办了,我们直接把这个孩子的颜色变成黑色即可。
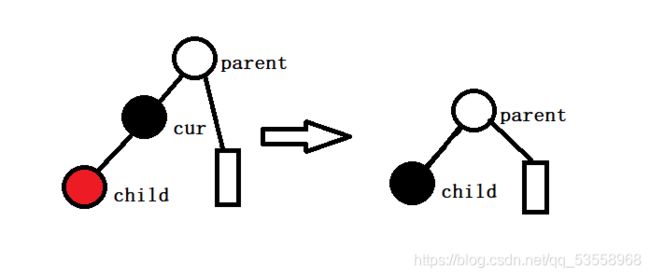
矩形代表若干节点。
如果 cur没有孩子,那么cur的父节点parent的左子树就少了一颗黑色节点,但左子树已经没有节点了,我们需要打它右子树的主意。在插入的时候,最重要的节点是uncle,同样的,删除的时候最重要的节点是brother节点,即cur的兄弟节点。
情况3:如果兄弟节点是黑色的,那么brother就可能有红色的孩子节点,也有可能没有。如果有孩子节点,我们就通过旋转将孩子节点转到左子树,然后将它的颜色变黑即可。如果兄弟节点的右孩子是红色的,那么
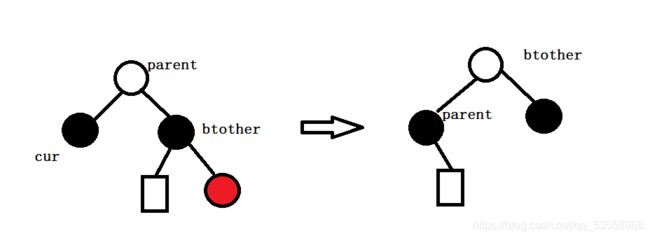
空心的圆圈表示颜色随意,矩形表示可能有节点,可能没有节点。我们的做法是对parent进行一次左单旋,然后交换brother和parent的颜色,再将brother的右孩子变成黑色。
情况4:如果brother的右孩子不存在,左孩子为红色,
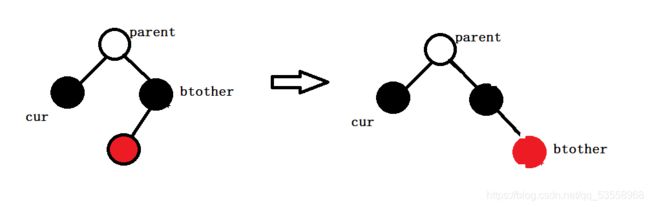
那么我们对brother进行一次右单旋,再交换brother和它左孩子的颜色,此时情况4就变成了情况3,按照情况3的方法处理即可。
情况5:brother没有孩子,那么右子树也没有多余的节点让我们去借,我们只好去看父节点。
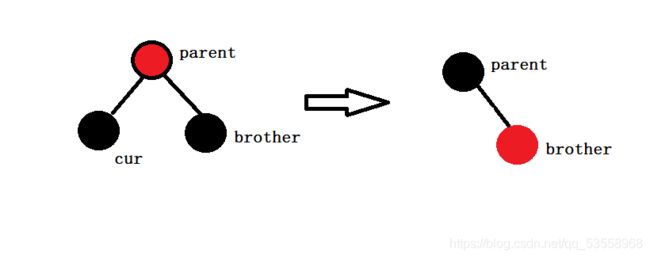
如果父节点是红色节点,那么直接交换parent和brother节点的颜色。

如果父节点是黑色节点,那么我们将brother变成红色,此时brother这条路径上的黑色节点数和cur路径上的相同,我们继续迭代向上处理,此时就变成了上面的几种情况。
情况6:如果brother是红色节点:这种情况也非常简单,既然brother是红色节点,那么它一定有两个黑色的孩子,且parent的颜色是黑色。
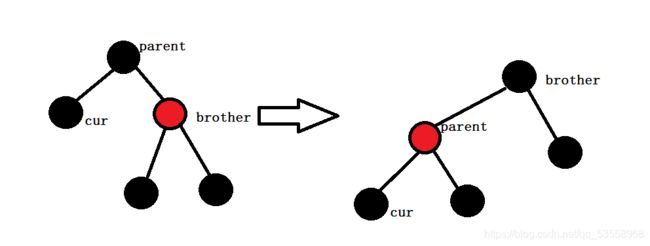
我们对parent进行一次左单旋,然后交换parent和brother的颜色,此时cur的兄弟是黑色的,就转换成了上面的几种情况。
iterator
iterator其实就是封装了一个红黑树的节点而已,其中==和!=都较简单,这里主要讲解一下++,至于–的操作,与++大抵相同,我提供了我的代码,但不做具体讲解。
iterator的operator++ :二叉搜索树的++和–采用的是中序遍历的顺序。如果当前节点右子树非空,那么++后的下一个节点就是右子树的最小节点,如果右子树为空,那么++后的节点就是当前节点的祖先,不断迭代,知道当前节点在该祖先节点的左子树上,或者遇到nullptr停止,此时也是找到了++后的节点。
template<typename Value, typename Ref, typename Ptr>
struct __rbtree_iterator { //红黑树的迭代器
using Self = __rbtree_iterator<Value, Ref, Ptr>;
using node = __rbtree_node<Value>;
// 5个 iterator_traits,使用using替代typedef,且等号对齐,这是VS源码的写法
using value_type = Value;
using defference_type = ptrdiff_t;
using iterator_catagory = bidirectional_iterator_tag;
using reference = Ref;
using pointer = Ptr;
// 迭代器的成员变量,封装树的节点
node* _node;
explicit __rbtree_iterator(node* node) :_node(node) {}
reference operator*() { return _node->_value; }
pointer operator->() { return &operator*(); }
Self& operator++() { //按照中序遍历的方式++
if (_node->_right) { //如果node右子树非空
node* minLeft = _node->_right;
while (minLeft->_left) {
minLeft = minLeft->_left;
}
_node = minLeft;
}
else { //node自己就是最右边的节点
node* parent = _node->_parent;
while (parent && _node == parent->_right) {
_node = parent;
parent = _node->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--() {
if (_node->_left) {
node* maxRight = _node->_left;
while (maxRight->_right) {
maxRight = maxRight->_right;
}
_node = maxRight;
}
else {
node* parent = _node->_parent;
while (parent && _node == parent->_left) {
_node = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
bool operator==(const Self& iter) { return _node == iter._node; }
bool operator!=(const Self& iter) { return !(*this == iter); }
};
接下来就是代码实现,讲解都放在注释中,其中的erase我没有测试所有的情况,有可能会出现bug,如果希望讨论或者是错误,欢迎私信我或者评论留言。还有部分如find之类的简单函数,不再实现。
红黑树简单实现
enum color{RED, BLACK};
namespace zzh {
template<typename Value>
struct __rbtree_node { //红黑树的节点,GCC库中是双层继承结构,太过复杂,我没有使用
using Self = __rbtree_node<Value>;
Self* _left;
Self* _right;
Self* _parent;
Value _value;
color _color;
explicit __rbtree_node(const Value& value)
:_left(nullptr), _right(nullptr), _parent(nullptr)
, _value(value), _color(RED) {}
};
// rbtree 默认传greater
template<typename Key, typename Value, typename KeyOfValue, typename Compare>
class rbtree {
public:
using node = __rbtree_node<Value>;
using iterator = __rbtree_iterator<Value, Value&, Value*>;
using const_iterator = __rbtree_iterator<Value, const Value&, const Value*>;
using tree = rbtree<Key, Value, KeyOfValue, Compare>;
// 还有一大堆的重命名,这是为了stl的consistence,在此我简化,不做重定义
rbtree() :_root(nullptr) {}
// 禁用copy和assign
rbtree(const tree&) = delete;
tree& operator=(const tree&) = delete;
// 析构函数
~rbtree() { _destructor(_root); }
// begin && end
iterator begin() {
if (_root == nullptr)
return iterator(nullptr);
node* cur = _root;
while (cur->_left) {
cur = cur->_left;
}
return iterator(cur);
}
const_iterator begin() const{
if (_root == nullptr)
return const_iterator(nullptr);
node* cur = _root;
while (cur->_left) {
cur = cur->_left;
}
return const_iterator(cur);
}
iterator end() { return iterator(nullptr); }
const_iterator end() const{ return end(); }
pair<iterator, bool> insert(const Value& value) {
if (_root == nullptr) {
_root = new node(value);
_root->_color = BLACK;
return make_pair(iterator(_root), true);
}
node* cur = _root;
node* parent = nullptr;
KeyOfValue kofv;
// key值大往右走
//if (kofv(value) > kofv(cur->_value)) {
while (cur) {
if (_compare(kofv(value), kofv(cur->_value))) {
parent = cur;
cur = cur->_right;
}
else if (kofv(value) == kofv(cur->_value)) {
return make_pair(iterator(cur), false);
}
else {
parent = cur;
cur = cur->_left;
}
}
// 已经找到插入位置
cur = new node(value);
if (_compare(kofv(value), kofv(parent->_value))) {
parent->_right = cur;
cur->_parent = parent;
}
else {
parent->_left = cur;
cur->_parent = parent;
}
node* InsertNode = cur;
// 插入完毕,开始调整
//我们默认插入红色节点,如果它的parent是黑色的,那么不需要调整
//如果它的parent是红色的,我们需要变色+旋转
while (parent) {
if (parent->_color == BLACK) { //如果parent是黑色的,那么插入完毕
return make_pair(iterator(cur), true);
}
//父节点是红色的
else {
node* pParent = parent->_parent;
if (pParent->_left == parent) {
node* uncle = pParent->_right;
if (uncle && uncle->_color == RED) { //uncle存在且为红色
pParent->_color = RED;
parent->_color = uncle->_color = BLACK;
cur = pParent;
parent = pParent->_parent;
}
else {
if (cur == parent->_right) { //如果cur是parent的右孩子,则转化成cur是parent的左孩子处理
rotateL(parent);
swap(cur, parent);
}
rotateR(pParent);
parent->_color = BLACK;
pParent->_color = RED;
if (parent->_parent == nullptr) { //更新根节点
_root = parent;
}
return make_pair(iterator(InsertNode), true); //这种情况下,更新完成代表插入结束
} //uncle不存在或者为黑色
} //parent是pParent的左孩子
else {
node* uncle = pParent->_left;
if (uncle && uncle->_color == RED) { //如果uncle存在且为红色
pParent->_color = RED;
uncle->_color = parent->_color = BLACK;
cur = pParent;
parent = cur->_parent;
}
else {
if (cur == parent->_left) {
rotateR(parent);
swap(cur, parent);
}
rotateL(pParent);
parent->_color = BLACK;
pParent->_color = RED;
if (parent->_parent == nullptr) { //更新根节点
_root = parent;
}
return make_pair(iterator(InsertNode), true);
}
} //parent是pParent的右孩子
}
}
_root->_color = BLACK;
return make_pair(iterator(InsertNode), true);
}
void erase(const Key& key) {
if (_root == nullptr)
return;
KeyOfValue kofv;
node* cur = _root;
node* parent = nullptr;
position pos = LEFT; //用来标记删除的节点是父节点的左孩子还是右孩子
bool flag = false;
color delete_node_color = RED;
while (cur) {
if (_compare(kofv(cur->_value), key)) { //key值比cur小,继续往左子树找
parent = cur;
cur = cur->_left;
}
else if (kofv(cur->_value) == key) {
flag = true;
//找到了,开始删除
//如果cur的左子树为空,将parent与cur->_right链接
if (cur->_left == nullptr) {
if (cur == _root) { //cur是根节点
_root = cur->_right;
_root->_parent = nullptr;
}
if (cur == parent->_left) { //cur是父节点的左孩子
parent->_left = cur->_right;
if(cur->_right)
cur->_right->_parent = parent;
pos = LEFT;
}
else { //cur是父节点的右孩子
parent->_right = cur->_right;
if(cur->_right)
cur->_right->_parent = parent;
pos = RIGHT;
}
delete_node_color = cur->_color;
delete cur;
break;
}
else if (cur->_right == nullptr) {
if (cur == _root) {
_root = cur->_left;
_root->_parent = nullptr;
}
if (cur == parent->_left) { //cur是父节点的左孩子
parent->_left = cur->_left;
if(cur->_left)
cur->_left->_parent = parent;
pos = LEFT;
}
else { //cur是父节点的右孩子
parent->_right = cur->_left;
if(cur->_left)
cur->_left->_parent = parent;
pos = RIGHT;
}
delete_node_color = cur->_color;
delete cur;
break;
}//cur的左子树非空,右子树为空
else { //左右子树都非空
node* RightMin = cur->_right;
node* RightMinParent = cur;
while (RightMin->_left) {
RightMinParent = RightMin;
RightMin = RightMin->_left;
}
cur->_value = RightMin->_value;
if (RightMin == RightMinParent->_left) {
RightMinParent->_left = RightMin->_right;
RightMin->_right->_parent = RightMinParent;
pos = LEFT;
}
else {
RightMinParent->_right = RightMin->_right;
RightMin->_right->_parent = RightMinParent;
pos = RIGHT;
}
delete_node_color = RightMin->_color;
delete RightMin;
parent = RightMinParent;
break;
}
}//找到了,开始删除
else {
parent = cur;
cur = cur->_right;
}
}
if (flag == false) //没找到要删除的数据,返回。
return;
while (parent) {
//删除完毕,开始调整红黑树
if (delete_node_color == RED) { //如果删除的是红节点,直接返回
return;
}
else { //删除的是黑色节点
//删除的是根节点
if (parent == nullptr) {
_root->_color = BLACK;
return;
}
//cur是parent的左孩子
if (pos == LEFT) {
if (parent->_left) { //如果cur有孩子,那么只能是一个红色的孩子,将它变成黑色
parent->_left->_color = BLACK;
return;
}
else { //cur没有孩子
node* brother = parent->_right;
if (brother->_color == RED) { //如果brother的颜色为红色,转换成brother是黑色的情况
rotateL(parent);
parent->_color = RED;
brother->_color = BLACK;
brother = parent->_right; //调整brother
}
//现在brother的颜色是黑色
if (brother->_left && !brother->_right) { //如果brother左孩子存在且右孩子不存在
rotateR(brother);
swap(brother->_color, brother->_right->_color);
brother = parent->_right; //调整brother
}
if (brother->_right) { //brother右孩子存在
rotateL(parent);
swap(parent->_color, brother->_color);
brother->_right->_color = BLACK;
return;
}
if (!brother->_left && !brother->_right) { //brother没有孩子
if (parent->_color == RED) { //父节点为红色
swap(parent->_color, brother->_color);
return;
}
else {
brother->_color = RED;
brother = parent;
parent = parent->_parent;
if (parent->_left == brother) {
pos = RIGHT;
}
else {
pos = LEFT;
}
}
}
}
} //删除的节点是父节点的左孩子
else { //cur是父节点的右孩子
if (parent->_right) { //如果cur有孩子,那么一定是红色的,将它变黑
parent->_right->_color = BLACK;
return;
}
else { //cur没有孩子
node* brother = parent->_left;
if (brother->_color == RED) { //brother为红色,调整到brother为黑色的情况
rotateR(parent);
swap(parent->_color, brother->_color);
brother = parent->_left; //调整brother
}
//现在brother为黑色
if (!brother->_left && brother->_right) { //brother左孩子不存在且右孩子存在
rotateL(brother);
swap(brother->_color, brother->_left->_color);
brother = parent->_left;
}
if (brother->_left) { //brother左孩子存在
rotateR(parent);
swap(brother->_color, parent->_color);
brother->_left->_color = BLACK;
return;
}
if (!brother->_left && !brother->_right) { //如果brother没有孩子
if (parent->_color == RED) { //如果父节点是红色的
swap(brother->_color, parent->_color);
return;
}
else { //父节点是黑色的
brother->_color = RED;
brother = parent;
parent = parent->_parent;
if (brother == parent->_left) {
pos = LEFT;
}
else {
pos = RIGHT;
}
}
}
}
}
}//删除的是黑色节点
}
}
private:
node* _root;
bool _compare(const Key& k1, const Key& k2) { return Compare()(k1, k2); }
//析构
void _destructor(node* root) {
if (root == nullptr) return;
_destructor(root->_left);
_destructor(root->_right);
delete root;
root = nullptr;
}
//L就是left,左单旋
void rotateL(node* parent) {
node* subR = parent->_right; // 这就是图中的cur
node* subRL = subR->_left; // cur的左孩子
// parent的右链接cur
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
// parent 链接cur的左
subR->_parent = parent->_parent;
if (parent->_parent) {
node* pParent = parent->_parent;
if (pParent->_left == parent) {
pParent->_left = subR;
}
else {
pParent->_right = subR;
}
}
// cur成为parent
parent->_parent = subR;
subR->_left = parent;
if (parent == _root) {
_root = subR;
}
}
//R就是right, 右单旋
void rotateR(node* parent) {
node* subL = parent->_left;
node* subLR = subL->_right;
//parent的左链接cur
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
// parent链接cur的右
subL->_parent = parent->_parent;
if (parent->_parent) {
node* pParent = parent->_parent;
if (pParent->_left == parent) {
pParent->_left = subL;
}
else {
pParent->_right = subL;
}
}
//cur成为parent
subL->_right = parent;
parent->_parent = subL;
if (parent == _root) {
_root = subL;
}
}
};
检验红黑树的性质
1,是否满足中序遍历为有序。
1,是否满足红黑树自己的4条性质。
//中序遍历
void inOrder(){
_inOrder(_root);
std::cout << endl;
}
//检查红黑树4条性质
bool check(){
if (_root && _root->_color == RED){
return false;
}
//求出一条路径上黑色节点的个数
int num = 0;
node* cur = _root;
while (cur){
if (cur->_color == BLACK){
num++;
}
cur = cur->_left;
}
return RedNode(_root) && BlackNodeNum(_root, 0, num);
}
//子函数
void _inOrder(node* root){
KeyOfValue kof;
if (root == nullptr)
return;
_inOrder(root->_left);
std::cout << kof(root->_value) << " ";
_inOrder(root->_right);
}
//检验是否有连续的红节点,使用的方法是如果孩子为红色,判断父亲是否为红色的,然后向上迭代
bool RedNode(node* root){
if (root == nullptr){
return true;
}
if (root->_color == RED){
//判断父节点是否为红色
if (root->_parent && root->_parent->_color == RED){
return false;
}
}
//判断左右子树
return RedNode(root->_left) && RedNode(root->_right);
}
//检验所有路径的黑色节点数是否相同
bool BlackNodeNum(node* root, int blackNum, int num){
//检查是否每条路径上的黑色节点的个数都相同
if (root == nullptr){
return blackNum == num;
}
if (root->_color == BLACK){
blackNum++;
}
return BlackNodeNum(root->_left, blackNum, num) && BlackNodeNum(root->_right, blackNum, num);
}
set
如果你看过stl的源代码,你会惊讶于一件事情,map和set两种不同的模型,Key模型和Key-Value模型,使用的竟然是同一棵红黑树!这真是magic。红黑树的第二个模板参数value对于set传入的就是K,而对于map传入的是pair
//set,底层封装一颗红黑树,这样的手法叫做适配器
template<class K>
class KeyOfSet { //传入的仿函数,提取出value中的key值
public:
const K& operator()(const K& key) {
return key;
}
};
template<class K, class Compare = greater<K>>
class MySet {
public:
using RBtree = zzh::rbtree<K, K, KeyOfSet<K>, Compare>;
using iterator = typename RBtree::iterator;
iterator begin() {
return _rb.begin();
}
iterator end() {
return _rb.end();
}
pair<iterator, bool> insert(const K& key) {
return _rb.insert(key);
}
void erase(const K& key) {
return _rb.erase();
}
void InOrder() {
_rb.inOrder();
}
private:
RBtree _rb;
};
map
// map
template<class K, class V>
class KeyOfMap { //提取出pair中的key
public:
const K& operator()(const pair<K, V>& kv) {
return kv.first;
}
};
template<class K, class V, class Compare = Greater<K>>
class MyMap {
public:
using RBtree = zzh::rbtree<K, pair<K, V>, KeyOfMap<K, V>, Compare>;
using iterator = typename RBtree::iterator;
iterator begin() {
return _rb.begin();
}
iterator end() {
return _rb.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv) {
return _rb.insert(kv);
}
void erase(const K& key) {
return _rb.erase(key);
}
private:
RBtree _rb;
};
(全文完)