计算机操作系统—经典同步问题
经典同步问题
1.生产者与消费者问题
1.1.问题概述
在现实生活中,当我们缺少某些生活用品时,就会到超市去购买。当你到超市时,你的身份就是消费者,那么这些商品又是哪里来的呢,自然是供应商,那么它们就是生产者,而超市在生产者与消费者之间,就充当了一个交易场所。正是这样的方式才使得人类的交易变得高效,生产者只需要向超市供应商品,消费者只需要去超市购买商品。
计算机是现实世界的抽象,因此像这种人类世界的模型,自然也被引入到了计算机当中。在实际软件开发中,进程或线程就是生产者和消费者,他们分别产生大量数据或消耗大量数据,但是他们之间一般不直接进行交流,而是生产者生产好数据之后把数据交到一个缓冲区中,消费者需要数据时直接从缓冲区中取就可以了。
我们将其总结为 321 原则——3 种关系,2 个角色,1 个场所。
- 3 种关系:生产者与生产者之间是互斥关系,消费者与消费者之间是互斥关系,生产者与消费者之间是同步关系。
- 2 个角色:生产者和消费者。
- 1 个场所:它们之间进行数据交互是在一缓冲区当中,这个缓冲区可以有多种表现形式。
因此,生产者消费者问题问题如下:
一组生产者进程和一组消费者进程共享一个初始为空,大小为 n 的缓冲区,只有缓冲区没有满时,生产者才可以把数据放入缓冲区,否则必须等待;只有缓冲区不空时,消费者才能从中取出数据,否则必须等待。由于缓冲区属于临界资源,它只允许一个生产者放入数据或一个消费者从中取出数据。
1.2.分析
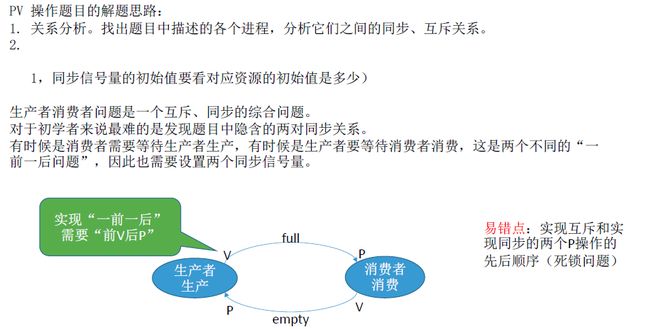
消费者生产者问题是一类很经典的需要使用信号量 (P、V 操作) 来完成互斥和同步的例子,这里 PV 操作题目分析步骤如下:
1.关系分析:找出题目中描述的各个进程,分析它们之间的同步、互斥关系。
- 同步关系:生产者想要放数据必须等待缓冲区没有满;消费者想要取数据必须等待缓冲区没有空。
- 互斥关系:缓冲区为临界资源,各进程必须互斥访问(注意是每一个进程都必须互斥访问)。
2.整理思路:根据各进程的操作流程确定 P、V 操作的大致顺序。
- 这里要注意生产者放入的的确是数据,但是数据占用的是资源,所以生产者放入数据实则是资源的减少过程;同时消费者拿掉数据实则是归还资源的过程。
- 生产者每次消耗 § 一个缓冲区, 并生产 (V) 一个产品;消费者每次消耗 ( P ) 一个产品, 并释放 (V) 一个缓冲区。
- 往缓冲区放入 / 取走产品需要互斥。
3.设置信号量:设置需要的信号量,并根据题目条件确定信号量初值。
- 互斥信号量:初值一般设置为 1。
- 同步信号量:初值要看对应资源的初始值是多少。
所以,设置如下:
semaphore mutex=1;//互斥信号量,实现对缓冲区的互斥访问
semaphore empty=n;//同步信号量,表示空闲缓冲区数量
semaphore full=0;//同步信号量,表示非空闲缓冲区数量,也就是产品数量
1.3.具体代码
实现同步:
- 生产者:将产品放入缓冲区前需要执行 P(empty) 以消耗一个空闲缓冲区;放入缓冲区之后需要执行 V(full) 以增加一个产品数量。
- 消费者:从缓冲区取出产品之前需要执行 P(full) 以消耗一个产品;从缓冲区取出产品之后需要执行 V(empty) 以增加一个空闲缓冲区。
实现互斥:
- 生产者:将产品放入缓冲区前需要执行 P(mutex);放入缓冲区之后需要执行 V(mutex)。
- 消费者:从缓冲区取出产品之前需要执行 P(mutex);从缓冲区取出产品之后 V(mutex)。
因此代码如下:
semaphore mutex=1; //互斥信号量,实现对缓冲区的互斥访问
semaphore empty=n; //同步信号量,表示空闲缓冲区数量
semaphore full=0; //同步信号量,表示非空闲缓冲区数量,也就是产品数量
Producer()
{
while(1)
{
//生产者生产数据
p(empty); //要用什么,P一下 //获取空缓冲区
p(mutex); //互斥夹紧
//将数据放入缓冲区
V(mutex); //互斥夹紧
V(full); //提供什么,V一下 //产品数量增加
}
}
consumer()
{
while(1)
{
p(full);要用什么,P一下 //获取产品
p(mutex):互斥夹紧
//消费者取出产品
V(mutex):互斥夹紧
V(empty):提供什么,V一下 //空缓冲区增加
//消费者使用数据
}
}
思考:能否改变相邻P、V操作的顺序?
1.4.注意
1:实现互斥的 P 操作一定要在实现同步的 P 操作之后
- 如果顺序相反,会导致两个进程同时阻塞,但都希望对方唤醒自己
2:V 操作顺序可以交换,不会导致阻塞
2.多生产者与多消费者问题
2.1.问题描述
- 桌子上有一个盘子,每次只能向其中放入一个水果。
- 爸爸专门放入苹果,妈妈则专门放入橘子。
- 儿子只吃盘子中的橘子,女儿则只吃苹果。
- 只有盘子空时,爸爸或妈妈才可以放入水果;只有盘子中有自己需要的水果时,儿子或女儿才可以取出水果。
- 使用 PV 操作实现上述过程。
2.2.问题分析
关系分析:找出题目中描述的各个进程,分析它们之间的同步、互斥关系。
- 互斥关系:爸爸和妈妈是互斥关系,他们对于缓冲区,也就是盘子的访问要互斥进行。
- 同步关系:爸爸和女儿是同步关系,妈妈和儿子也是同步关系,这两对进程必须连起来。
- 儿子和女儿没有关系,盘子为空这个事件可以由儿子或女儿触发,事件发生后才允许父亲或母亲放水果。
整理思路:根据各进程的操作流程确定 P、V 操作的大致顺序。
- 4 个进程其本质是两个生产和两个消费者被连接到大小为 1 的缓冲区上。
- 实现互斥需要在临界区前后分别进行 P、V;实现同步需要 “前 V 后 P”。
设置信号量:设置需要的信号量,并根据题目条件确定信号量初值。
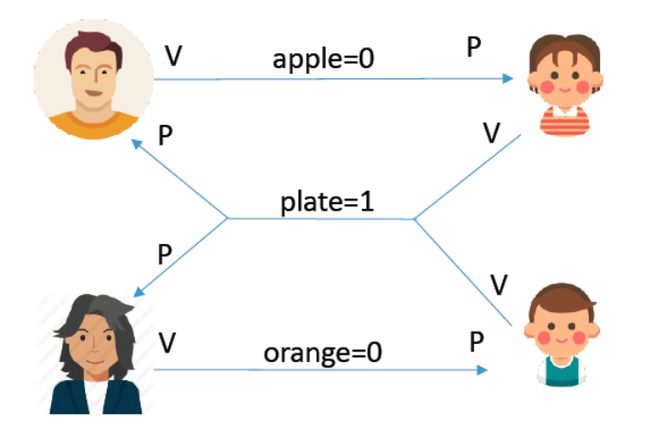
- 互斥信号量:将 plate 设置为 1,表示是否允许向盘子放入水果,初值为 1 表示允许且只能放入一个。
- 同步信号量:信号量 apple 表示盘子中是否有苹果,初值为 0,不许取,若为 1 表示可以取;信号量 red 表示盘子中是否有橘子,初值为 0,不许取,若为 1 表示可以取。
semaphore mutex 1;//实现互斥访问盘子(缓冲区) 可省略,具体解释看下一节
semaphore plate=1;//盘子中还可以放多少个水果
semaphore apple=0;//盘子中有几个苹果
semaphore red=0;//盘子中有几个橘子
2.3.代码实现
semaphore mutex 1;//实现互斥访问盘子(缓冲区) 可省略,具体解释看下一节
semaphore plate=1;//盘子中还可以放多少个水果
semaphore apple=0;//盘子中有几个苹果
semaphore red=0;//盘子中有几个橘子
dad()
{
while(1)
{
准备一个苹果;
P(plate);//互斥放水果
向盘子中放苹果;
V(apple);//可以取苹果
}
}
mom()
{
while(1)
{
准备一个橘子;
P(plate);//互斥放水果
向盘子中放橘子;
V(red);//允许取橘子
}
}
son()
{
while(1)
{
P(red);//互斥从盘子中取橘子
取橘子
V(plate);//取完归还盘子
吃橘子
}
}
daughter()
{
while(1)
{
P(apple);//互斥从盘子中取苹果
取苹果
V(plate);//取完归还盘子
吃苹果
}
}
因此,刚开始时,儿子、女儿进程即使先上处理机也会因为没有相应的水果而被阻塞。假设父亲先上处理机运行,则父亲会执行 P(Plate),可以访问盘子,而母亲执行了 P(Plate) 会被阻塞;父亲放入苹果, 执行了 V(apple), 女儿进程被唤醒,其他进程即使运行也会被阻塞;女儿执行了 V(apple) 后再 V(Plate) 会唤醒等待盘子的母亲进程,接着母亲再继续访问盘子…
2.3.注意
该问题只设置了一个互斥变量 Plate 就可以达到目的,而并没有设置专门的互斥变量 mutex。这是因为:本题缓冲区大小为 1,盘子中只能放一个水果,在任何时刻,apple、red、plate 三个同步信号量中最多只有一个是 1,因此在任何时刻,最多只有一个进程的 P 操作不会被阻塞,并顺利进入临界区。
如果将 plate 设置为 2, 那么父亲访问盘子时,将 plate 减少为了 1,于是母亲也可以访问盘子,而多个生产者如果不互斥访问缓冲区就可能会造成数据覆盖的问题,所以在这种情况下就必须设置一个 mutex=1 来保证互斥访问缓冲区。
semaphore plate=2;
另外,在分析同步问题的时候不能从单个进程行为的角度进行分析,要把一前一后发生的事看作两种事件的前后关系。
上面的例子中看似有以下 4 对关系:
- 女儿取走苹果父亲才能放入水果。
- 女儿取走苹果母亲才能放入水果。
- 儿子取走橘子父亲才能放入水果。
- 儿子取走橘子母亲才能放入水果。
实则不然,它体现的仅仅是 “盘子变空事件” 和“放入水果事件”这两个事件的前后关系(盘子变空必须在放入水果之前),所以只需要一个 plate 就可以解决问题了,而不需要更多的信号量。
3.吸烟者问题
3.1.问题描述
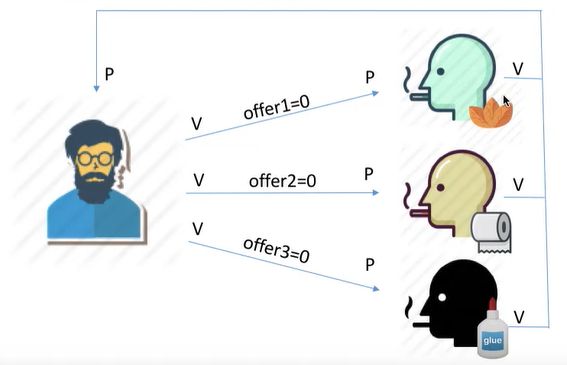
- 一个系统中有三个抽烟者进程和一个供应者进程(供应原材料)。
- 每个抽烟者不停卷烟然后抽掉,但是要卷起并抽掉一支烟,需要三种材料:烟草、纸和胶水。
- 这个三个抽烟者中:第一个拥有烟草;第二个拥有纸;第三个则拥有胶水。
- 供应者每次将两种材料放在桌子上,拥有剩下那种材料的抽烟者便会卷起烟抽掉,然后给供应者进程一个信号以示完成。
- 接着供应者就会把另外两种材料再放在桌子上。
- 此过程一直重复进行,需要让三个抽烟者轮流吸烟。
这道题本质也属于生产者 - 消费者问题,具体来说是:可生产多种产品的单生产者 - 多消费者问题,另外需要注意生产者向桌子上放得材料要理解为单位 “1”,也可以说是一个组合。
- 组合一:纸 + 胶水。
- 组合二:烟草 + 胶水。
- 组合三:烟草 + 纸。
3.2.问题分析
关系分析:找出题目中描述的各个进程,分析它们之间的同步、互斥关系。
- 互斥关系:桌子可以抽象为容量为 1 的缓冲区,需要进行互斥访问。
- 同步关系:桌子上有组合一 / 二 / 三时,第一 / 二 / 三个抽烟者取走东西,这是三个同步关系;还有抽烟者抽完烟之后要发出完成信号,这是第四个同步关系。
整理思路:根据各进程的操作流程确定 P、V 操作的大致顺序。
- 实现互斥需要在临界区前后分别进行 P、V;实现同步需要 “前 V 后 P”。
设置信号量:设置需要的信号量,并根据题目条件确定信号量初值:
- 互斥信号量:该问题由于缓冲区大小为 1,所以可以不设置互斥信号量。
- 同步信号量:信号量 offer1、offer2 及 offer3 对应组合一、二及三,初值均为 0,生产者需要执行 V 操作,消费者需要执行 P 操作;信号量 finish 可以由三个消费者中任意一个发出,提醒生产者可以放材料,初值为 0,生产者执行 P 操作,消费者执行 V 操作。
- 桌上有组合一 → 第一个抽烟者取走东西 桌上有组合一→第一个抽烟者取走东西 桌上有组合一→第一个抽烟者取走东西
- 桌上有组合二 → 第二个抽烟者取走东西 桌上有组合二→第二个抽烟者取走东西 桌上有组合二→第二个抽烟者取走东西
- 桌上有组合三 → 第三个抽烟者取走东西 桌上有组合三→第三个抽烟者取走东西 桌上有组合三→第三个抽烟者取走东西
- 发出完成信号 → 供应者将下一个组合放到桌上 发出完成信号→供应者将下一个组合放到桌上 发出完成信号→供应者将下一个组合放到桌上
semaphore offer1=0;//组合一的数量
semaphore offer2=0;//组合二的数量
semaphore offer3=0;//组合三的数量
semaphore finish=0;//抽烟是否完成
int i=0;//用于实现轮流抽烟
3.3.代码实现
对于生产者,其内部进行逻辑判断,利用取余的方式轮流放置组合一、二和三,放置完成之后如果消费者不执行 V(finish),它将会在 P(finish) 处被阻塞。
provider
{
while(1)
{
if(i==0)
{
组合一放桌子上
V(offer1);
}
else if(i==1)
{
组合二放桌子上
V(offer2);
}
else if(i==2)
{
组合三放桌子上
V(offer3);
}
i=(i+1)%3;
P(finish);
}
}
对于这三个消费者,他们各自在进入时首先会检查是否有自己的组合,如果没有将会被阻塞,如果有,执行完毕之后使用 V(finish) 通知生产者生产。
smoker1()
{
while(1)
{
P(Offer1);
一系列卷烟、抽烟操作、拿走组合一
V(finish);
}
}
smoker2()
{
while(1)
{
P(Offer2);
一系列卷烟、抽烟操作、拿走组合二
V(finish);
}
}
smoker3()
{
while(1)
{
P(Offer3);
一系列卷烟、抽烟操作、拿走组合三
V(finish);
}
}
是否需要设置一个专门的互斥信号量?
否,缓冲区大小为1,同一时刻,四个同步信号量中至多有一个的值为1。
4.读者写者问题
4.1.问题描述
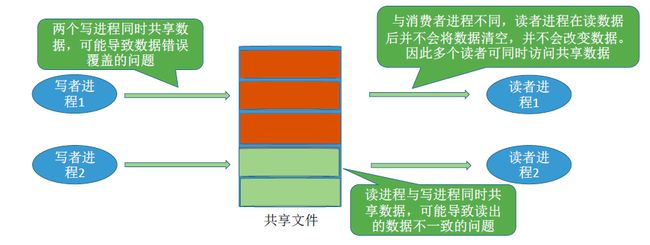
读者和写者两组并发进程,共享一个文件,它们访问时有如下特点:
- 多个读进程访问共享数据时不会产生副作用。
- 如果某个写进程和其他进程(读进程或写进程)同时访问共享数据时,会导致数据不一致的错误。
所以为了使访问正常进行,必须要求:
- 允许多个读者可以同时对文件执行读操作。
- 只允许一个写者向文件中写信息。
- 任何一个写者在完成写操作之前不允许其他读者或写者工作。
- 写者执行写操作时,应该让已有的读者和写者全部退出。
4.2.问题分析
关系分析:找出题目中描述的各个进程,分析它们之间的同步、互斥关系。
- 互斥关系:写进程与写进程;写进程与读进程。
- 同步关系:没有同步关系,只有互斥关系。
整理思路:根据各进程的操作流程确定 P、V 操作的大致顺序。
- 对于写者来说,它与任何进程都是互斥的,因此可以设置一个互斥信号量 rw,在写者访问共享文件前后分别执行 P、V 操作。
- 对于读者进程,如果它也像前面那样,那么就不符合读者进程可以同时访问文件的要求了。既然各个读进程需要同时访问,而读进程与写进程又必须互斥访问,所以我们可以让第一个访问文件的读进程 “加锁”,也就是 P 操作,然后让最后一个访问完文件的读进程进行解锁,也就是 V 操作。所以可以设置一个整形变量 count 来记录当前有几个读进程在访问文件。
- 对于读进程来说,在某一时刻多个读进程并发执行。而我们对 count 变量的判断是无法实现原子性操作的,所以这里 count 就是一种临界资源了,需要对其进行保护,可以设置互斥信号量 mutex。
设置信号量:设置需要的信号量,并根据题目条件确定信号量初值。
- 设置信号量
count为计数器,用于记录当前读者的数量,初值为 0; - 设置
mutex为互斥信号量,用于保护更新 count 变量时的互斥; - 设置互斥信号量
rw,用于保证读者和写者的互斥访问。
int count=0; //用于记录当前的读者数量
semaphore mutex=1; //用于保护更新count变量时的互斥
semaphore rw=1; //用于保证读者和写者互斥地访问文件
4.3.代码实现
对于写者,在写文件之前进行 P 操作,写完之后进行 V 操作,就可以实现写者与其他进程的互斥。
writer() //写者进程
{
while(1)
{
P(rw);//写之前加锁 //互斥访问共享文件
写文件;
V(rw);//写之后解锁 //释放共享文件
}
}
对于读者,第一个读者进入会加锁,最后一个读者退出时进行解锁。
思考:若两个读进程并发执行,则count=0时两个进程也许都能满足if条件,都会执行P(rw),从而使第二个读进程阻塞的情况。
如何解决:出现上述问题的原因在于对count变量的检查和赋值无法一气呵成,因此可以设置另一个互斥信号量(mutex)来保证各读进程对count的访问是互斥的。
reader() //读者进程
{
while(1)
{
P(mutex);//使用P操作保护count,防止多个读进程对临界资源的操作//互斥访问count变量
if(count==0) //当第一个读进程读共享文件时
P(rw);//第一个读进程 //阻止写进程写
count++; //读者计数器加1
V(mutex); //释放互斥变量count
读文件;
P(mutex); //互斥访问count变量
count--; //读者计数器减1
if(count==0) //当最后一个读进程读完共享文件
V(rw);//最后一个读进程 //允许写进程写
V(mutex); //释放互斥变量count
}
}
但是上面代码还存在一个 bug:读进程是优先,只要有读进程在读,写进程就会一直被阻塞,写进程饿死。
所以如果希望写进程优先,也就是说当有读进程在读时,若有写进程请求访问,那么应该禁止后续读进程请求,等到本次读进程完毕之后,立即让写进程执行,只有在无写进程的情况下才允许读进程再次运行。因此可以再增设一个信号量 w,用于实现写优先。
int count=0; //用于记录当前的读者数量
semaphore mutex=1; //用于保护更新count变量时的互斥
semaphore rw=1; //用于保证读者和写者互斥地访问文件
semaphore w=1; //用于实现“写优先”
writer() //写者进程
{
while(1)
{
P(w); //在无写进程请求时进入
P(rw); //互斥访问共享文件
写文件;
V(rw); //释放共享文件
V(w); //恢复对共享文件的访问
}
}
reader() //读者进程
{
while(1)
{
p(w); //在无写进程请求时进入
P(mutex); //互斥访问count变量
if(count==0) //当第一个读进程读共享文件时
P(rw); //阻止写进程写
count++; //读者计数器加1
V(mutex); //释放互斥变量count
V(w); //恢复对共享文件的访问
写文件;
P(mutex); //〃互斥访问count变量
count--; //读者计数器减1
if(count==0) //当最后一个读进程读完共享文件
V(rw); //允许写进程写
V(mutex); //释放互斥变量count
}
}
- 如果读者 1、读者 2 陆续进入,由于没有写者进入,(reader 中)因此后续读者也能够正常进入。
- 如果写者 1、写者 2 陆续进入,因此在 writer 中,第一个写者进入后会把第二写者阻塞。
- 如果是写者 1、读者 1陆续进入,那么在写者 1 进入后,读者 1 就无法进入,直到写者 1 释放资源。
- 如果是读者 1、写者 1、读者 2陆续进入,那么在读者 1 执行完
V(w)后,写者 1 不会被阻塞在P(w),但是由于读者 1 执行了P(rw),所以此时写者 1 会被阻塞在P(rw)处,而当读者 2 执行时,由于写者 1 已经执行了P(w)而没有执行V(w),所以读者 2 会被阻塞P(w)处,直到读者 1 进行V(rw)后,所以写者 1 就会在P(rw)处唤醒,继续执行,但是读者 2 还是被阻塞在P(w)处,当写者 1V(w)后,读者 2 便可以继续进行。 - 如果是写者1、读者 1、写者 2陆续进入,那么在写者 1执行完
P(w)和P(rw)后, 读者1执行了P(w),所以读者1会被阻塞在P(w)处。此时如果有写者2进入,写者2也会被阻塞在P(w)处。由于读者1先对w执行了P操作,所以读者1会先排在w这个互斥信号量后面的队列中,它处于队头的位置;而接下来写者2是之后对w进行P操作的,所以写者2会被排在读者1之后,因此当写者1写完文件并且对w这个信号量执行V操作的时候,它唤醒的是先到来的读者1,而不是后到来的写者2,读者1继续进行。
结论:在这种算法中,连续进入的多个读者可以同时读文件;写者和其他进程不能同时访问文件;写者不会饥饿,但也并不是真正的“写优先”,而是相对公平的先来先服务原则。有的书上把这种算法称为“读写公平法”。
读者-写者问题有一个关键的特征,即有一个互斥访问的计数器cout,因此遇到一个不太好解决的同步互斥问题时,要想一想用互斥访问的计数器cout能否解决问题。
5.哲学家进餐问题
- 哲学家进餐问题的关键在于解决进程死锁。
- 这些进程之间只存在互斥关系,但是与之前接触到的互斥关系不同的是,每个进程都需要同时持有两个临界资源,因此就有“死锁”问题的隐患。
- 如果在考试中遇到了一个进程需要同时持有多个临界资源的情况,应该参考哲学家问题的思想,分析题中给出的进程之间是否会发生循环等待,是否会发生死锁。
- 可以参考哲学家就餐问题解决死锁的三种思路。
5.1.问题描述
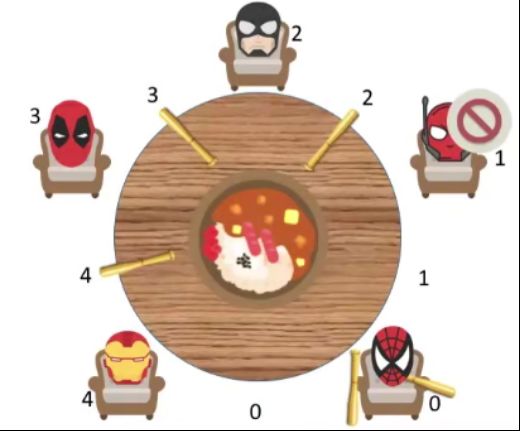
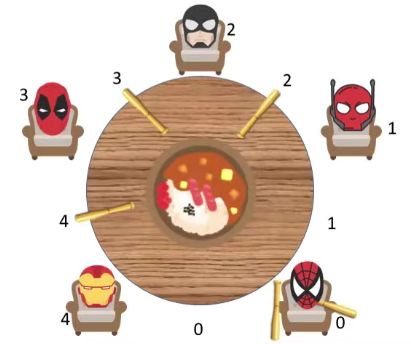
- 一张圆桌上坐着 5 名哲学家,每两个哲学家之间的桌上摆一根筷子,桌子中间是一碗米饭。
- 哲学家只干两件事情:思考和进餐。
- 哲学家在思考时,不影响别人。
- 哲学饥饿时,才试图拿起左、右两根筷子(一根一根拿起),如果筷子已经在他人的手上,则需要等待。
- 饥饿的哲学家只有同时拿起两根筷子才可以开始进餐。
- 进餐完毕后,放下筷子继续思考。

5.2.问题分析
关系分析:找出题目中描述的各个进程,分析它们之间的同步、互斥关系。
- 互斥关系:5 位哲学家是互斥访问筷子。
- 同步关系:没有同步关系,只有互斥关系。
整理思路:根据各进程的操作流程确定 P、V 操作的大致顺序。
- 此问题中只存在互斥关系,但是相比之前的问题,这里每位哲学需要同时持有两个临界资源才能开始吃饭,如果资源分配不当会造成死锁。
设置信号量:设置需要的信号量,并根据题目条件确定信号量初值。
-
定义互斥信号量数组 chopsticks[5]={1,1,1,1,1} 用于实现对 5 根筷子的互斥访问。
-
对哲学家按照 0~4 依次编号,哲学家 i i i 左边的筷子编号为 i i i,右边的筷子编号为$ (i+1)%5$ 。

因此在这种信号量设置下,可以用下面这样的代码实现。
semaphore chopsticks[5]={1,1,1,1,1};
P i()//i号哲学家进程
{
while(1)
{
P(chopsticks[i]);//拿左
P(chopsticks[i+1]%5);//拿右
吃饭
V(chopsticks[i]);//拿左
V(chopsticks[i+1]%5);//拿右
思考
}
}
但是这样实现有一些问题:当 5 名哲学家都想要进餐并分别拿起左边的筷子时,等到他们想要拿起右边筷子时,发现已经没有筷子了,于是每一位哲学家都在等待右边的人放下筷子,发生了死锁。
如何防止死锁的发生呢?
-
可以对哲学家进程施加一些限制条件,比如最多允许四个哲学家同时进餐。这样可以保证至少有一个哲学家是可以拿到左右两只筷子的。
比如说此时我们只允许0123这四个哲学家同时进餐,那么即使这些哲学家并发的执行。那即使每一个哲字家先都已经拿起了自已身边的一只筷子,但是最后肯定还会有一只筷子是剩余的,这只筷子只要分配给与他相邻的这个哲字家,那么这个哲学家就可以拥有两只筷子,并且顺利的吃饭,等他吃完饭之后,把这两个筷子放下了,那么其他的这些哲学家就依次又可以被激活,所以如果我们用这种方案的话,就可以保证至少会有一个哲学家是可以拿到左右两只筷子的,因为筷子总共有五只,而我们只最多只允许四个哲学家同时进餐。所以这种方案是可行的。第一个方案要实现最多允许四个哲学家同时进餐的话,那么我们可以设置一个初始值为四的同步信号量。
-
要求奇数号哲学家先拿左边的筷子,然后再拿右边的筷子,而偶数号哲学家刚好相反。用这种方法可以保证如果相邻的两个奇偶号哲学家都想吃饭,那么只会有其中一个可以拿起第一只筷子,另一个会直接阻塞。这就避免了占有一支后再等待另一只的情况。
第二种方案,我们可以做一个这样的限制,对于基数号的哲学家来说,他必须先拿自己左边的这只筷子。而对于偶数号的哲学家来说,他必须先拿右边的这双筷子,如果做了这样的限制,那么两个哲学家,他们首先会争抢着使用他们之间的这只筷子。所以如果我们加上这样的规则的话,我们就可以保证两个相邻的奇偶号哲学家,如果他们同时都想吃饭的话。那么,他们首先会优先的竟争,争抢他们之间的这一支筷子,那肯定只会有一个哲学家可以得到这个筷子资源,那另一个哲学家如果争抢失败。那么他就会在手里没有筷子的情况下就发生阻塞的现象,而不会像刚才一样,手里拿了一只筷子,同时又发生了阻塞,这样的话,我们就可以避免一个进程在占有了一个资源之后还要等待另一个资源这样的现象,从而我们就能避免死锁现象的发生。如何代码实现:我们可以在每一个哲学家拿筷子之前先判断一下它们的序号到底是奇数号还是偶数号,然后再根据自己的这个序号来做下面的一些处理。
-
仅当一个哲学家左右两支筷子都可用时才允许他抓起筷子。
5.3.代码实现
因此为了防止死锁发生,我们可以施加一些限制条件:当一名哲学家左右筷子都可用时,才允许它拿起筷子
semaphore chopsticks[5]={1,1,1,1,1};
semaphore mutex=1;//取筷子信号量
P i()//i号哲学家进程
{
while(1)
{
P(mutex):
P(chopsticks[i]);//拿左
P(chopsticks[i+1]%5);//拿右
V(mutex);
吃饭
V(chopsticks[i]);//放左
V(chopsticks[i+1]%5);//放右
思考
}
}
可以设置一个互斥信号量mutex,然后在哲学家拿筷子之前和拿完筷子之后分别对这个互斥信号量执行P和V两个操作。我们具体来分析一下,如果用这样的代码的话啊,会发生什么情况?
假设现在是0号哲学家在尝试拿筷子,那么首先他对mutex执行P操作,显然不会被阻塞,于是他可以开始拿第一只筷子,对第一个筷子对应的互斥信号量执行P操作。当这个P操作结束之后,他就拥有了这只筷子。此时如果说发生了进程切换,切换回了2号哲学家进程。那么,当2号哲学家对mutex执行P操作的时候,由于0号哲学家还没有对mutex执行V操作,所以2号哲学家在执行mutex的时候,暂时会被阻塞,一直到再切换回0号哲学家,并且他顺利的拿到了右边这只筷子,再对这个mutex执行V操作之后,2号哲学家又可以被激活,然后他就可以顺利的开始执行下面的这两个P操作,也就是分别拿起自己左边和右边的两只筷子。所以通过刚才的分析,我们发现一个哲学家左右两边的筷子都可以用的时候他是可以一气呵成的,依次拿左右两只筷子的。
再来看第二种情况,假设刚开始是0号哲学家在运行,他打算吃饭,那么他会顺利的通过第一个P操作,然后拿起第一只筷子,再拿起第二只筷子,再对mutex进行V操作,于是他可以顺利的开始吃饭,但是如果在这个时候1号哲学家,他也想吃饭,并不会把它阻塞,他可以顺利的通过P操作,但是当1号哲学家尝试拿左边的这只筷子的时候,它就会发生阻塞,它会卡在这个地方。
而此时,如果说再发生调度2号哲学家开始运行,那么2号哲学家他也想吃饭,于是他会尝试着对mutex执行P操作。
由于之前1号哲学家已经对mutex执行了一个P操作,并且暂时还没有释放。所以2号哲学家在之后执行mutex的P操作的时候,他会被阻塞。它会被阻塞在这个地方。
所以如果从这种情况下来看,即使2号哲学家此时左右两边的筷子其实都可以用,但是这个哲学家依然拿不起他两边的筷子。它依然有可能会被阻塞。
再来看第三种情况。如果说刚开始是0号哲学家拿了左边的筷子和右边的筷子,然后0号哲学家开始吃饭。
之后,4号哲学家,他也尝试拿左边的筷子,由于左边的筷子暂时没人用,所以他可以拿起来,但是当他在尝试拿右边的这只筷子的时候,由于这只筷子此时已经被别的哲学家拿走了。所以四号哲学家也会发生阻塞,阻塞在这个地方。
所以如果在这种情况下,4号哲学家拿了一只筷子的同时,在等待别的筷子,因此通过刚才的这两种情况的分析,我们发现。虽然咱们的书上说的是只有两边的筷子都可以用时才允许哲学家拿起筷子。但其实,即使一个哲学家两边的筷子其中某一边不能用的情况下,这个哲学家依然有可能拿起其中的一只筷子,所以这种说法其实是不太严谨的。
更准确的说法应该是:我们用这个互斥信号保证了每个哲学家拿筷子这件事都是互斥的进行的。如果一个哲学家正在拿筷子,不管是拿左边还是拿右边,那么另一个哲学家就不允许同时来做拿筷子这样的操作。如果一个哲学家因为拿筷子的过程中被阻塞了,那么其他的哲学家在尝试拿筷子的时候,他连这个P操作都过不了,就会被阻塞在外面这一层。所以所有的哲学家拿筷子这一个操作都是可以互斥的执行的,那么由于这种特性,我们就可以保证,即使一个哲学家在拿筷子拿到一半的时候被阻塞,也不会有别的哲学家再继续拿筷子,既然这个哲学家被阻塞了,那就意味着肯定有另外的哲学家现在手里已经持有了他所需要的筷子,那只要这个哲学家吃完饭把筷子还到原位之后,这个哲学家就可以拿起他所需要的另一只筷子,然后顺利的吃饭,然后之后再把他手里的两个筷子再释放。所有的哲学家就可以一次的被激活,这样的话就可以避免循环等待发生。死锁的那种现象。因此,这种解决方案是可行的,它并不会发生死锁。