Verilog 学习笔记(6)——竞争与冒险、latch、verilog书写规范
本章介绍竞争与冒险及其消除方法,latch产生的原因及避免方法,最后总结verilog要注意的一些书写规范。
文章目录
- 6.1 Verilog 竞争与冒险
-
- 产生原因
- 判断方法
-
- 代数法
- 卡诺图法
- 消除方法
- 6.2 Verilog 避免 Latch
-
- Latch 的含义
-
- if 结构不完整
- case 结构不完整
- 原信号赋值或判断
- 敏感信号列表不完整
- 小结
- 6.3 Verilog 书写规范
-
- 1)时序电路建模时,用非阻塞赋值
- 2)组合逻辑建模时,用阻塞赋值
- 3)在同一个 always 块中建立时序和组合逻辑模型时,用非阻塞赋值
- 4)在同一个 always 块中不要既使用阻塞赋值又使用非阻塞赋值
- 5)不要在多个 always 块中为同一个变量赋值
- 6)避免 latch 产生
6.1 Verilog 竞争与冒险
产生原因
数字电路中,信号传输与状态变换时都会有一定的延时。
- 在组合逻辑电路中,不同路径的输入信号变化传输到同一点门级电路时,在时间上有先有后,这种先后所形成的时间差称为竞争(Competition)。
- 由于竞争的存在,输出信号需要经过一段时间才能达到期望状态,过渡时间内可能产生瞬间的错误输出,例如尖峰脉冲。这种现象被称为冒险(Hazard)。
- 竞争不一定有冒险,但冒险一定会有竞争。
例如,对于给定逻辑F = A & A',电路如左下图所示。
由于反相器电路的存在,信号 A’ 传递到与门输入端的时间相对于信号 A 会滞后,这就可能导致与门最后的输出结果 F 会出现干扰脉冲。如右下图所示。
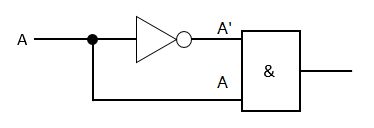
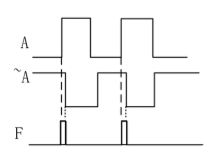
其实实际硬件电路中,只要门电路各个输入端延时不同,就有可能产生竞争与冒险。
例如一个简单的与门,输入信号源不一定是同一个信号变换所来,由于硬件工艺、其他延迟电路的存在,也可能产生竞争与冒险,如下图所示。
判断方法
代数法
在逻辑表达式,保持一个变量固定不动,将剩余其他变量用 0 或 1 代替,如果最后逻辑表达式能化简成Y = A + A’ 或者Y = A · A’ 的形式,则可判定此逻辑存在竞争与冒险。
例如逻辑表达式 Y = AB + A’C,在 B=C=1 的情况下,可化简为 Y = A + A’。显然,A 状态的改变,势必会造成电路存在竞争冒险。
卡诺图法
有两个相切的卡诺圈,并且相切处没有其他卡诺圈包围,可能会出现竞争与冒险现象。
例如左下图所存在竞争与冒险,右下图则没有。

其实,卡诺图本质上还是对逻辑表达式的一个分析,只是可以进行直观的判断。
例如,左上图逻辑表达式可以简化为 Y = A’B’ + AC,当 B=0 且 C=1 时,此逻辑表达式又可以表示为 Y = A’ + A。所以肯定会存在竞争与冒险。
右上图逻辑表达式可以简化为 Y = A’B’ + AB,显然 B 无论等于 1 还是 0,此式都不会化简成 Y = A’ + A。所以此逻辑不存在竞争与冒险。
需要注意的是,卡诺图是首尾相临的。如下图所示,虽然看起来两个卡诺圈并没有相切,但实际上,m6 与 m4 也是相邻的,所以下面卡诺图所代表的数字逻辑也会产生竞争与冒险。
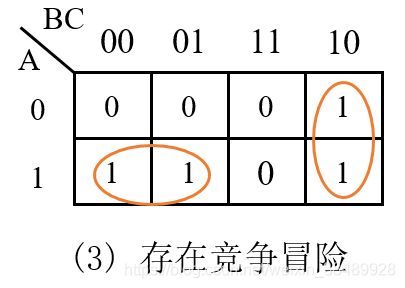
其他较为复杂的情况,可能需要采用 “计算机辅助分析 + 实验” 的方法。
消除方法
对数字电路来说,常见的避免竞争与冒险的方法主要有 4 种。
1)增加滤波电容,滤除窄脉冲
此种方法需要在输出端并联一个小电容,将尖峰脉冲的幅度削弱至门电路阈值以下。
此方法虽然简单,但是会增加输出电压的翻转时间,易破坏波形。
2)修改逻辑,增加冗余项
利用卡诺图,在两个相切的圆之间,增加一个卡诺圈,并加在逻辑表达式之中。
如下图所示,对数字逻辑 Y = A’B’ + AC 增加冗余项 B’C,则此电路逻辑可以表示为 Y = A’B’ + AC + B’C。此时电路就不会再存在竞争与冒险。

3)使用时钟同步电路,利用触发器进行打拍延迟
同步电路信号的变化都发生在时钟边沿。对于触发器的 D 输入端,只要毛刺不出现在时钟的上升沿并且不满足数据的建立和保持时间,就不会对系统造成危害,因此可认为 D 触发器的 D 输入端对毛刺不敏感。 利用此特性,在时钟边沿驱动下,对一个组合逻辑信号进行延迟打拍,可消除竞争冒险。
延迟一拍时钟时,会一定概率的减少竞争冒险的出现。实验表明,最安全的打拍延迟周期是 3 拍,可有效减少竞争冒险的出现。
当然,最终还是需要根据自己的设计需求,对信号进行合理的打拍延迟。
为说明对信号进行打拍延迟可以消除竞争冒险,我们建立下面的代码模型。
module competition_hazard
(
input clk ,
input rstn ,
input en ,
input din_rvs ,
output reg flag
);
wire condition = din_rvs & en ; //combination logic
always @(posedge clk or negedge !rstn) begin
if (!rstn) begin
flag <= 1'b0 ;
end
else begin
flag <= condition ;
end
end
endmodule
testbench 描述如下:
`timescale 1ns/1ns
module test ;
reg clk, rstn ;
reg en ;
reg din_rvs ;
wire flag_safe, flag_dgs ;
//clock and rstn generating
initial begin
rstn = 1'b0 ;
clk = 1'b0 ;
#5 rstn = 1'b1 ;
forever begin
#5 clk = ~clk ;
end
end
initial begin
en = 1'b0 ;
din_rvs = 1'b1 ;
#19 ; en = 1'b1 ;
#1 ; din_rvs = 1'b0 ;
end
competition_hazard u_dgs
(
.clk (clk ),
.rstn (rstn ),
.en (en ),
.din_rvs (din_rvs ),
.flag (flag_dgs ));
initial begin
forever begin
#100;
if ($time >= 1000) $finish ;
end
end
endmodule // test
仿真结果如下:

由图可知,信号 condition 出现了一个尖峰脉冲,这是由于信号 din_rvs 与信号 en 相对于模块内部时钟都是异步的,所以到达内部门电路时的延时是不同的,就有可能造成竞争冒险。
虽然最后的仿真结果 flag 一直为 0,似乎是我们想要的结果。但是实际电路中,这个尖峰脉冲在时间上非常靠近时钟边沿,就有可能被时钟采集到而产生错误结果。
下面我们对模型进行改进,增加打拍延时的逻辑,如下:
module clap_delay
(
input clk ,
input rstn ,
input en ,
input din_rvs ,
output reg flag
);
reg din_rvs_r ;
reg en_r ;
always @(posedge clk or !rstn) begin
if (!rstn) begin
din_rvs_r <= 1'b0 ;
en_r <= 1'b0 ;
end
else begin
din_rvs_r <= din_rvs ;
en_r <= en ;
end
end
wire condition = din_rvs_r & en_r ;
always @(posedge clk or negedge !rstn) begin
if (!rstn) begin
flag <= 1'b0 ;
end
else begin
flag <= condition ;
end
end // always @ (posedge clk or negedge !rstn)
endmodule
将此模块例化到上述 testbench 中,得到如下仿真结果。

由图可知,信号 condition 没有尖峰脉冲的干扰了,仿真结果中 flag 为 0 也如预期。
其实,输入信号与时钟边沿非常接近的情况下,时钟对输入信号的采样也存在不确定性,但是不会出现尖峰脉冲的现象。对输入信号多打 2 拍,是更好的处理方式,对竞争与冒险有更好的抑制作用。
4)采用格雷码计数器
递加的多 bit 位计数器,计数值有时候会发生多个 bit 位的跳变。
例如计数器变量 counter 从 5 计数到 6 时, 对应二进制数字为 4’b101 到 4’b110 的转换。因为各 bit 数据位的延时,counter 的变换过程可能是: 4’b101 -> 4’b111 -> 4’b110。如果有以下逻辑描述,则信号 cout 可能出现短暂的尖峰脉冲,这显然是与设计相悖的。
cout = counter[3:0] == 4'd7 ;
而格雷码计数器,计数时相邻的数之间只有一个数据 bit 发生了变化,所以能有效的避免竞争冒险。
好在 Verilog 设计时,计数器大多都是同步设计。即便计数时存在多个 bit 同时翻转的可能性,但在时钟驱动的触发器作用下,只要信号间满足时序要求,就能消除掉 100% 的竞争与冒险。
小结
- 一般来说,为消除竞争冒险,增加滤波电容和逻辑冗余,都不是 Verilog 设计所考虑的。
- 计数采用格雷码计数器,大多数也是应用在高速时钟下减少信号翻转率来降低功耗的场合。
- 利用触发器在时钟同步电路下对异步信号进行打拍延时,是 Verilog 设计中经常用到的方法。
除此之外,为消除竞争冒险,Verilog 编码时还需要注意一些问题,详见下一小节。
6.2 Verilog 避免 Latch
Latch 的含义
锁存器(Latch),是电平触发的存储单元,数据存储的动作取决于输入时钟(或者使能)信号的电平值。仅当锁存器处于使能状态时,输出才会随着数据输入发生变化。
当电平信号无效时,输出信号随输入信号变化,就像通过了缓冲器;当电平有效时,输出信号被锁存。激励信号的任何变化,都将直接引起锁存器输出状态的改变,很有可能会因为瞬态特性不稳定而产生振荡现象。
锁存器示意图如下:
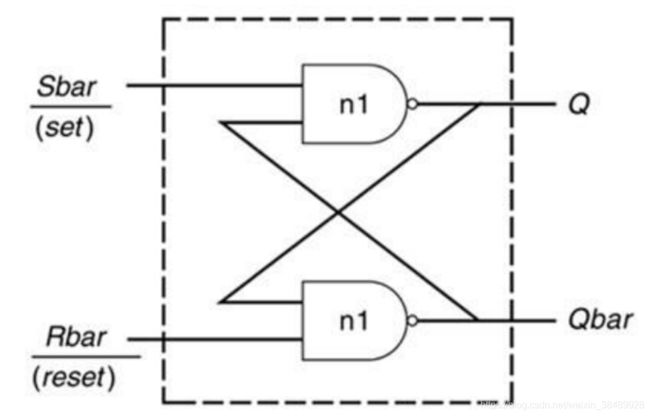
触发器(flip-flop),是边沿敏感的存储单元,数据存储的动作(状态转换)由某一信号的上升沿或者下降沿进行同步的(限制存储单元状态转换在一个很短的时间内)。
触发器示意图如下:

寄存器(register),*在 Verilog 中用来暂时存放参与运算的数据和运算结果的变量。*一个变量声明为寄存器时,它既可以被综合成触发器,也可能被综合成 Latch,甚至是 wire 型变量。但是大多数情况下我们希望它被综合成触发器,但是有时候由于代码书写问题,它会被综合成不期望的 Latch 结构。
Latch 的主要危害有:
- 1)输入状态可能多次变化,容易产生毛刺,增加了下一级电路的不确定性;
- 2)在大部分 FPGA 的资源中,可能需要比触发器更多的资源去实现 Latch 结构;
- 3)锁存器的出现使得静态时序分析变得更加复杂。
Latch 多用于门控时钟(clock gating)的控制,一般设计时,我们应当避免 Latch 的产生。
if 结构不完整
组合逻辑中,不完整的 if - else 结构,会产生 latch。
例如下面的模型,if 语句中缺少 else 结构,系统默认 else 的分支下寄存器 q 的值保持不变,即具有存储数据的功能,所以寄存器 q 会被综合成 latch 结构。
module module1_latch1(
input data,
input en ,
output reg q) ;
always @(*) begin
if (en) q = data ;
end
endmodule
避免此类 latch 的方法主要有 2 种,一种是补全 if-else 结构,或者对信号赋初值。
例如,上面模型中的always语句,可以改为以下两种形式:
// 补全条件分支结构
always @(*) begin
if (en) q = data ;
else q = 1'b0 ;
end
//赋初值
always @(*) begin
q = 1'b0 ;
if (en) q = data ; //如果en有效,改写q的值,否则q会保持为0
end
但是在时序逻辑中,不完整的 if - else 结构,不会产生 latch,例如下面模型。
这是因为,q 寄存器具有存储功能,且其值在时钟的边沿下才会改变,这正是触发器的特性。
module module1_ff(
input clk ,
input data,
input en ,
output reg q) ;
always @(posedge clk) begin
if (en) q <= data ;
end
endmodule
在组合逻辑中,当条件语句中有很多条赋值语句时,每个分支条件下赋值语句的不完整也是会产生 latch。
其实对每个信号的逻辑拆分来看,这也相当于是 if-else 结构不完整,相关寄存器信号缺少在其他条件下的赋值行为。例如:
module module1_latch11(
input data1,
input data2,
input en ,
output reg q1 ,
output reg q2) ;
always @(*) begin
if (en) q1 = data1 ;
else q2 = data2 ;
end
endmodule
这种情况也可以通过补充完整赋值语句或赋初值来避免 latch。例如:
always @(*) begin
//q1 = 0; q2 = 0 ; //或在这里对 q1/q2 赋初值
if (en) begin
q1 = data1 ;
q2 = 1'b0 ;
end
else begin
q1 = 1'b0 ;
q2 = data2 ;
end
end
case 结构不完整
case 语句产生 Latch 的原理几乎和 if 语句一致。在组合逻辑中,当 case 选项列表不全且没有加 default 关键字,或有多个赋值语句不完整时,也会产生 Latch。例如:
module module1_latch2(
input data1,
input data2,
input [1:0] sel ,
output reg q ) ;
always @(*) begin
case(sel)
2'b00: q = data1 ;
2'b01: q = data2 ;
endcase
end
endmodule
当然,消除此种 latch 的方法也是 2 种,将 case 选项列表补充完整,或对信号赋初值。
补充完整 case 选项列表时,可以罗列所有的选项结果,也可以用 default 关键字来代替其他选项结果。
例如,上述 always 语句有以下 2 种修改方式。
always @(*) begin
case(sel)
2'b00: q = data1 ;
2'b01: q = data2 ;
default: q = 1'b0 ;
endcase
end
always @(*) begin
case(sel)
2'b00: q = data1 ;
2'b01: q = data2 ;
2'b10, 2'b11 :
q = 1'b0 ;
endcase
end
原信号赋值或判断
在组合逻辑中,如果一个信号的赋值源头有其信号本身,或者判断条件中有其信号本身的逻辑,则也会产生 latch。因为此时信号也需要具有存储功能,但是没有时钟驱动。此类问题在 if 语句、case 语句、问号表达式中都可能出现,例如:
//signal itself as a part of condition
reg a, b ;
always @(*) begin
if (a & b) a = 1'b1 ; //a -> latch
else a = 1'b0 ;
end
//signal itself are the assigment source
reg c;
wire [1:0] sel ;
always @(*) begin
case(sel)
2'b00: c = c ; //c -> latch
2'b01: c = 1'b1 ;
default: c = 1'b0 ;
endcase
end
//signal itself as a part of condition in "? expression"
wire d, sel2;
assign d = (sel2 && d) ? 1'b0 : 1'b1 ; //d -> latch
避免此类 Latch 的方法,就只有一种,即在组合逻辑中避免这种写法,信号不要给信号自己赋值,且不要用赋值信号本身参与判断条件逻辑。
例如,如果不要求立刻输出,可以将信号进行一个时钟周期的延时再进行相关逻辑的组合。上述第一个产生 Latch 的代码可以描述为:
reg a, b ;
reg a_r ;
always (@posedge clk)
a_r <= a ;
always @(*) begin
if (a_r & b) a = 1'b1 ; //there is no latch
else a = 1'b0 ;
end
敏感信号列表不完整
如果组合逻辑中 always@() 块内敏感列表没有列全,该触发的时候没有触发,那么相关寄存器还是会保存之前的输出结果,因而会生成锁存器。
这种情况,把敏感信号补全或者直接用 always@(*) 即可消除 latch。
小结
总之,为避免 latch 的产生,在组合逻辑中,需要注意以下几点:
1)if-else 或 case 语句,结构一定要完整
2)不要将赋值信号放在赋值源头,或条件判断中
3)敏感信号列表建议多用 always@(*)
6.3 Verilog 书写规范
在编程时多注意以下几点,也可以避免大多数的竞争与冒险问题。
- 1)时序电路建模时,用非阻塞赋值。
- 2)组合逻辑建模时,用阻塞赋值。
- 3)在同一个 always 块中建立时序和组合逻辑模型时,用非阻塞赋值。
- 4)在同一个 always 块中不要既使用阻塞赋值又使用非阻塞赋值。
- 5)不要在多个 always 块中为同一个变量赋值。
- 6)避免 latch 产生。
下面,对以上事项逐条分析。
1)时序电路建模时,用非阻塞赋值
前面讲述非阻塞赋值时就陈述过,时序电路中非阻塞赋值可以消除竞争冒险。
例如下面代码描述,由于无法确定 a 与 b 阻塞赋值的操作顺序,就有可能带来竞争冒险。
always @(posedge clk) begin
a = b ;
b = a ;
end
而使用非阻塞赋值时,赋值操作是同时进行的,所以就不会带来竞争冒险,如以下代码描述。
always @(posedge clk) begin
a <= b ;
b <= a ;
end
2)组合逻辑建模时,用阻塞赋值
例如,我们想实现 C = A&B, F=C&D 的组合逻辑功能,用非阻塞赋值语句如下。
两条赋值语句同时赋值,F <= C & D 中使用的是信号 C 的旧值,所以导致此时的逻辑是错误的,F 的逻辑值不等于 A&B&D。
而且,此时要求信号 C 具有存储功能,但不是时钟驱动,所以 C 可能会被综合成锁存器(latch),导致竞争冒险。
always @(*) begin
C <= A & B ;
F <= C & D ;
end
对代码进行如下修改,F = C & D 的操作一定是在 C = A & B 之后,此时 F 的逻辑值等于 A&B&D,符合设计。
always @(*) begin
C = A & B ;
F = C & D ;
end
3)在同一个 always 块中建立时序和组合逻辑模型时,用非阻塞赋值
虽然时序电路中可能涉及组合逻辑,但是如果赋值操作使用非阻塞赋值,仍然会导致如规范 1 中所涉及的类似问题。
例如在时钟驱动下完成一个与门的逻辑功能,代码参考如下。
always @(posedge clk or negedge rst_n)
if (!rst_n) begin
q <= 1'b0;
end
else begin
q <= a & b; //即便有组合逻辑,也不要写成:q = a & b
end
end
4)在同一个 always 块中不要既使用阻塞赋值又使用非阻塞赋值
always 涉及的组合逻辑中,既有阻塞赋值又有非阻塞赋值时,会导致意外的结果,例如下面代码描述。
此时信号 C 阻塞赋值完毕以后,信号 F 才会被非阻塞赋值,仿真结果可能正确。
但如果 F 信号有其他的负载,F 的最新值并不能马上传递出去,数据有效时间还是在下一个触发时刻。此时要求 F 具有存储功能,可能会被综合成 latch,导致竞争冒险。
always @(*) begin
C = A & B ;
F <= C & D ;
end
如下代码描述,仿真角度看,信号 C 被非阻塞赋值,下一个触发时刻才会有效。而 F = C & D 虽然是阻塞赋值,但是信号 C 不是阻塞赋值,所以 F 逻辑中使用的还是 C 的旧值。
always @(*) begin
C <= A & B ;
F = C & D ;
end
下面分析假如在时序电路里既有阻塞赋值,又有非阻塞赋值会怎样,代码如下。
假如复位端与时钟同步,那么由于复位导致的信号 q 为 0,是在下一个时钟周期才有效。
而如果是信号 a 或 b 导致的 q 为 0,则在当期时钟周期内有效。
如果 q 还有其他负载,就会导致 q 的时序特别混乱,显然不符合设计需求。
always @(posedge clk or negedge rst_n)
if (!rst_n) begin //假设复位与时钟同步
q <= 1'b0;
end
else begin
q = a & b;
end
end
需要说明的是,很多编译器都支持这么写,上述的分析也都是建立在仿真角度上。实际中如果阻塞赋值和非阻塞赋值混合编写,综合后的电路时序将是错乱的,不利于分析调试。
5)不要在多个 always 块中为同一个变量赋值
与 C 语言有所不同,Verilog 中不允许在多个 always 块中为同一个变量赋值。此时信号拥有多驱动端(Multiple Driver),是禁止的。当然,也不允许 assign 语句为同一个变量进行多次连线赋值。 从信号角度来讲,多驱动时,同一个信号变量在很短的时间内进行多次不同的赋值结果,就有可能产生竞争冒险。
从语法来讲,很多编译器检测到多驱动时,也会报 Error。