力扣刷题篇之数与位2

系列文章目录

---

目录

系列文章目录

前言

数值计算

总结

---

前言

 本系列是个人力扣刷题汇总，本文是数与位。刷题顺序按照[力扣刷题攻略] Re：从零开始的力扣刷题生活 - 力扣（LeetCode）

 

数值计算

415. 字符串相加 - 力扣（LeetCode）

class Solution {
    public String addStrings(String num1, String num2) {
        StringBuilder sb = new StringBuilder();
        int carry = 0, i = num1.length()-1, j = num2.length()-1;
        while(i >= 0 || j >= 0 || carry != 0){
            if(i>=0) carry += num1.charAt(i--)-'0';
            if(j>=0) carry += num2.charAt(j--)-'0';
            sb.append(carry%10);
            carry /= 10;
        }
        return sb.reverse().toString();
    }
}

43. 字符串相乘 - 力扣（LeetCode）

class Solution {
    public String multiply(String num1, String num2) {
        int len1 = num1.length(),len2 = num2.length();
        if (len1 == 1 && num1.charAt(0) - '0' == 0
                || len2 == 1 && num2.charAt(0) - '0' == 0) {
            return "0";
        }
        int [] sums = new int [len1+len2];
        int [] nums1 = new int [len1];
        for (int i = 0; i < len1; i++) {
            nums1[i] = num1.charAt(i) - '0';
        }
        for(int i=0;i=10){
                sums[i+1] +=sums[i]/10;
                sums[i]%=10;
            }
            if(i==sums.length-1&&sums[i]==0)
                continue;
            str.append(sums[i]);
        }
        return str.reverse().toString();
    }
}

 

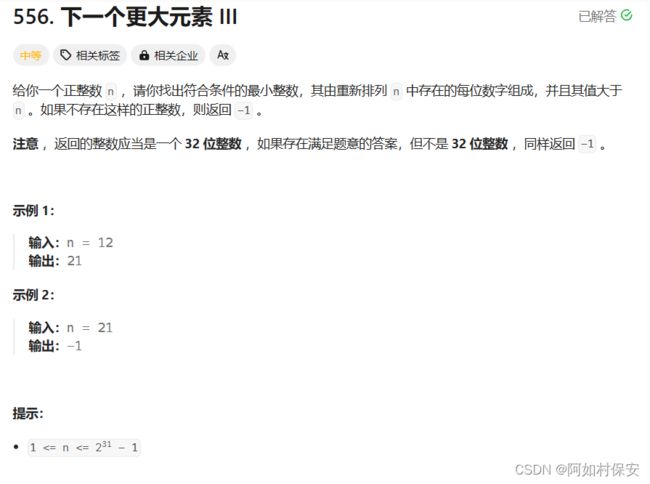
使用了一个链表来存储整数的每一位，并在这个链表上进行操作。整体思路是从后往前找到第一个递增的位置 i，然后在 [i+1, t.size()-1] 范围内找到比 i 位置大的最小的数，与 i 位置交换，再调整 [i+1, t.size()-1] 的顺序，最后检查是否越界。如果不越界，返回调整后的整数，否则返回 -1。 

class Solution {
    public int nextGreaterElement(int n) {
        if(n == Integer.MAX_VALUE) return -1;
        LinkedList t = new LinkedList<>();
        while (n != 0) {
            t.addFirst(n % 10);
            n = n / 10;
        }

        for (int i = t.size() - 2; i >= 0; --i) {
            if (t.get(i) < t.get(i + 1)) {
                //调整i位置即可
                //向后找比i大的 最小的数的位置 交换
                int targetIndex = i + 1;
                for (int j = i + 1; j < t.size(); ++j) {
                    if (t.get(j) > t.get(i) && t.get(j) <= t.get(targetIndex)) {
                        targetIndex = j;
                    }
                }
                swap(t, i, targetIndex);

                //调整从i+1开始到结尾的顺序 [i+1,t.size()-1] 依次递增 保证最小
                int l =i+1,r=t.size()-1;
                while(lInteger.MAX_VALUE) return -1;
            
                return (int)res;

            }
        }

        return -1;
    }

    private void swap(LinkedList t, int a, int b) {
        int tmp = t.get(a);
        t.set(a, t.get(b));
        t.set(b, tmp);
    }
}

9. 回文数 - 力扣（LeetCode）

 通过反转整数的一半来判断是否为回文数。在反转的过程中，如果反转的数字大于剩余的数字，就可以停止，因为已经检查过一半了。最后，比较原始数字和反转后的数字，如果相等，或者相等除以 10（对于偶数位数的数字），则是回文数。此解法的时间复杂度为 O(log n)。

class Solution {
    public boolean isPalindrome(int x) {
        // 负数和以0结尾但不是0的数不是回文数
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int revertedNumber = 0;
        // 反转 x 的一半数字
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }
        // 对于奇数位数的数字，revertedNumber 的最后一位是中间位，不影响回文判断
        // 对于偶数位数的数字，x 和 revertedNumber 必须完全相等
        return x == revertedNumber || x == revertedNumber / 10;
    }
}

使用了递归的思想。如果一个数字大于等于 10，就继续将其各个位数相加，直到得到一个一位数为止。递归函数的返回值即为最终的结果。 

class Solution {
    public int addDigits(int num) {
        if (num < 10) {
            return num;
        }
   
       return addDigits(num / 10+ num % 10);
    }
}

461. 汉明距离 - 力扣（LeetCode）

 首先计算了两个整数的异或结果，然后遍历这个异或结果的每一位，通过与 1 进行位与操作统计不同位的数量。

class Solution {
    public int hammingDistance(int x, int y) {
        //  0 0 0 1 (1)
        //  0 1 0 0 (4)

        //^ 0 1 0 1 (5)
        //& 0 0 0 1 (1)
        //   ------
        //  0 0 0 1   (结果)

        int t = x ^ y;
        int count = 0;
        while(t != 0) {
            // 将 num 与 1 进行位与操作，统计最低位是否为1
            count += (t & 1);
            // // 将 num 右移一位
            t = t >> 1;
        }
        return count;
    }
}

477. 汉明距离总和 - 力扣（LeetCode）

使用了位运算。对于每个二进制位，它统计在该位上为 1 的元素个数 n，然后计算当前位上的汉明距离，并将其累加到结果中。最终返回总的汉明距离。这种方法的时间复杂度是 O(32n)，可以在线性时间内完成计算。 

class Solution {
    public int totalHammingDistance(int[] nums) {
        int res = 0;
        int m = nums.length;

        // 遍历每个二进制位（最多 30 位）
        for (int i = 0; i <= 30; i++) {
            int n = 0;

            // 统计在当前位上为1的元素个数
            for (int num : nums) {
                n += (num >>> i) & 1;
            }

            // 计算当前位上的汉明距离，并累加到结果中
            res += (m - n) * n;
        }
        return res;
    }
}

---

总结

把数与位的第二部分数值计算写完了，好简单！（最后这个累加汉明距离的要记牢。）我好爱哈哈哈哈，继续加油，多敲多敲，我要找实习了。