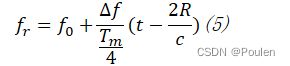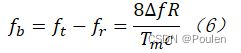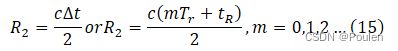雷达测距原理、精度、分辨力以及最大不模糊距离知识汇总

基础知识

• 电磁波在空间中通常是以恒定的速度沿直线传播的，但会因大气和气候条件的改变而略有不同
• 电磁波在空气中以接近光的速度传播
• 电磁波的反射现象，当电磁波遇到障碍物会被反射

• 雷达的工作原理与声波反射原理非常相似。如果我们朝着岩石峡谷或洞穴方向大喊大叫，我们将听到回声。当我们知道空气中的声速，就可以估计物体的距离和大致方向。

1.测距原理

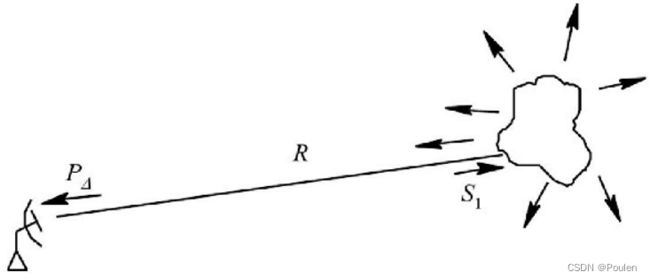
        测量目标的距离是雷达的基本任务之一。无线电波在均匀介质中以固定的速度直线传播(在自由空间传播速度约等于光速c=3×105km/s)。如下图所示。目标至雷达的斜距R可以通过测量电磁波在雷达和目标之间往返一次所需的时间得到，即：

而时间也就是回波相对发射信号的延迟，因此，目标距离测量就是要精确测定延迟时间。然而根据雷达发射信号的不同，测定延迟时间通常可以采用脉冲法、频率法和相位法。通常延迟时间的测定脉冲雷达采用脉冲法，连续波雷达采用频率法或相位法。

1.1脉冲法测距(显示器上测距)

1.1.1 基本原理

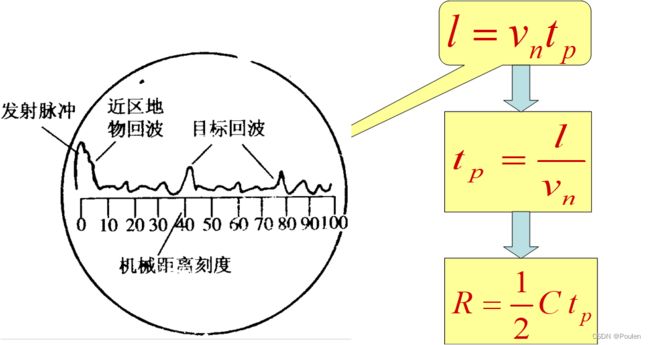
        在常用的脉冲雷达中, 回波信号是滞后于发射脉冲的回波脉冲。在荧光屏上目标回波出现的时刻滞后于主波, 滞后的时间就是tR, 测量距离就是要测出时间。说白了脉冲测量的本质就是测量发射脉冲跟和回波之间的时延来估计目标距离，早期雷达均用显示器作为终端，在显示器画面上根据扫掠量程和回波位置直接测读延迟时间。现代雷达常常采用电子设备自动地测读回波到达的迟延时间tR。

1.在显示器上测距

2.确定回波到达位置

        有两种定义回波到达时间的方法：一种是以目标回波脉冲的前沿作为它的到达时刻；另一种是以回波脉冲的中心(或最大值)作为它的到达时刻。对于通常碰到的点目标来讲，两种定义所得的距离数据只相差一个固定值(约为2)，可以通过距离校零予以消除。用脉冲前沿作为到达时刻的缺点是容易受回波大小及噪声的影响, 比较电平不稳也会引起误差。

1.2 调频法测距

1.2.1 调频法测距原理

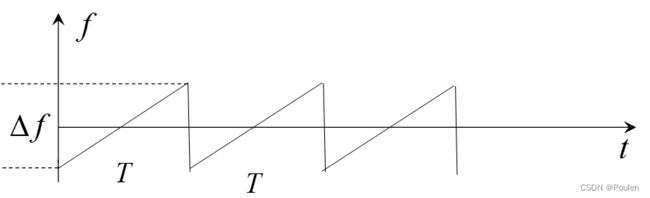
        调频法测距可以用在连续波雷达，也可以用在脉冲雷达。连续发射的信号具有频率调制的标志后就可以测定目标的距离。在高重复频率的脉冲雷达中，发射脉冲频率有规律的调制就提供了解模糊的可能性。对载频进行频率调制是用得很广的展宽连续波雷达频谱的一种技术，定时标志就是变化着的频率。如下图。发射机产生连续高频等幅波, 其频率在时间上按三角形规律或按正弦规律变化, 目标回波和发射机直接耦合过来的信号加到接收机混频器内。

         在无线电波传播到目标并返回天线的这段时间内, 发射机频率较之回波频率已有了变化, 因此在混频器输出端便出现了差频电压。差频电压经放大、限幅后加到频率计上。由于差频电压的频率与目标距离有关，因而频率计上的刻度可以直接采用距离长度作为单位。

        调频连续波(FMCW: Frequency Modulation Continuous Wave)雷达的发射频率按已知的时间函数变化，它利用在时间上改变发射信号的频率并测量接收信号频率的方法来测定目标距离。在任何给定瞬间，发射频率与接收频率的相关不仅是测量目标距离的尺度，而且还是测量目标径向速度的尺度。由于任何实际的连续波雷达频率不可能向一个方向连续变化，所以必须采用周期性的调制。

调制波形通常有：

锯齿波、三角波、正弦波、步进频率

线性调频：

目标回波延迟时间正比于回波信号和发射信号的频率差。

在给定的时间范围内发射的频率偏移越大，测量延迟时间的分辨力就越高，发射频谱也越宽。

1.2.1.1 锯齿波调频

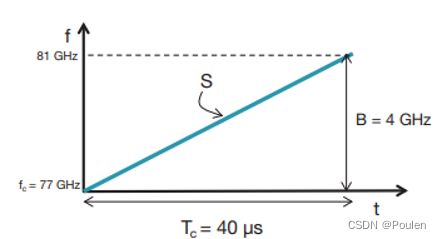
如上图所示，锯齿波调频是指发射信号频率按锯齿波形周期变化。在一个周期内发射信号频率线性变化，称为线性调频LFM，又称Chirp信号。以下是锯齿波调频测距原理的介绍：

上图为一个Chirp频率随时间变化图。假设该线性调频脉冲具有起始频率（fc）,带宽（B）和持续时间（Tc）。该线性调频脉冲的斜率（S）捕获频率的变化率。

雷达发射天线发射Chirp信号，经过时间τ后，接收天线收到目标反射回来的信号，其频率差为τ（对于与雷达无径向运动的目标(fd=0)而言，其回波信号与发射信号的频率差就决定于其回波延迟，因此测频差就可确定目标回波时延，即测距。）,即可得到中频0

 由（1）可得最终目标的距离R为：

1.2.1.2 三角波调频 

         将频率按周期三角变化规律的信号通过天线发射，其平均频率为0，频率变化的周期为，最大频偏为∆。将t时刻的发射频率记作，则有：

该三角调频信号遇到目标后产生回波，回波信号通过天线返回到接收机。回波频率和发射频率的变化规律相同，但在时间上滞后，滞后的时间与雷达和目标的距离有关，将雷达和目标的距离记为R,则滞后时间=2,将回波频率记作,可得：

发射频率和回波频率间的差拍频率为：

由此可得目标距离为：

是三角调频的频率，不是发射信号的频率。 

总结：调频法测距的关键就是获得发射信号和接收信号的差频(中频)，然后根据该频率获得距离 

2.影响测距精度的因素 

         雷达在测量量目标距离时，不可避免地产生误差。由测距公式可以看出影响测距精度的因素。对测距公式进行全微分，得到

用增量代替微分，可得到测距误差为

式中，∆为电波传播速度平均值误差；∆为测量目标回波延迟时间的误差。由该式可以看出，测距误差由电波传播速度c的变化∆以及测时误差∆两部分组成。

误差按性质可分为系统误差和随机误差两类。

        系统误差是指在测距时, 系统各部分对信号的固定延时所造成的误差, 系统误差以多次测量的平均值与被测距离真实值之差来表示。从理论上讲, 系统误差在校准雷达时可以补偿掉, 实际工作中很难完善地补偿 , 因此在雷达的技术参数中, 常给出允许的系统误差范围。

        随机误差系指因某种偶然因素引起的测距误差, 所以又称偶然误差。凡属设备本身工作不稳定性造成的随机误差称为设备误差, 如接收时间滞后的不稳定性、各部分回路参数偶然变化、晶体振荡器频率不稳定以及读数误差等。凡属系统以外的各种偶然因素引起的误差称为外界误差, 如电波传播速度的偶然变化、电波在大气中传播时产生折射以及目标反射中心的随机变化等。

        随机误差一般不能补偿掉, 因为它在多次测量中所得的距离值不是固定的而是随机的。因此, 随机误差是衡量测距精度的主要指标。

2.1电磁波传播速度变化产生的误差

        实际上大气层的分布是不均匀的且其参数随时间、地点而变化。大气密度、湿度、 温度等参数的随机变化, 导致大气传播介质的导磁系数和介电常数也发生相应的改变, 因而电波传播速度c不是常量而是一个随机变量。由式(8)可知, 由于电波传播速度的随机误差而引起的相对测距误差为

在昼夜间大气中温度、气压及湿度的起伏变化所引起的传播速度变化为Δc/c≈10-5, 例如R=60 km时, ΔR=60×103×10-5=0.6m的数量级,对常规雷达来讲可以忽略。电波在大气中的平均传播速度和光速亦稍有差别, 且随工作波长λ而异, 因而在测距公式(1)中的c值亦应根据实际情况校准, 否则会引起系统误差, 表1列出了几组实测的电波传播速度值。

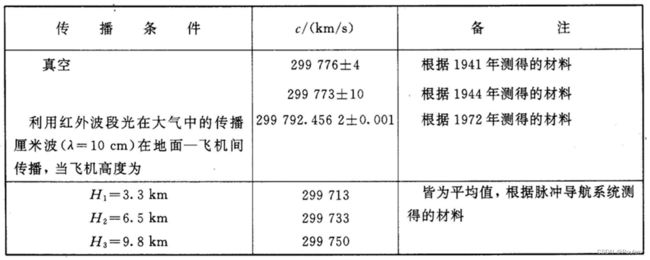表 1 在不同条件下电磁波传播速度

 因此根据雷达工作环境适当调整电磁波传播速度可以减少电磁波传播速度变化产生的误差。

2.2 因大气折射引起的误差

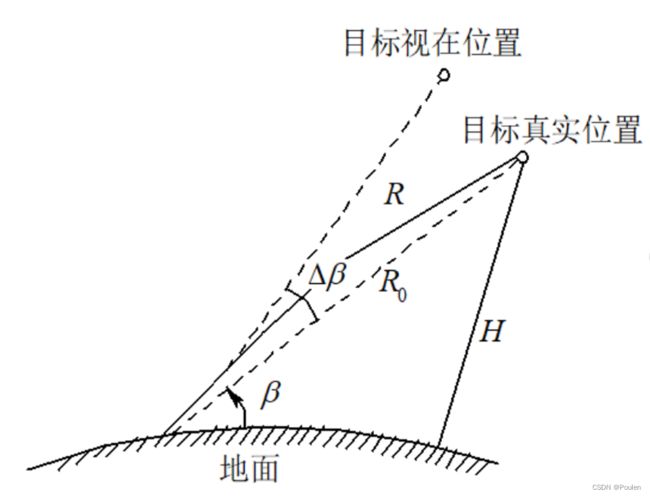
        当电波在大气中传播时, 由于大气介质分布不均匀将造成电波折射, 因此电波传播的路径不是直线而是走过一个弯曲的轨迹。在正折射时电波传播途径为一向下弯曲的弧线。由图可看出, 虽然目标的真实距离是R0, 但因电波传播不是直线而是弯曲弧线, 故所测得的回波延迟时间tR=2R/c,这就产生一个测距误差(同时还有测仰角的误差Δβ): 

由式(10)可知∆大小和大气层对电磁波的折射率有直接关系。如果知道了折射率和高度关系，就可以计算出不同高度和距离的目标由于大气折射所产生的距离误差，从而给测量值以必要的修正。当目标距离越远、高度越高时，由折射所引起的测距误差∆也越大。例如在一般大气条件下，当目标距离为100km，仰角0.1rad时，距离误差为16m的量级。

2.3测读方法误差 

        测距所用具体方法不同, 其测距误差亦有差别。早期的脉冲雷达直接从显示器上测量目标距离, 这时显示器荧光屏亮点的直径大小、所用机械或电刻度的精度、人工测读时的惯性等都将引起测距误差。当采用电子自动测距的方法时, 如果测读回波脉冲中心, 则回波中心的估计误差(正比于脉宽τ而反比于信噪比)以及计数器的量化误差等均将造成测距误差。

2.4 总结

        总而言之，雷达测距精度就是雷达测距值与目标实际值之间的差值，该值越小，测距精度越高，通常使用均方误差来衡量。一般的影响测距精度误差的主要因素有电磁波传播速度变化、大气折射以及测读方法。此外测距精度误差按照性质分为系统误差和随机误差，通常系统误差是可以被校准，而随机误差是不能校准的，并且随机误差是衡量测距精度的主要指标。

3.距离分辨率和测距范围

3.1距离分辨率

        距离分辨力是指同一方向上两个大小相等点目标之间最小可区分距离。在显示器上测距时(即脉冲法测距), 分辨力主要取决于回波的脉冲宽度τ, 同时也和光点直径d所代表的距离有关。定义距离分辨力Δrc为

式中, d为光点直径; υn为光点扫掠速度(cm/μs)。

用电子方法测距或自动测距时，距离分辨率由脉冲宽度τ或波门宽度决定，脉冲宽度越窄，距离分辨率越好。对于复杂的脉冲压缩信号，决定距离分辨率的是雷达信号的有效带宽B,有效带宽越宽，距离分辨力越好。距离分辨率可表示为： 

注意：信号只要具有大的持续带宽就能获得很高的距离分辨率，而不必具有很窄的脉冲宽度。(信号持续带宽定义为信号时延分辨常数的倒数，而时延分辨常数由模糊函数确定)

3.2 测距范围 

        测距范围包括最小可测距离和最大单值测距范围。

        最小可测距离，是指雷达能测量的最近目标的距离。脉冲雷达使用收发共用天线，在发射脉冲带宽τ时间内，接收机和天线馈线系统间是“断开”的，不能正常接收目标回波，发射脉冲过去后天线收发开关恢复到接收状态，也需要一段时间0,在这段时间内，由于不能正常接收回波信号，雷达是很难进行测距的。因此，雷达的最小可测距离为：

        雷达的最大单值测距范围(最大不模糊距离)由其脉冲重复周期决定。为了保证单值测距，通常应选取

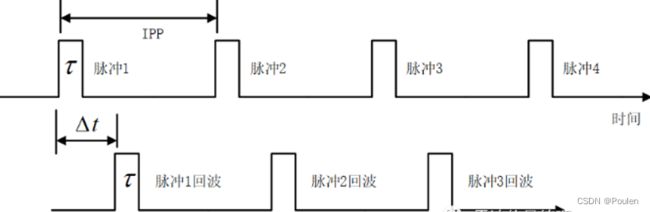
式中表示雷达最大作用距离，由雷达方程决定。有时雷达重复频率的选择不能满足单值测距的要求，将产生测距模糊(距离模糊)，距离模糊产生过程如下图所示：

当往返时间∆==对应的距离被称为雷达的最大不模糊距离。回波1表示脉冲1从距离雷达R1=c∆的目标产生的雷达回波。回波2可以解释为脉冲2从相同目标产生的回波，也可以解释为脉冲1从距离雷达为R2的目标产生的回波。即

很显然回波2带有距离模糊。因此，雷达发射了脉冲就必须等待足够长的时间再发射下一次脉冲，以便在下一次脉冲发射前接收到最远距离的目标回波。因此雷达最大不模糊距离对应于脉冲重复频率的一半：

如果在设计雷达系统时，雷达重复频率的选择不能满足单值测距的要求，产生距离模糊，有上述可知，这是目标回波对应的距离R为：

式中，为测得的回波信号与发射脉冲间的时延。为了得到目标的真实距离R,必须通过一些方法判明式（17）中的模糊值m。当雷达脉冲重复间隔不满足(14)时将会产生距离模糊，为了解决距离模糊问题,下面讨论多种重复频率和“舍脉冲”两种距离模糊消除方法。

3.2.1 多种重复频率（多重频技术）

         设重复频率分别为1和2（脉冲重复周期为1和2，且1<2,1>2），对应的不模糊距离分别为1=21和1=22，并且小于期望的不模糊距离（可以认为是一定工作模式下的最大不模糊距离），对应的PRF为,=2。

1和2的选择应保证在一个期望的脉冲重复周期PRI(Td=1/frd)内，两种PRF下发射的脉冲数目互质，如选取：1=∗、2=+1∗。在一个期望的脉冲重复周期内，两种发射信号的回波仅在一个时延位置上重合，这就是真正的目标位置。设M1和M2分别为雷达在一个期望的PRI内两种PRF下对应的脉冲数。在一个期望的脉冲重复周期内，有M1=M2=M或M1+1=M2,只需测出两种回波信号对应的时延t1和t2（为相对于当前发射脉冲的时延），根据下面三种情况，即可求出目标的距离。 

  

因此，只要得到这两种PRF可能模糊的时延t1和t2，就可以计算得到目标实际的距离。 

 3.2.2 “舍脉冲”法

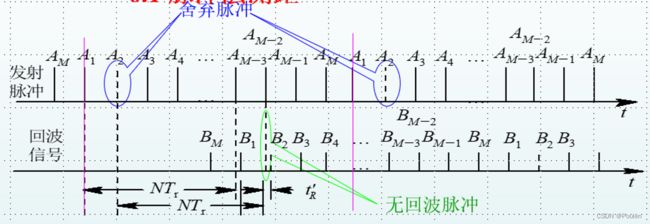
         所谓“舍脉冲”, 就是在每发射M个脉冲中舍弃一个, 作为发射脉冲串的附加标志。如下图所示。

发射脉冲从A1到AM, 其中A2不发射。与发射脉冲相对应, 接收到的回波脉冲串同样是每M个回波脉冲中缺少一个。只要从A2以后, 逐个累计发射脉冲数, 直到某一发射脉冲(在图中是AM-2)后没有回波脉冲(如图中缺B2)时停止计数, 则累计的数值就是回波跨越的重复周期数m。 知道m之后就可套用(11)解距离模糊。