数据结构算法——二分查找问题（以LeetCode二分查找题为例）
1. 二分查找
1.1 二分查找的定义
二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法，前提是数据结构必须先排好序。
二分查找采用的是一种分治策略，它充分利用了元素间的次序关系，可在最坏的情况下用O(log n)完成搜索任务。
1.2 二分查找基本思想
假设数组元素呈升序排列，将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的x作比较，如果x=a[n/2]则找到x，算法终止；如 果x
1.3 二分查找流程图
1.4 二分查找优缺点
优点：比较次数少，查找速度快，平均性能好；
缺点：要求待查表为有序表，且插入删除困难。
因此，二分查找方法适用于不经常变动而查找频繁的有序列表。使用条件：查找序列是顺序结构，有序。
2. 二分查找的实现
以对int数组进行二分查找为例
2.1 非递归实现
public class BinarySearch {
public int binarySearch(int nums[], int key) {
int low = 0, high = nums.length - 1, mid = 0;
if (key < nums[low] || key > nums[high]) {
return -1;
}
while (low <= high) {
mid = (low + high) / 2;
if (nums[mid] == key) {
return mid;
} else if (nums[mid] > key) {
high = mid - 1;
} else {
low = mid + 1;
}
}
//未找到
return -1;
}
public static void main(String[] args) {
int[] nums = {1, 2, 3, 4, 5, 6, 7, 8, 9};
BinarySearch binarySearch = new BinarySearch();
int res = binarySearch.binarySearch(nums, 6);
System.out.println(res);
}
}
2.2 递归实现
public class BinarySearchRecursive {
public int binarySearch(int nums[], int key,int low,int high) {
if(low > high || key < nums[low] || key > nums[high]){
return -1;
}
int mid = (low+high)/2;
if(nums[mid]==key){
return mid;
}else if (nums[mid]>key){
return binarySearch(nums,key,low,mid-1);
}else {
return binarySearch(nums,key,low+1,high);
}
}
public static void main(String[] args) {
int[] nums = {1, 2, 3, 4, 5, 6, 7, 8, 9};
BinarySearchRecursive binarySearch = new BinarySearchRecursive();
int res = binarySearch.binarySearch(nums, 6,0,nums.length-1);
System.out.println(res);
}
}
3. 搜索二维矩阵
力扣
https://leetcode.cn/problems/search-a-2d-matrix/
3.1 题目描述
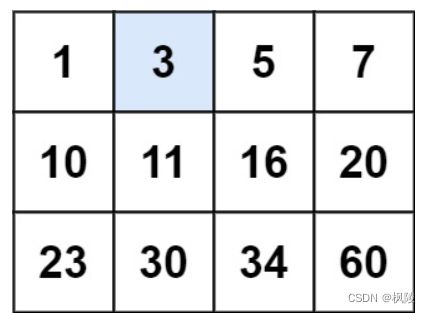
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例：
输入： matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出： true
3.2 解决方法
3.2.1 二分查找
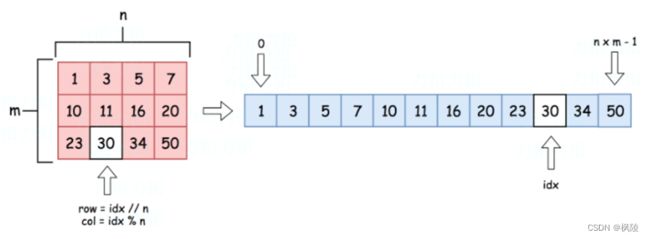
这是一个元素查找问题，且元素按序排列，自然可用二分查找。可将二维矩阵延展开来，视为一个有序的数组。
行列坐标为(row, col)的元素，展开之后索引下标为idx = row * n + col；反过来，对于一维下标为idx的元素，对应二维数组中的坐标就应该是：row = idx / n; col = idx % n
public class SearchMatrix {
public boolean searchMatrix(int[][] matrix, int target){
int m = matrix.length;
int n = matrix[0].length;
if(m == 0 || n == 0){
return false;
}
int low = 0, high = m*n-1;
while (low <= high){
int mid = (high+low)/2;
int midNum = matrix[mid/n][mid%n];
if(midNum == target){
return true;
}else if(midNum > target){
high = mid-1;
}else {
low = mid+1;
}
}
return false;
}
public static void main(String[] args) {
int[][] matrix = {{1,3,5,7},{10,11,16,20},{23,30,34,50}};
SearchMatrix searchMatrix = new SearchMatrix();
System.out.println(searchMatrix.searchMatrix(matrix, 3));
}
}
复杂度分析
时间复杂度 : 由于是标准的二分查找，时间复杂度为O(log(m n))。
空间复杂度 : 没有用到额外的空间，复杂度为O(1)。
4. 寻找重复数
力扣https://leetcode.cn/problems/find-the-duplicate-number/
4.1 题目描述
给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例：
输入： nums = [1,3,4,2,2]
输出： 2
4.2 解决方法
怎样证明nums中存在至少一个重复值？其实很简单，这是“抽屉原理”（或者叫“鸽子洞原理”）的简单应用。
nums 中的每个数字（n+1个）都是一个物品，nums中可以出现的每个不同的数字（n个）都是一个 “抽屉”。把n+1 个物品放入n个抽屉中，必然至少会有一个抽屉放了2个或者2个以上的物品。所以这意味着nums中至少有一个数是重复的。
4.2.1 二分查找
根据抽屉原理肯定会有重复数。对于增加重复数的方式，整体应该有两种可能：
1. 如果重复数（比如叫做target）只出现两次，那么其实就是1~N所有数都出现了一次，然后再加一个target；
2. 如果重复数target出现多次，那在情况1的基础上，它每多出现一次，就会导致1~N中的其它数少一个。
我们可以发现一个规律：
1. 以target为界，对于比target小的数i，数组中所有小于等于它的数，最多出现一次（有可能被多出现的target占用了），所以总个数不会超过i。
2. 对于比target大的数j，如果每个元素都只出现一次，那么所有小于等于它的元素是j个；而现在target会重复出现，所以总数一定会大于j。
所以要找target，其实就是要找1~N中这个分界的数。所以我们可以对1~N的N个自然数进行二分查找，它们可以看作一个排好序的数组，但不占用额外的空间。
public class FindDuplicate1 {
public int findDuplicate(int[] nums){
int low = 1;
int high = nums.length-1;
while (low <= high){
int mid = (high+low)/2;
int count = 0;
for (int j =0; j
复杂度分析
时间复杂度：O(nlog n)，其中 n 为nums[] 数组的长度。二分查找最多需要O(logn) 次，而每次判断count的时候需要O(n) 遍历 nums[] 数组求解小于等于 i 的数的个数，因此总时间复杂度为O(nlogn)。
空间复杂度：O(1)。我们只需要常数空间存放若干变量。
4.2.2 快慢指针法（循环检测）
把nums看成是顺序存储的链表，nums中每个元素的值是下一个链表节点的地址。那么如果nums有重复值，说明链表存在环，本问题就转化为了找链表中环的入口节点，因此可以用快慢指针解决。
整体思路如下：
第一阶段，寻找环中的节点
1. 初始时，都指向链表第一个节点nums[0]；
2. 慢指针每次走一步，快指针走两步；
3. 如果有环，那么快指针一定会再次追上慢指针；相遇时，相遇节点必在环中
第二阶段，寻找环的入口节点（重复的地址值）
4. 重新定义两个指针，让before，after分别指向链表开始节点，相遇节点
5. before与after相遇时，相遇点就是环的入口节点
综上：从环外0开始，和从相遇点开始，走同样多的步数之后，一定可以在入口处相遇。所以第二阶段的相遇点，就是环的入口，也就是重复的元素。
public class FindDuplicate2 {
public int findDuplicate(int[] nums) {
int slow = 0, fast = 0;
do {
slow = nums[slow];
fast = nums[nums[fast]];
} while (slow != fast);
int before = 0, after = slow;
while (before != after) {
before = nums[before];
after = nums[after];
}
return before;
}
public static void main(String[] args) {
int[] nums = {1, 3, 4, 2, 2};
FindDuplicate2 findDuplicate = new FindDuplicate2();
System.out.println(findDuplicate.findDuplicate(nums));
}
}
复杂度分析
时间复杂度：O(n)，不管是寻找环上的相遇点，还是环的入口，访问次数都不会超过数组长度。
空间复杂度：O(1)，我们只需要定义几个指针就可以了。