LeetCode刷题复盘笔记—669. 修剪二叉搜索树

今日主要总结一下，669. 修剪二叉搜索树

题目：669. 修剪二叉搜索树

Leetcode题目地址

题目描述：
给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

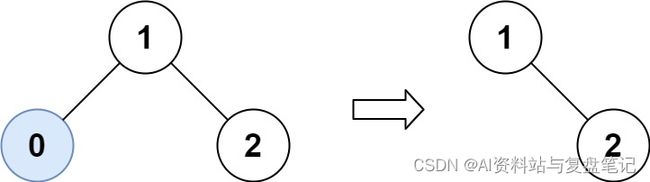
示例 1：

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]
示例 2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 104] 内
0 <= Node.val <= 104
树中每个节点的值都是 唯一 的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104

本题重难点

做这道题之前最好，做一下Leetcode701.二叉搜索树中的插入操作和Leetcode450. 删除二叉搜索树中的节点两道题，也可以直接看一下我上一篇文章的讲解：一文搞懂怎么删除二叉搜索树和普通二叉树节点
这道题会理解得更加清晰透彻！

这道题，如果初步想，可能会存在一些误区，直接想法就是：递归处理，然后遇到 root->val < low || root->val > high 节点值不在要求区间里面的时候直接return NULL。

不难写出如下代码：

一、初步构思错误代码

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr || root->val < low || root->val > high) return nullptr;
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

初步构思代码问题：

稍作分析就会发现，由于二叉搜索树的有序特性，当某个子树的根节点值小于区间下限时，其左子树一定小于区间下限，可以直接修剪掉，但是其右子树是有可能满足区间要求的不能直接修剪掉，而这个初步构思的代码错就错在如果遇到不满足区间要求的节点就直接return NULL 的话，会误把不应该删除的节点删除掉，造成修剪过度，返回错误结果！

而进一步用递归的思想思考一下，可以分成两种情况：

1. 如果root（当前遍历到的节点）的数值小于low的数值，那么应该递归其右子树，并返回右子树符合条件的头结点。
2. 同理，如果root（当前遍历到的节点）的数值大于high的数值，那么应该递归其左子树，并返回左子树符合条件的头结点。
3. 而当root（当前遍历到的节点）的数值符合要求区间时，那么就正常向下递归其左子树和右子树就可以了！

二、最终优化正确解法

C++代码

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root) return nullptr;
        if(root->val < low) return trimBST(root->right, low, high);
        if(root->val > high) return trimBST(root->left, low, high);
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

这样，这道题就解决了！

总结

这道修剪二叉搜索树其实并不难，但如果没做过插入和删除二叉搜索树节点的题直接上来看这个思路其实是比较绕的。所以强烈建议大家先做一下做一下Leetcode701.二叉搜索树中的插入操作和Leetcode450. 删除二叉搜索树中的节点两道题，也可以直接看一下我上一篇文章的讲解：一文搞懂怎么删除二叉搜索树和普通二叉树节点
这道题会理解得更加清晰透彻！

---

欢迎大家扫码关注本人公众号：编程复盘与思考随笔

(关注后可以免费获得本人在csdn发布的资源源码)

公众号主要记录编程和刷题时的总结复盘笔记和心得！并且分享读书、工作、生活中的一些思考感悟！