C++刷题周记(三)——DFS/BFS/拓扑排序

本周将进入图论的学习，在此之前，我们需要了解dfs/bfs这两种经典的遍历方法

目录

DFS深度优先遍历

N皇后问题

树与图的存储

树与图的遍历

BFS宽度优先遍历

拓扑排序

---

DFS深度优先遍历

可以用dfs深度优先遍历思想（即回溯法）解决的题目：

模板题：Acwing 842 排列数字

N皇后问题

经典应用N皇后问题：Acwing 843    lc 51. N 皇后

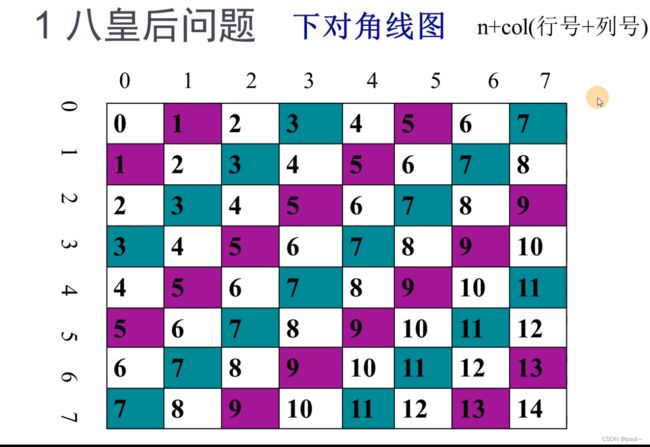
代码与题解如下，需要思考为什么此处需要手动模拟回溯过程，而树形结构不需要

// acwing 843
#include 
using namespace std;
const int N = 20;
int n;
// 存储棋盘
char g[N][N];
// col-列的状态
// dg-正对角线(右上-左下)  udg-反对角线(左上-右下)
bool col[N],dg[N],udg[N];

// 每一行必有一个皇后 对第u行进行深度遍历
void dfs(int u){
    // 如果已经遍历完所有行 即可输出结果
    if(u == n){
        for(int i = 0;i < n; i++){
            cout << g[i] << endl;
        }
        // 输出结果后return实现回溯
        cout << endl;return;
    }
    // 对于n皇后此类没有树形结构的问题
    // 需要手动模拟回溯过程 而树的遍历中隐含了回溯
    // 故不需要手动还原状态
    // 对第u行第i列进行逐列的遍历
    for(int i = 0; i < n; i++){
        // 对角线下标的对应方式参照题解中的图
        if(!col[i] && !dg[u + i] && !udg[u - i + n]){
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[u - i + n] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[u - i + n] = false;
            g[u][i] = '.';
        }
    }
}
int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin >> n;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < n; j++){
            g[i][j] = '.';
        }
    }
    dfs(0);
    return 0;
}

树与图的存储

需要注意的是，acwing中皆采用的是邻接表方式存储，使用数组来模拟链表，这样效率更高

做法与哈希表中拉链法的数组模拟是一致的

// 数组模拟链表  e[i] 节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 可以把idx理解为一个结点 e为其值 ne为后继指针
// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx,idx++;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);

而leetcode中的题都是使用的结构体来存储树与图，这样做起来是更好理解的，做题时根据具体情况区分辨析这两种方法

树与图的遍历

我们可以将树视为无向图，那么树与图的遍历皆可套用y总的模板，该模板比较适合在邻接表和传统型邻接矩阵下使用，在leetcode型邻接矩阵中使用不太方便

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

模板题：Acwing 846 树的重心

图的dfs遍历：lc 797. 所有可能的路径

该题的dfs与以上dfs模板属于两个流派，根本区别在于是否有需要手动添加终止条件

可以参照这篇：岛屿数量，说实话我还没有完全参透（之后顿悟了再填坑

树的dfs遍历：

二刷了些力扣题，对dfs中的回溯加深理解（lc中树的存储方式不同）：
lc 257. 二叉树的所有路径

需要思考C++函数什么时候应该传引用，什么时候应该直接传变量

此题的dfs函数参数中不带引用，不做地址拷贝，只做内容拷贝，以避免了每次手动回溯

(因为 -> 在string中需要pop两次，麻烦！)   但是牺牲了空间 需要谨慎

同时，对引用和指针进行了辨析 详情可参照这篇：C++ 引用详解(引用的特点，引用与指针的区别，引用的其他使用)_c++引用_Mi ronin的博客-CSDN博客

其他树的遍历的题：lc 112. 路径总和     lc 113. 路径总和 II

lc 104. 二叉树的最大深度   lc 111. 二叉树的最小深度

BFS宽度优先遍历

问题识别：边权为1 + 单源最短路问题  = BFS求解

模板伪代码如下，需要注意的是，state状态数组并不是必须的，可根据题意用其他条件表达相同效果。

void bfs(){
    queue q;
    st[1] = true; // 表示1号点已经被遍历过
    q.push(1);

    while (q.size())
    {
        int t = q.front();
        q.pop();
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (!s[j])
            {
                st[j] = true; // 表示点j已经被遍历过
                q.push(j);
            }
        }
    }
}

模板题：Acwing 847 （此题便通过距离数组d起到state状态数组的作用）

int h[N],e[N],ne[N],idx;// 邻接表存储
int d[N];// 保存1号点到各个点的距离
int bfs(){
    memset(d,-1,sizeof d);
    queue q;
    // 因为是从0开始遍历
    d[1] = 0;
    q.push(1);
    while(!q.empty()){
        int t = q.front();
        q.pop();
        for(int i = h[t]; i!=-1;i = ne[i]){
            int j = e[i];
            // 因为存在自环与重边 所以需要此判断
            // 距离d实际上起到了state的作用
            if(d[j] == -1){
                d[j] = d[t] + 1;
                q.push(j);
            }
        }
    }
    return d[n];
}

应用题：Acwing 844 走迷宫    参考资料：AcWing 844. 走迷宫：图解+代码注释 - AcWing

// 使用pair构建存储坐标的基本类型
typedef pair PII;
const int N = 110;
int n,m;
int g[N][N];// 存储迷宫地图
int d[N][N];// 存储每个点到起点的距离
int bfs(int a,int b){
    queue q;
    // 将起始点加入队列
    q.push({a,b});
    // 把没走过的点设置为 -1
    memset(d,-1,sizeof d);
    // 将起始点赋值为 0
    d[a][b] = 0;
    // 模拟四个潜在的移动方向
    int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};
    while(!q.empty()){
        PII start = q.front();
        q.pop();
        for(int i = 0; i < 4;i++){
            int x = start.first + dx[i];
            int y = start.second + dy[i];
            // 此限制条件就决定了bfs所得到的是最短路径
            if( x>=0&&x=0&&y

此题也是通过各种限制条件，让bfs不走回头路，以达到state数组的效果 

与本题情境相似的一道题：lc 200. 岛屿数量

拓扑排序

适用范围：有向无环图

算法思路：（本质上就是基于BFS的思想）

• 一个有向无环图，如果图中有入度为0的点，就把该点删掉，同时也删掉该点所连接的所有边

（翻译成程序语言：所有入度为0的点入队，从队列中出队一个点并放入top序列数组中，与该点相邻的所有点入度 -1 ）

• 循环以上 出队、加入序列数组、相邻点入度-1的操作，直至队列为空。此时若序列数组大小与原数组大小一致，代表可以进行拓扑排序，反之则不能。ps：拓扑序列是不一定唯一的

模板题：Acwing 848 有向图的拓扑序列          参考资料

vector top;// 存放拓扑序列
int d[N];// 记录节点的入度

void topsort(){
    queue q;
    int t;
    for(int i = 1;i <= n;i++){
        // 遍历全图，将入度为0的点入队
        if(d[i] == 0){
            q.push(i);
        }
    }
    // 对图中入度为0的点进行循环处理
    while(!q.empty()){
        t = q.front();
        q.pop();
        top.push_back(t);
        // 将 以入度为0点为起点的边 全部删去
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            d[j]--;// 即删除边所指向终点的入度
            if(d[j] == 0){
                q.push(j);
            }
        }
    }
    if(top.size() < n)   cout << "-1";
    else {
        for(int i = 0;i < n; ++i){
            cout << top[i] <<" ";
        }
    }
}

这个模板十分好用，可以ac这两道题 lc207. 课程表   lc210. 课程表 II

因为拓扑序列具有不唯一性，我们应如何判断是否有唯一的拓扑序呢？

其实很简单，在以上模板中，每一次while循环的最开始，对当前队列中的元素个数进行判断，如果队列元素个数大于1，即不存在唯一的拓扑序。若每一层while循环皆能保持队列元素个数为1，则存在唯一拓扑序。