leetcode第 69 场双周赛

第 69 场双周赛

题目

5960.将标题首字母大写

题目大意

给你一个字符串 title ，它由单个空格连接一个或多个单词组成，每个单词都只包含英文字母。请你按以下规则将每个单词的首字母 大写 ：

• 如果单词的长度为 1 或者 2 ，所有字母变成小写。
• 否则，将单词首字母大写，剩余字母变成小写。

请你返回 大写后 的 title 。

样例

数据规模

思路

比赛的时候使用的C++，所以分割字符串会比较麻烦，先将字符逐个加入到字符串s中，一旦检测到空格就中断，然后对字符串s长度进行判断，进行大小写的修改。（这样写的代码很麻烦）

代码

class Solution {
public:
    string capitalizeTitle(string title) {
        string s;
        string ans;
        for(int i=0;i<title.length();i++){
            if(title[i]!=' ')
                s+=title[i];
            else{
                if(s.length()<=2){
                    for(int j=0;j<s.length();j++){
                        if(s[j]>='A'&&s[j]<='Z')s[j]=s[j]-'A'+'a';
                    }
                    s+=' ';
                    ans+=s;
                }
                else{
                    if(s[0]>='a'&&s[0]<='z')s[0]=s[0]-'a'+'A';
                    for(int j=1;j<s.length();j++){
                        if(s[j]>='A'&&s[j]<='Z')s[j]=s[j]-'A'+'a';
                    }
                    s+=' ';
                    ans+=s;
                }
                s="";
            }
        }
        if(s.length()<=2){
                    for(int j=0;j<s.length();j++){
                        if(s[j]>='A'&&s[j]<='Z')s[j]=s[j]-'A'+'a';
                    }
                    s+=' ';
                    ans+=s;
                }
                else{
                    if(s[0]>='a'&&s[0]<='z')s[0]=s[0]-'a'+'A';
                    for(int j=1;j<s.length();j++){
                        if(s[j]>='A'&&s[j]<='Z')s[j]=s[j]-'A'+'a';
                    }
                    s+=' ';
                    ans+=s;
                }
        string s2;
        for(int i=0;i<ans.length()-1;i++)s2+=ans[i];
        return s2;
    }
};

思路2

整体思路不变，但改成使用python语言，C++麻烦主要麻烦在字符串分割。而python可以直接使用title.split(' ')就可以直接将字符串逐个分出来，然后查看长度并且使用upper和lower函数直接大小写修改。

代码2

class Solution:
    def capitalizeTitle(self, title: str) -> str:
        words=title.split(' ')
        ans=''
        for word in words:
            if len(word) in (1,2):
                ans+=word.lower()+' '
            else:
                ans+=word[0].upper()+word[1:].lower()+' '
        return ans[:-1]

题目

5961.链表最大孪生和

题目大意

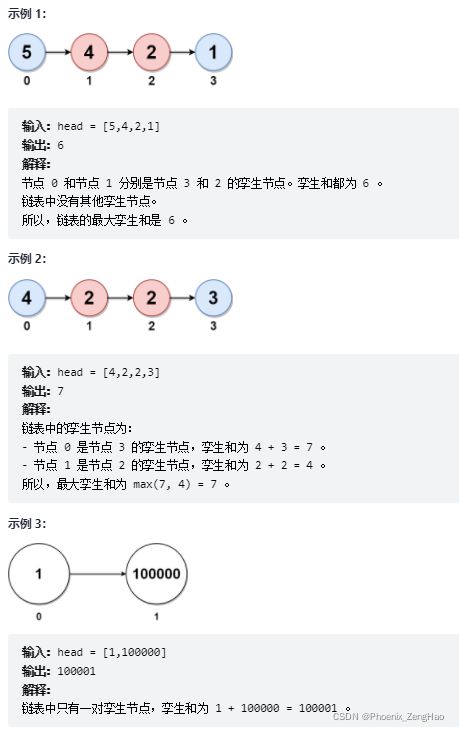
在一个大小为 n 且 n 为 偶数 的链表中，对于 0 <= i <= (n / 2) - 1 的 i ，第 i 个节点（下标从 0 开始）的孪生节点为第 (n-1-i) 个节点 。

• 比方说，n = 4 那么节点 0 是节点 3 的孪生节点，节点 1 是节点 2 的孪生节点。这是长度为 n = 4 的链表中所有的孪生节点。

孪生和 定义为一个节点和它孪生节点两者值之和。

给你一个长度为偶数的链表的头节点 head ，请你返回链表的 最大孪生和 。

样例

数据规模

思路

直接把链表中的所有数据存储到数组a中，而它们数量一定是偶数，所以可以左右数字两两相加，更新答案。

代码

class Solution {
public:
    int pairSum(ListNode* head) {
        vector<int>a;
        while(head!=nullptr){
            a.push_back(head->val);
            head=head->next;
        }
        int ans=0;
        for(int i=0;i<a.size()/2;i++){
            ans=max(ans,a[i]+a[a.size()-1-i]);
        }
        return ans;
    }
};

题目

5962.连接两字母单词得到的最长回文串

题目大意

给你一个字符串数组 words 。words 中每个元素都是一个包含 两个 小写英文字母的单词。

请你从 words 中选择一些元素并按 任意顺序 连接它们，并得到一个 尽可能长的回文串 。每个元素 至多 只能使用一次。

请你返回你能得到的最长回文串的 长度 。如果没办法得到任何一个回文串，请你返回 0 。

回文串 指的是从前往后和从后往前读一样的字符串。

样例

数据规模

思路

观察数据发现字符串一定长度等于2，那么一定是$XX$的形式（X指代字母），那么完全可以用一个整数来替代$XX$，比如$ab=1\ast 26+2,yz=25\ast 26+26$，这样就可以保证任意两个字符串可以实现从字符串到INT的映射。然后将每一种字符串的数量进行计数。如果字符串中两个字母不同，比如：ab这种字符串，它只能和ba进行组合分别放到左右两端，那么数量贡献=$(min(tot[i\ast 26+j],tot[j\ast 26+i]))，$对于长度贡献需要*4（因为数量是配对的数量，字符串数量是其两倍，长度是字符串数量的两倍）。如果字符串中两个字母相同，比如：aa这种字符串，它可以和别的aa进行组合，也可以将它放在中间位置，和和别的aa进行组合方式和刚才的情况类似。期间需要将配对过的类型数量减掉，最后看是否存在aa这种字符串，直接对长度答案贡献+2（只能贡献一次）。

代码

class Solution
{
public:
int vis[100000+50],tot[100000+50];
    int longestPalindrome(vector<string> &words)
    {
        int n = words.size();
        int ans=0;
        for (int i = 0; i < n; i++)
        {
            string s = words[i];
            tot[(s[0]-'a'+1)*26+(s[1]-'a'+1)]++;
        }
        for(int i=1;i<=26;i++){
            for(int j=i;j<=26;j++){
                if(i==j){
                    ans=ans+4*(min(tot[i*26+j],tot[j*26+i])/2);
                    tot[i*26+j]-=min(tot[i*26+j],tot[j*26+i])/2*2;
                }
                else{
                    ans=ans+4*(min(tot[i*26+j],tot[j*26+i]));
                    tot[i*26+j]-=min(tot[i*26+j],tot[j*26+i]);
                    tot[j*26+i]-=min(tot[i*26+j],tot[j*26+i]);
                }
                
            }
        }
        for(int i=1;i<=26;i++){
            if(tot[i*26+i]>=1){
                ans+=2;
                break;
            }
        }
        return ans;
    }
};

题目

5931.用邮票贴满网格图

题目大意

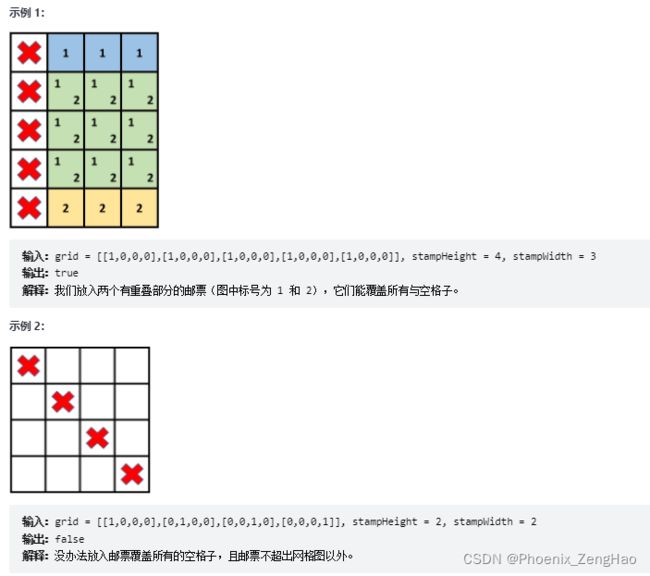
给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

• 覆盖所有 空 格子。
• 不覆盖任何 被占据 的格子。
• 我们可以放入任意数目的邮票。
• 邮票可以相互有 重叠 部分。
• 邮票不允许 旋转 。
• 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

样例

数据规模

思路

此题需要使用二维前缀和。二位前缀和类似于一维前缀和（就是题目1中的前缀累加和），二维前缀和就是一个矩阵的总和，比如：$sum[x1][y1]$就是左上角小矩阵的总和。如果要计算矩阵（x1,y1,x2,y2）的总和，就相当于$sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1+1]$

先考虑此题需要的二维前缀和：$sum[i][j]$表示矩阵(1,1,i,j)之前多少个未被占据的格子。（我将数据从0开始改为了从1开始）

对于这个题来讲对于每一个未被占据的格子（不是未被邮票粘贴的格子），判断它是否可以作为左上角进行邮票粘贴，那么如果粘贴了邮票，它的右下角就是(i+stampHeight-1,j+stampWidth-1)，左上角就是(i,j)，要保证它中间不存在被占据的格子，那么矩阵直接的未被占据的格子数量=$stampHeight\ast stampWidth$，说明此时点(i,j)可以作为左上角进行邮票粘贴。

此时又需要维护一个二维前缀和：$q[i][j]$表示点(i,j)有几个邮票覆盖着。

一旦有一个邮票可以进行粘贴，那么就要维护$q[i][j]$，即对于邮票的左上角$q[i][j]++,q[ix+1][iy+1]++,q[i][iy+1]--,q[ix+1][j]--$，这其实就相当于上述计算矩阵（x1,y1,x2,y2）的总和的逆过程，我当前$q[i][j]$本身是空的，现在对于一个矩阵的所有点进行的+1操作，那么就可以对左上角+1，但是为了避免矩阵外的点进行+1操作，就需要在右上角和左下角-1操作进行抵消，但是两次-1操作会导致右下角多-1，所以需要+1进行抵消（简单的容斥原理，可以画矩阵图理解）。最后将$q[i][j]$进行前缀和叠加，看是否存在未被占据的点没有邮票覆盖，如果存在就false，否则就是true。

代码

class Solution {
public:

    bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
        int n=grid.size(),m=grid[0].size();
        vector<vector<int>>a(n+5,vector<int>(m+5));
        vector<vector<int>>sum(n+5,vector<int>(m+5));
        vector<vector<int>>q(n+5,vector<int>(m+5));
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i+1][j+1]=1-grid[i][j];
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]; 
                // cout<
            }
            // cout<
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                int ix=i+stampHeight-1,iy=j+stampWidth-1;
                if(ix>n||iy>m||a[i][j]==0)continue;
                // cout<
                if(sum[ix][iy]-sum[i-1][iy]-sum[ix][j-1]+sum[i-1][j-1]==stampHeight*stampWidth){
                    // cout<
                    q[i][j]++;
                    q[i][iy+1]--;
                    q[ix+1][j]--;
                    q[ix+1][iy+1]++;
                }
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                q[i][j]+=q[i-1][j]+q[i][j-1]-q[i-1][j-1]; 
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(a[i][j]==0)continue;
                if(q[i][j]==0)return 0;
            }
            cout<<endl;
        }
        return 1;
    }
};