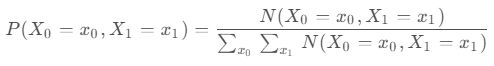【数据处理】Python:实现求联合分布的函数 | 求边缘分布函数 | 概率论 | Joint distribution | Marginal distribution
![]() 猛戳订阅! 《一起玩蛇》
猛戳订阅! 《一起玩蛇》
写在前面:本章我们将通过 Python 手动实现联合分布函数和边缘分布函数,部署的测试代码放到文后了,运行所需环境 python version >= 3.6,numpy >= 1.15,nltk >= 3.4,tqdm >= 4.24.0,scikit-learn >= 0.22。
0x00 实现求联合分布的函数(Joint distribution)
请完成下面的代码,计算联合分布函数 (Joint distribution),使用的两个随机变量如下:
- 为 test 中 word0 的出现次数。
- 为 test 中 word1 的出现次数。
求出上述 的联合分布函数,实现 joint_distribution_of_word_counts 函数。
提示:联合分布函数 (Joint distribution) 公式如下:
joint_distribution_of_word_counts 是用来计算提供的 test 中的两个 word 的函数。
输入 texts 和第一个单词 word0,第二个单词 word1 构成 ,要求返回 Pjoint:
def joint_distribution_of_word_counts(texts, word0, word1):
"""
Parameters:
texts (list of lists) - a list of texts; each text is a list of words
word0 (str) - the first word to count
word1 (str) - the second word to count
Output:
Pjoint (numpy array) - Pjoint[m,n] = P(X0=m,X1=n), where
X0 is the number of times that word0 occurs in a given text,
X1 is the number of times that word1 occurs in the same text.
"""
# TODO
return PJoint输出结果演示:
Problem1. Joint distribution
[[0.964 0.024 0.002 0. 0.002]
[0.006 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0.002 0. 0. 0. 0. ]]参考代码:joint_distribution_of_word_counts 的实现
from collections import Counter
def joint_distribution_of_word_counts(texts, word0, word1):
# 统计 word0 和 word1 在每个文本中的出现次数
word0_counts = [Counter(text)[word0] for text in texts]
word1_counts = [Counter(text)[word1] for text in texts]
# 获取 X0 和 X1 的最大计数
max_x0 = max(word0_counts)
max_x1 = max(word1_counts)
# 初始化联合分布矩阵
Pjoint = np.zeros((max_x0 + 1, max_x1 + 1))
# 填充联合分布矩阵
for x0, x1 in zip(word0_counts, word1_counts):
Pjoint[x0, x1] += 1
# 归一化以获得概率
Pjoint /= Pjoint.sum()
return Pjoint0x01 实现求边缘分布的函数(Marginal distribution)
实现求边缘分布 (Marginal distrubution) 的函数 marginal_distribution_of_word_counts。
使用 "问题1" 中求出 Pjoint 求边缘分布,函数形参为 Pjoint 和 index,其中:
- index 指的是在联合分布中保留哪个随机变量,而对另一个进行边缘化。
- 边缘分布是从联合分布中消除某些变量以获取其他变量的分布。
使用 Pjoint 中给出的 index 计算其边缘分布,并将结果储存到 Pmarginal 变量中并予以返回。
提示:边缘分布 (Marginal distrubution) 的公式如下:
def marginal_distribution_of_word_counts(Pjoint, index):
"""
Parameters:
Pjoint (numpy array) - Pjoint[m,n] = P(X0=m,X1=n), where
X0 is the number of times that word0 occurs in a given text,
X1 is the number of times that word1 occurs in the same text.
index (0 or 1) - which variable to retain (marginalize the other)
Output:
Pmarginal (numpy array) - Pmarginal[x] = P(X=x), where
if index==0, then X is X0
if index==1, then X is X1
"""
raise RuntimeError("You need to write this part!")
return Pmarginal
输出结果演示:
Problem2. Marginal distrubution:
P0: [0.992 0.006 0. 0. 0.002]
P1: [0.972 0.024 0.002 0. 0.002]参考代码:joint_distribution_of_word_counts 的实现
def marginal_distribution_of_word_counts(Pjoint, index):
Pmarginal = np.sum(Pjoint, axis = 1 - index) # 沿指定轴 index 求和
return Pmarginal根据公式,我们可以使用 使用 np.sum 函数来计算边缘分布:
通过 np.sum(Pjoint, axis = 1 - index) 在 Pjoint 数组中 对非 index 的轴进行求和。
就可以得到边缘分布,axis 表示沿着哪个轴进行操作,这里我们设置为 1 - index 是因为:
- 如果
index=0,我们想要保留 ,那么我们需要对 进行边缘化,即沿着轴 1 进行求和。因此,axis = 1 - 0 = 1。 - 如果
index=1,我们想要保留 ,那么我们需要对 进行边缘化,即沿着轴 0 进行求和。因此,axis = 1 - 1 = 0。
0x03 提供测试用例
这是一个处理文本数据的项目,测试用例为 500 封电子邮件的数据(txt 的格式文件):
![]()
所需环境:
- python version >= 3.6
- numpy >= 1.15
- nltk >= 3.4
- tqdm >= 4.24.0
- scikit-learn >= 0.22nltk 是 Natural Language Toolkit 的缩写,是一个用于处理人类语言数据(文本)的 Python 库。nltk 提供了许多工具和资源,用于文本处理和 NLP,PorterStemmer 用来提取词干,用于将单词转换为它们的基本形式,通常是去除单词的词缀。 RegexpTokenizer 是基于正则表达式的分词器,用于将文本分割成单词。
data_load.py:用于加载文本数据
import os
import numpy as np
from nltk.stem.porter import PorterStemmer
from nltk.tokenize import RegexpTokenizer
from tqdm import tqdm
porter_stemmer = PorterStemmer()
tokenizer = RegexpTokenizer(r"\w+")
bad_words = {"aed", "oed", "eed"} # these words fail in nltk stemmer algorithm
def loadFile(filename, stemming, lower_case):
"""
Load a file, and returns a list of words.
Parameters:
filename (str): the directory containing the data
stemming (bool): if True, use NLTK's stemmer to remove suffixes
lower_case (bool): if True, convert letters to lowercase
Output:
x (list): x[n] is the n'th word in the file
"""
text = []
with open(filename, "rb") as f:
for line in f:
if lower_case:
line = line.decode(errors="ignore").lower()
text += tokenizer.tokenize(line)
else:
text += tokenizer.tokenize(line.decode(errors="ignore"))
if stemming:
for i in range(len(text)):
if text[i] in bad_words:
continue
text[i] = porter_stemmer.stem(text[i])
return text
def loadDir(dirname, stemming, lower_case, use_tqdm=True):
"""
Loads the files in the folder and returns a
list of lists of words from the text in each file.
Parameters:
name (str): the directory containing the data
stemming (bool): if True, use NLTK's stemmer to remove suffixes
lower_case (bool): if True, convert letters to lowercase
use_tqdm (bool, default:True): if True, use tqdm to show status bar
Output:
texts (list of lists): texts[m][n] is the n'th word in the m'th email
count (int): number of files loaded
"""
texts = []
count = 0
if use_tqdm:
for f in tqdm(sorted(os.listdir(dirname))):
texts.append(loadFile(os.path.join(dirname, f), stemming, lower_case))
count = count + 1
else:
for f in sorted(os.listdir(dirname)):
texts.append(loadFile(os.path.join(dirname, f), stemming, lower_case))
count = count + 1
return texts, count
reader.py:将读取数据并打印
import data_load, hw4, importlib
import numpy as np
if __name__ == "__main__":
texts, count = data_load.loadDir("data", False, False)
importlib.reload(hw4)
Pjoint = hw4.joint_distribution_of_word_counts(texts, "mr", "company")
print("Problem1. Joint distribution:")
print(Pjoint)
print("---------------------------------------------")
P0 = hw4.marginal_distribution_of_word_counts(Pjoint, 0)
P1 = hw4.marginal_distribution_of_word_counts(Pjoint, 1)
print("Problem2. Marginal distribution:")
print("P0:", P0)
print("P1:", P1)
print("---------------------------------------------")
Pcond = hw4.conditional_distribution_of_word_counts(Pjoint, P0)
print("Problem3. Conditional distribution:")
print(Pcond)
print("---------------------------------------------")
Pathe = hw4.joint_distribution_of_word_counts(texts, "a", "the")
Pthe = hw4.marginal_distribution_of_word_counts(Pathe, 1)
mu_the = hw4.mean_from_distribution(Pthe)
print("Problem4-1. Mean from distribution:")
print(mu_the)
var_the = hw4.variance_from_distribution(Pthe)
print("Problem4-2. Variance from distribution:")
print(var_the)
covar_a_the = hw4.covariance_from_distribution(Pathe)
print("Problem4-3. Covariance from distribution:")
print(covar_a_the)
print("---------------------------------------------")
def f(x0, x1):
return np.log(x0 + 1) + np.log(x1 + 1)
expected = hw4.expectation_of_a_function(Pathe, f)
print("Problem5. Expectation of a function:")
print(expected)
![]()
[ 笔者 ] foxny
[ 更新 ] 2023.11.14
❌ [ 勘误 ] /* 暂无 */
[ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
本人也很想知道这些错误,恳望读者批评指正!| 参考资料 C++reference[EB/OL]. []. http://www.cplusplus.com/reference/. Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/. |