算法设计与分析复习--递归与分治(二)
文章目录
- 上一篇
- 归并排序
- 统计逆序对
- 快速排序
- 线性时间选择
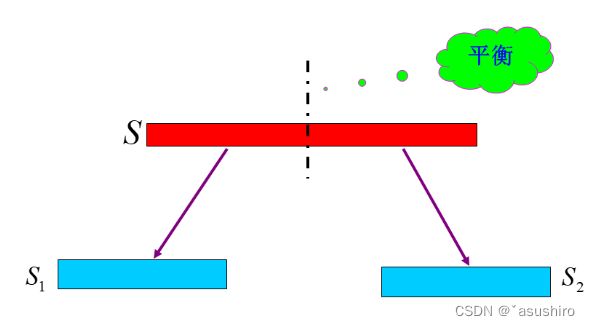
- 最接近点对问题
-
- 一维
- 二维
- 循环赛日程表
- 下一篇
上一篇
算法设计与分析复习–递归与分治(一)
归并排序
问题特点:局部有序到整体有序
AcWing787.归并排序
#include
#include
#include
using namespace std;
const int N = 100010;
int a[N];
int n;
void merge_sort(int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(l, mid); merge_sort(mid + 1, r);
int i = l, j = mid + 1;
int temp[N], k = 0;
while (i <= mid && j <= r)
{
if (a[i] <= a[j]) temp[k ++] = a[i ++];
else temp[k ++] = a[j ++];
}
while (i <= mid) temp[k ++] = a[i ++];
while (j <= r) temp[k ++] = a[j ++];
for (int i = l, j = 0; i <= r; i ++, j ++)
{
a[i] = temp[j];
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++) scanf("%d", &a[i]);
merge_sort(0, n - 1);
for (int i = 0; i < n; i ++)
printf("%d ", a[i]);
return 0;
}
详解
统计逆序对
AcWing788.逆序对的数量
#include
#include
#include
#define int long long
using namespace std;
const int N = 100010;
int a[N], n;
int merge_sort(int l, int r)
{
if (l >= r) return 0;
int mid = l + r >> 1;
int res = merge_sort(l, mid) + merge_sort(mid + 1, r);
int i = l, j = mid + 1, tmp[N], k = 0;
while (i <= mid && j <= r)
{
if (a[i] <= a[j]) tmp[k ++] = a[i ++];
else{
tmp[k ++] = a[j ++];
res += mid - i + 1;// 左边的a[i]大时,左边后面的数也都大于因此加在一起,因为是左边一堆对上右边一个,所以不存在重复
}
}
while (i <= mid) tmp[k ++] = a[i ++];
while (j <= r) tmp[k ++] = a[j ++];
for (int i = l, j = 0; i <= r; i ++, j ++)
a[i] = tmp[j];
return res;
}
signed main()
{
scanf("%lld", &n);
for (int i = 0; i < n; i ++) scanf("%d", &a[i]);
printf("%lld", merge_sort(0, n - 1));
return 0;
}
快速排序
up讲解
AcWing785.快速排序
#include
#include
#include
using namespace std;
const int N = 100010;
int a[N], n;
void quick_sort(int l, int r)
{
if (l >= r) return;
int x = a[l + rand() % (r - l + 1)];
int i = l - 1, j = r + 1;
while (i < j)
{
while (a[++ i] < x);
while (a[-- j] > x);
if (i < j) swap(a[i], a[j]);
}
quick_sort(l, j); quick_sort(j + 1, r);
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++) scanf("%d", &a[i]);
quick_sort(0, n - 1);
for (int i = 0; i < n; i ++)
printf("%d ", a[i]);
return 0;
}
详解
线性时间选择
求一个有序序列的中位数
方法:利用topk问题及中位数的性质进行求解
AcWing786.第k个数
中位数:
#include
#include
#include
using namespace std;
const int N = 100010;
int a[N], n, k;
int quick_sort(int l, int r, int k)
{
if (l >= r) return a[l];
int x = a[l + rand() % (r - l + 1)];
int i = l - 1, j = r + 1;
while (i < j)
{
while (a[++ i] < x);
while (a[-- j] > x);
if (i < j) swap(a[i], a[j]);
}
int left = j - l + 1;
if (k <= left) return quick_sort(l, j, k);
else return quick_sort(j + 1, r, k - left);
}
int main()
{
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
// printf("%d", quick_sort(1, n, k));
if (n % 2) printf("%d\n", quick_sort(1, n, n / 2));
else printf("%d\n", quick_sort(1, n, n / 2) + quick_sort(1, n, n / 2 + 1) >> 1);
return 0;
}
最接近点对问题
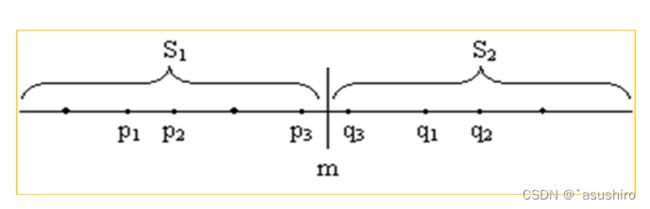
一维
#include
#include
using namespace std;
const int N = 100010;
int a[N], n;
int Cpair1(int l, int r) {
int num = r - l + 1;
if(num < 2) return a[l];
int m = (l + r) >> 1; // 中位数索引
int dl = Cpair1(l, m);
int dr = Cpair1(m + 1, r);
int dm = a[m + 1] - a[m]; // 计算中间两个数的差值
return min({dl, dr, dm});
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
sort(a, a + n); // 先对数组进行排序
int result = Cpair1(0, n - 1);
printf("%d\n", result);
return 0;
}
自己敲的,没有答案,有误请提出,谢谢
二维
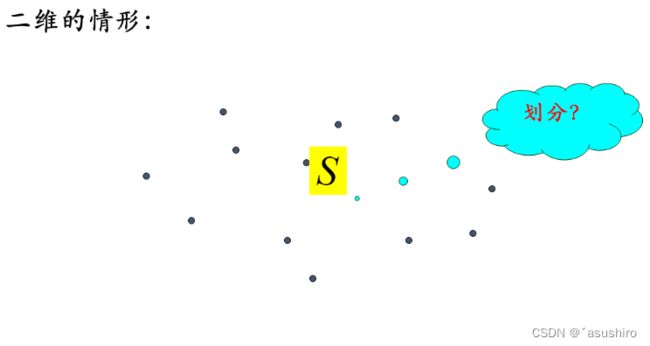


和一维相似,三个部分的最小值
但是二维为了缩减计算量,要先算出d的值,进而减少要计算点的个数

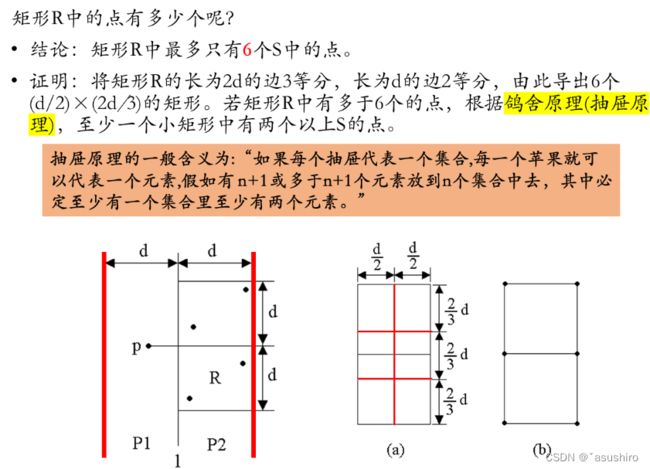
R这个矩形中由于已经有了两边的最小距离为d的这样的一个条件了所以,对R进行划分,在这样的条件下,每个小格子中最多有一个点,当有两个点时就与最小距离为d这个条件矛盾了


循环赛日程表
#include
#include
#include
using namespace std;
const int N = 100;
int a[N][N];
void copy(int x1, int y1, int x2, int y2, int n)
{
for (int i = 0; i < n; i ++)
for (int j = 0; j < n; j ++)
a[x2 + i][y2 + j] = a[x1 + i][y1 + j];
}
void table(int i, int j, int n)
{
if (n == 1) return;
if (n > 1)
{
//求左上角的表
table(i, j, n / 2);
//求有上角的表
table(i, j + n / 2, n / 2);
//将左上角复制到右下角
copy(i, j, i + n / 2, j + n / 2, n / 2);
//将右上角复制到左下角
copy(i, j + n / 2, i + n / 2, j, n / 2);
}
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i ++) a[1][i] = i;//必须要初始化
table(1, 1, n);//起始坐标为(1, 1)
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= n; j ++)
{
printf("%d ", a[i][j]);
}
puts("");
}
return 0;
}
下一篇
算法设计与分析复习–动态规划(一)