C语言第入门——第十六课

目录

一、分治策略与递归

二、递归

1.求解n的阶乘

2.输入整数、倒序输出

3.输入整数、正序输出 

4.计算第n位Fibonacci数列

​编辑5.无序整数数组打印

6.找到对应数组下标 

---

一、分治策略与递归

在我们遇到大问题的时候，我们的正确做法是将它分解成小问题，然后一个小问题一个小问题解决，这样的策略就是分治策略。

递归是分治策略的一种方式，可以不断地通过自己调用自己来将问题规模逐渐缩小，从而解决问题。

分治策略的特征：

①大规模问题化成小规模问题容易被解决掉

②大规模问题能够被划分为多个相同的小规模问题

③这些小规模问题的解组合起来是大问题的解

④小规模问题是相互独立的

举个例子：

皇帝让你数10个谷仓的米粒，问题规模太大，你可以找100个工人，每人分上相同重量的米进行数，每个人的数量相加就是最终米粒的数量。

这就是一个典型的分治策略问题，将大规模转化为小规模问题，而且是满足上面分治策略的四条特征的。

分治策略不光在我们算法中需要使用，我希望转化成我们的思维模式，帮助我们更好的解决生活中的问题。

二、递归

递归包含两个过程：递推和回归，递推逐层调用，直到递推终止条件满足，再逐层回归。

递归和普通函数调用类似，需要开辟栈帧空间，它只有满足中止条件逐层回归的时候，上一层的函数的栈帧空间才会被释放。注意，不存在无限递归的函数，因为栈帧空间是有限的，所以不能无限调用函数，开辟空间。

递归分为直接递归和间接递归。

直接递归：在函数执行的时候调用函数自身。

间接递归：在函数执行过程中调用其他函数，再调用函数自身。

一般不推荐使用间接递归，因为很容易递推错误。

1.求解n的阶乘

代码如下：

int fabi(int n)
{
	if (n == 1) return 1;
	int sum = fabi(n-1)*n;
	return sum;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int sum =fabi(n);
	printf("%d", sum);
}

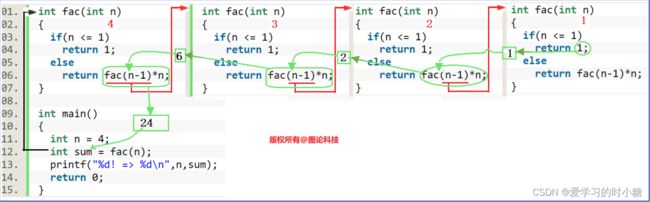
分析：我们将代码复制多份便于观看，但其实只有一个代码哦。

我们这里取n=4，第一次进入到fabi()函数中，n!=1，执行下一条语句fabi(n-1)*n，也就是fabi(3)*4。

然后我们再次调用函数fabi(),此时n=3,我们进入到函数体中n!=1，执行下一条语句fabi(2)*3。

此时我们再次调用fabi()函数，此时n=2，n!=1，执行fabi(1)*2。

这里再次调用fabi()函数，此时n==1，所以我们return 1。

返回到上一层，我们继续执行，此时这条语句为sum = 1*2,我们返回1*2,然后我们继续回归上一层函数，sum = 3*2*1，然后我们再回归，最后得到sum =4*3*2*1，回归结束。

下面第一张是我画的示意图，如果看不清楚再看下面第二张老师画的图，老师画的比较清晰。

红色的线代表递推过程，绿色的线代表回归过程。

 下面解释一下栈帧的动态变化情况。

在每次递推调用函数的时候，程序开辟栈帧空间，在回归的时候再一层层释放掉。

2.输入整数、倒序输出

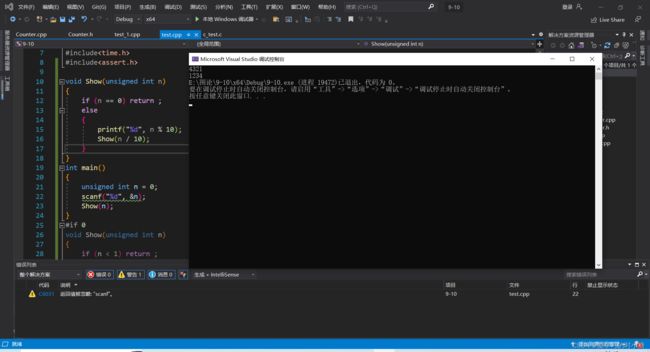
输入一个整数（无符号整型），使用递归算法将整数倒序输出。

void Show(unsigned int n)
{
	if (n == 0) return ;
	else
	{
		printf("%d", n % 10);
		Show(n / 10);
	}
}
int main()
{
	unsigned int n = 0;
	scanf("%d", &n);
	Show(n);
}

逻辑图如下，变量和函数定义不太一样，但是逻辑一致。

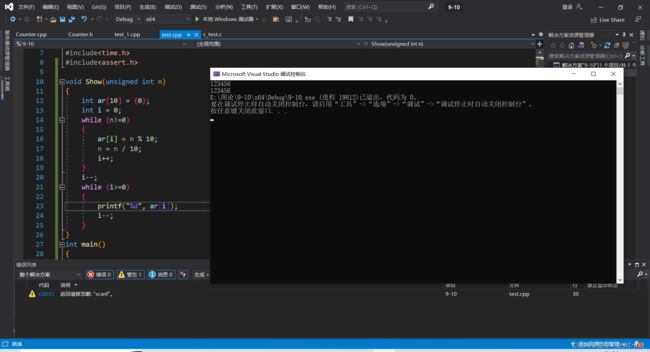
3.输入整数、正序输出 

法一：数组法

void Show(unsigned int n)
{	
	int ar[10] = {0};
	int i = 0;
	while (n!=0)
	{
		ar[i] = n % 10;
		n = n / 10;
		i++;
	}
	i--;
	while (i>=0)
	{
		printf("%d ", ar[i]);
		i--;
	}
}
int main()
{
	unsigned int n = 0;
	scanf("%d", &n);
	Show(n);
}

法二：递归法

void Show(unsigned int n)
{
	if (n == 0) return;
	else
	{
		Show(n / 10);
		printf("%d", n % 10);

	}
}
int main()
{
	unsigned int n = 0;
	scanf("%d", &n);
	Show(n);
}

4.计算第n位Fibonacci数列

法一：循环输出

int Fibonna(int n)
{
	int a = 1;
	int b = 1;
    if (n==0) return 0;
	if (n == 1 || n == 2)
	{
		return 1;
	}
	else
	{
		int i = 0;
		int temp = 0;
		int result = 0;
		while (i

法二：递归输出

int Fibonna(int n)
{
    if (n == 0) return 0;
	if (n == 1|| n == 2)
	{
		return 1;
	}
	else
	{
		return (Fibonna(n - 1) + Fibonna(n - 2));
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int result =Fibonna(n);
	printf("%d",result);
}

Q: 使用递归进行输出的时候空间复杂度是2^n，很大，怎么样降低时间复杂度？

A: 想要降低复杂度，主要就是要减少一个递归函数，将递归过程中的值存储下来就能减少相应的复杂程度。

写法一：一定要注意a,b,temp不能每次被调用的时候都初始化，要不然输出的值不正确。

int fac(int n)
{
	static int a = 1;
	static int b = 1;
	static int temp = 1;
	if (n <= 2) return temp;
	temp = a + b;
	b = a;
	a = temp;
	fac(n - 1);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int result = fac(n);
	printf("%d", result);
}

写法二：思路一致，只不过老师写的更清楚明了。

int fanc(int n, int a, int b)
{
	if (n <= 2) return a;
	else return fanc(n - 1, a + b, a);
}
int fac(int n)
{
	int a = 1;
	int b = 1;
	return fanc(n, a, b);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int result = fac(n);
	printf("%d", result);
}

5.无序整数数组打印

有一个整型数组，数值无序，使用循环和递归打印和查询。

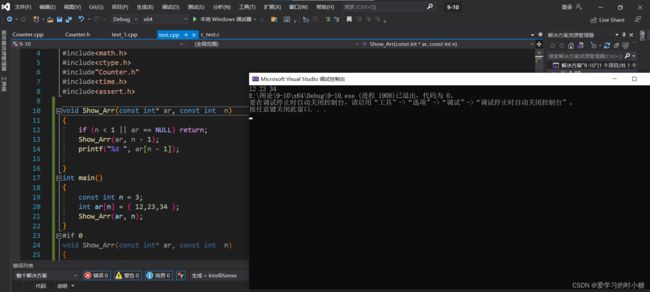
法一：循环打印

void Show_Arr(const int* ar, const int  n)
{
	if (n < 1 || ar == NULL) return;
	for (int i = 0; i < n; i++)
	{
		printf("%d ", ar[i]);
	}
}
int main()
{
	const int n = 3;
	int ar[n] = { 12,23,34 };
	Show_Arr(ar,n);
}

法二：使用递归打印数组

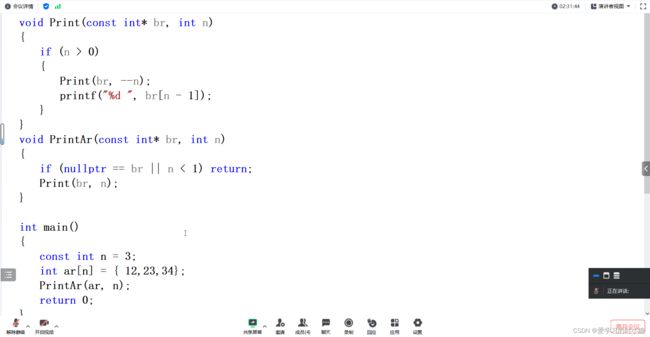
void Show_Arr(const int* ar, const int  n)
{
	if (n < 1 || ar == NULL) return;
	Show_Arr(ar, n - 1);
	printf("%d ", ar[n - 1]);

}
int main()
{
	const int n = 3;
	int ar[n] = { 12,23,34 };
	Show_Arr(ar, n);
}

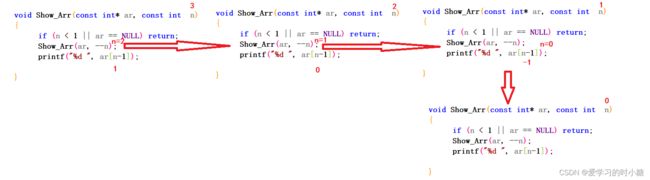
Q:上述递归代码我可可以将n-1修改成n--吗？请详细说明。

A:不可以修改，后置--是先取值后--，在下面示例中，n=3，n>0,调用函数，调用的新的函数还是n=3的函数，进入到一个循环，直到栈帧空间被填满。

Q:上述递归代码我可可以将n-1修改成--n吗？请详细说明。

A:也不可以修改，前置--是先--再取值，的确可以满足递归调用的逻辑，但是当他进行回归的时候会n的值被更改了，输出的是更改后的n-1，造成数据溢出问题。

6.找到对应数组下标 

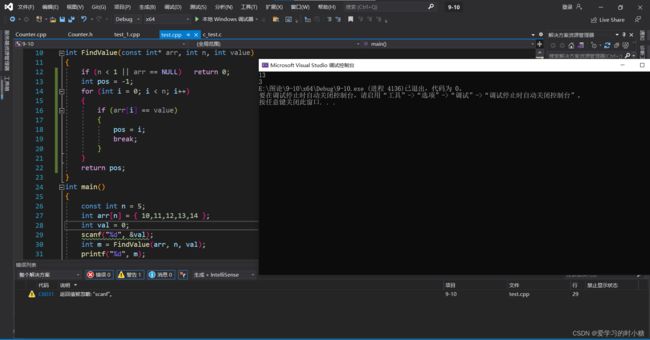
法一：循环找数组下标

int FindValue(const int* arr, int n, int value)
{
	if (n < 1 || arr == NULL)	return 0;
	int pos = -1;
	for (int i = 0; i < n; i++)
	{
		if (arr[i] == value)
		{
			pos = i;
			break;
		}
	}
	return pos;
}
int main()
{
	const int n = 5;
	int arr[n] = { 10,11,12,13,14 };
	int val = 0;
	scanf("%d", &val);
	int m = FindValue(arr, n, val);
	printf("%d", m);
}

法二：递归找数组下标

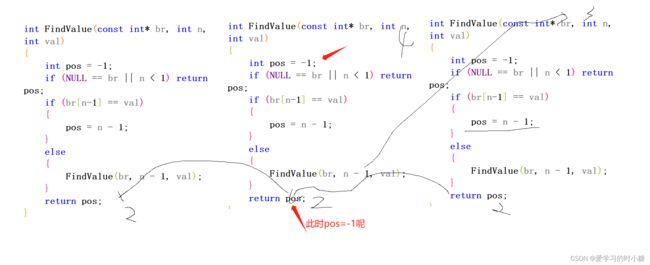
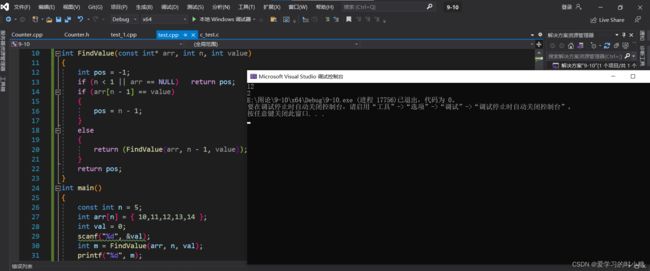
这面这个代码输出的数组下标有问题，一直是-1

int FindValue(const int* br, int n, int val)
{
	int pos = -1;
	if (NULL == br || n < 1) return pos;
	if (br[n-1] == val)
	{
		pos = n - 1;
	}
	else
	{
		FindValue(br, n - 1, val);
	}
	return pos;
}
int main()
{
	const int n = 5;
	int arr[n] = { 10,11,12,13,14 };
	int val = 0;
	scanf("%d", &val);
	int m=FindValue(arr,n,val);
	printf("%d", m);
}

正确代码 

int FindValue(const int* br, int n, int val)
{
	int pos = -1;
	if (NULL == br || n < 1) return pos;
	if (br[n-1] == val)
	{
		pos = n - 1;
	}
	else
	{
		pos =FindValue(br, n - 1, val);
	}
	return pos;
}
int main()
{
	const int n = 5;
	int arr[n] = { 10,11,12,13,14 };
	int val = 0;
	scanf("%d", &val);
	int m=FindValue(arr,n,val);
	printf("%d", m);
}