5.3 matlab数据插值（线性插值、最近点插值、埃尔米特插值、三次样条插值）
①数据插值可以根据有限个点的取值状况，合理估算出附近其他点的取值，从而节约大量的实验和测试资源，节省大量的人力、物力和财力。
②数据插值能够根据已知数据推算未知数据，这使得人们解决问题的能力得到了拓展和延伸。
1、引例-零件加工问题
例1、在飞机制造中，机翼的加工是一项关键技术。由于机翼尺寸很大，通常在图纸中只能标出一些关键点的数据。下表给出了某型飞机机翼的下缘轮廓线数据，求x每改变0.1时y的值。
它前段采样点稀疏，后段采样点密集，说明这段曲线前面可能比较规律、平滑，后段比较复杂
x = [0 3 5 7 9 11 12 13 14 15];
y = [0 1.2 1.7 2 2.1 2 1.8 1.2 1 1.6];
plot(x,y) %为插值前的曲线
hold on;
x1 = 0:0.1:15; %x每改变0.1要插一个值
y1 = interp1(x,y,x1,'spline'); %插值函数interp1:计算出这些插值点在y方向上的值存入y1中,y1很长
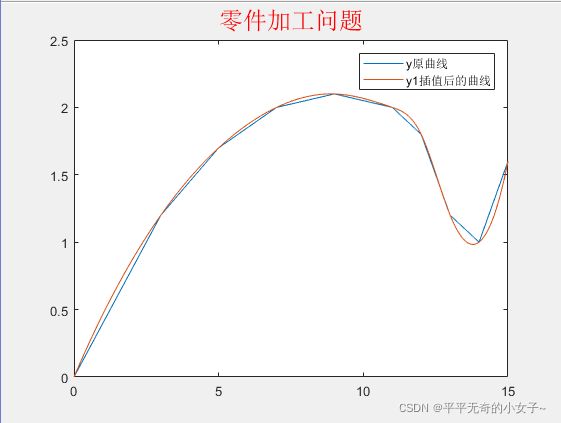
plot(x1,y1) %完成插值后的曲线，曲线变得光滑很多
legend('y原曲线','y1插值后的曲线')
title('零件加工问题','color','r','fontsize',18)
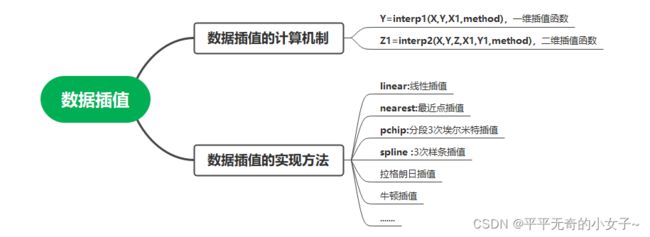
2、数据插值的计算机制
从数学上来说，数据插值是一种函数逼近的方法。
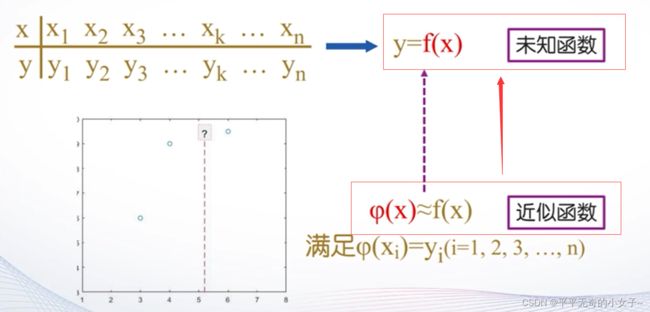（1）interp1( ):一维插值函数。调用格式:
Y=interp1(X,Y,X1,method)
根据X、Y的值,计算函数在×1处的值。其中，X、Y是两个等长的已知向量,分别表示采样点和采样值。X是一个向量或标量,表示要插值的点。
3、数据插值的实现方法
（1）一维插值method用于指定插值方法，常用的取值有以下四种:
①linear:线性插值，默认方法。
将与插值点靠近的两个数据点用直线连接，然后在直线上选取对应插值点的数据。
②nearest:最近点插值。
选择最近样本点的值作为插值数据。如果是中间点，则取后一个数据点的值。
③pchip:分段3次埃尔米特插值。
采用分段三次多项式，除满足插值条件，还需满足在若干节点处相邻段插值函数的一阶导数相等，使得曲线光滑的同时，还具有保形性。
④ spline :3次样条插值。
每个分段内构造一个三次多项式，使其插值函数除满足插值条件外，还要求在各节点处具有连续的一阶和二阶导数。（进—步提高了曲线的光滑性）
例2：以例1为例，进行四种数据插值的实现
x = [0 3 5 7 9 11 12 13 14 15];
y = [0 1.2 1.7 2 2.1 2 1.8 1.2 1 1.6];
x1 = 0:0.1:15; %x每改变0.1要插一个值
% plot(x,y)
% hold on
subplot(2,2,1)
y1 = interp1(x,y,x1,'linear'); %插值函数interp1:计算出这些插值点在y方向上的值存入y1中,y1很长
plot(x,y,x1,y1) %完成插值后的曲线
xlabel('interp1(x,y,x1,''linear'')','color','b')
legend('y','y1','location','northwest')
title('method = ''linear''','color','r','fontsize',14)
subplot(2,2,2)
y1 = interp1(x,y,x1,'nearest'); %插值函数interp1:计算出这些插值点在y方向上的值存入y1中,y1很长
plot(x,y,x1,y1) %完成插值后的曲线
xlabel('interp1(x,y,x1,''nearest'')','color','b')
legend('y','y1','location','northwest')
title('method = ''nearest''','color','r','fontsize',14)
subplot(2,2,3)
y1 = interp1(x,y,x1,'pchip'); %插值函数interp1:计算出这些插值点在y方向上的值存入y1中,y1很长
plot(x,y,x1,y1) %完成插值后的曲线
xlabel('interp1(x,y,x1,''pchip'')','color','b')
legend('y','y1','location','northwest')
title('method = ''pchip''','color','r','fontsize',14)
subplot(2,2,4)
y1 = interp1(x,y,x1,'spline'); %插值函数interp1:计算出这些插值点在y方向上的值存入y1中,y1很长
plot(x,y,x1,y1) %完成插值后的曲线
xlabel('interp1(x,y,x1,''spline'')','color','b')
legend('y','y1','location','northwest')
title('method = ''spline''','color','r','fontsize',14)
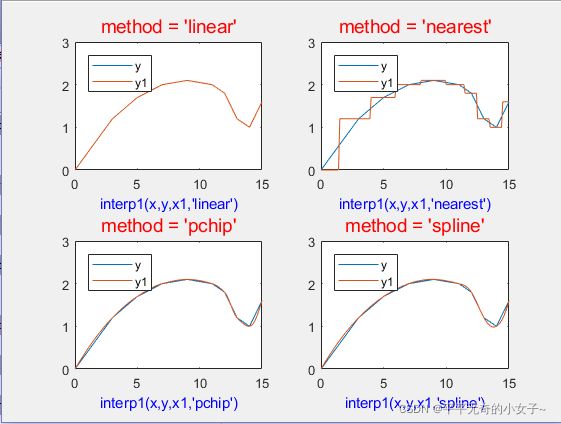
四种方法的比较:
（1）线性插值和最近点插值方法比较简单。其中线性插值方法的计算量与样本点n无关。n越大，误差越小。
（2）3次埃尔米特插值和3次样条插值都能保证曲线的光滑性。相比较而言,3次埃尔米特插值具有保形性;而3次样条插值要求其二阶导数也连续,所以插值函数的性态更好。
（2）interp2():二维插值函数。调用格式:
Z1=interp2(X,Y,Z,X1,Y1,method)
其中，X、Y是两个向量，表示两个参数的采样点,Z是采样点对应的函数值。X1、YI是两个标量或向量，表示要插值的点。method与一维插值方法相同，但不支持pchip方法。
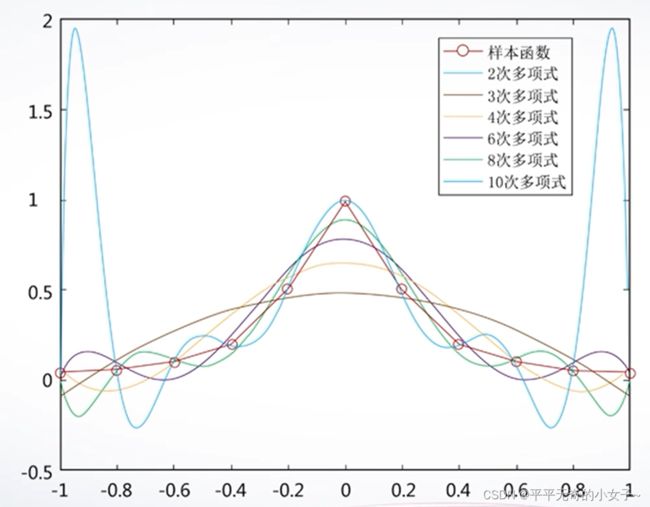
为什么这两种插值方法都用3次多项式而不用更高次的?
答：多项式次数并非越高越好。次数越高，越容易产生震荡而偏离原函数,这种现象称为龙格（Runge)现象。
