MATLAB-插值算法汇总

前言

        数模比赛中常常需要对数据进行分析，当数据不足时就需要补充数据，所用到的方法就是插值法。本文汇总了一些常用的插值算法。

Hermite插值

        埃尔米特插值(Hermite)会在给定的节点处，要求插值多项式的函数值与原函数值相同，同时还要求在节点处，插值多项式的一阶直至指定阶的导数值，也与被插函数的相应阶导数值相等。         Hermite插值在不同的节点，提出的差值条件个数可以不同，若在某节点 ，要求插值函数多项式的函数值，一阶导数值，直至阶导数值均与被插函数的函数值相同及相应的导数值相等。

        详细说明见链接：https://www.docin.com/p-1060241911.html

        直接使用埃尔米特插值得到的多项式次数较高，也存在龙格现象，因此在实际应用中，往往使用分段三次埃尔米特插值

        实现此算法可直接调用matlab中的pchip函数

        代码实现：

    clc;clear;
    x=-pi:pi;
    y=sin(x);                     %以正弦函数为例
    new_x=-pi:0.01:pi;
    p=pchip(x,y,new_x);           %调用pchip函数
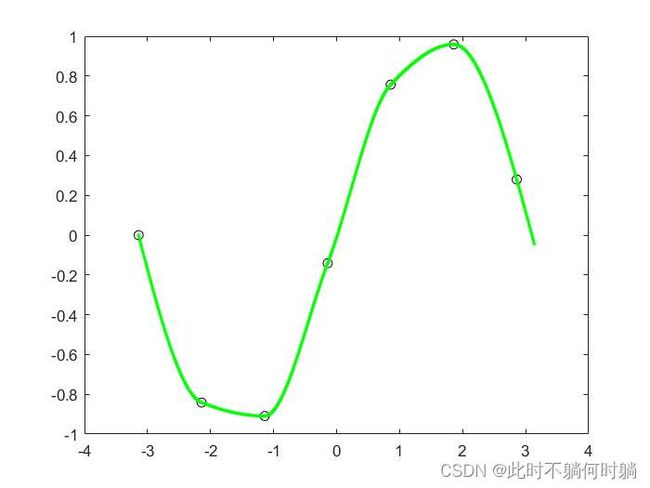
    plot(x,y,'ko',new_x,p,'g.');  %画小圆圈和点

        运行结果如下：

三次样条插值

        三次样条插值（Cubic Spline Interpolation）简称Spline插值，是通过一系列形值点的一条光滑曲线，数学上通过求解三弯矩方程组得出曲线函数组的过程。

        详细证明过程可看链接：https://www.docin.com/p-1391516694.html

         实现此算法可直接调用matlab中的spline函数

        代码实现：

    clc;clear;
    x=-pi:pi;
    y=sin(x);                     %以正弦为例
    new_x=-pi:0.01:pi;
    p=spline(x,y,new_x);          %调用spline函数
    plot(x,y,'ko',new_x,p,'r.');  %画小圆圈和点

        运行结果：

应用

        插值算法不仅可以用来补充数据，也可以用来预测数据，反映趋势等等。

        例如：

clc;clear;
x1=1:10;
y1=[2637	2639	2643	2634	2640	2644	2613	2606	2605	2604];
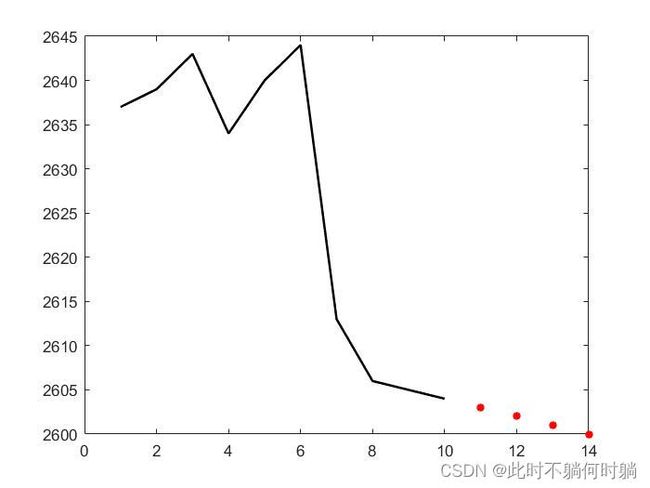
p1=pchip(x1,y1,11:14);      %这里以pchip函数为例
plot(x1,y1,'k-',11:14,p1,'r*','LineWidth',1.5,'MarkerSize',5);  %设置线性和标记

        运行结果如下：