OI学习笔记之数据结构——树状数组

树状数组复杂度 O(logn).
树状数组是一种维护前缀和，区间最大值，区间最小值，区间异或和等满足交换律的东西的数据结构，其支持单点修改和区间查询。
树状数组其实并不算一棵树，它是由数组+二进制的操作实现的，只是在实现的过程中我们借助了树形结构的思想，因此树状数组并不需要建树等操作。
一，认识树状数组

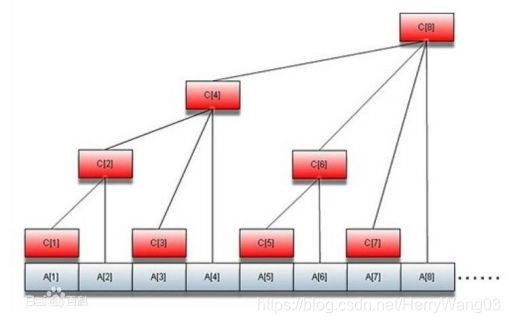
树状数组也是一棵二叉树，长相类似于一棵偏沉的线段树，其中最下面一排数组a代表给定的序列a1,a2…an,c1,c2…为节点编号，其中每个c都维护着若干个连续的a数组的最大值或和或最小值等，那么具体每个节点维护几个a数组呢？是编号是几就维护几个吗？从图中来看，显然不是。
仔细分析树状数组的结构，我们发现c[1],维护的是一个元素a[1],c[2]维护着两个元素a[1],a[2],c[4]维护着四个元素a[1],a[2],a[3],a[4]…
C[1] = A[1];
C[2] = A[1] + A[2];
C[3] = A[3];
C[4] = A[1] + A[2] + A[3] + A[4];
C[5] = A[5];
C[6] = A[5] + A[6];
C[7] = A[7];
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
我们发现每个树节点维护的节点个数都是2^k 个。那么如何求到底是多少呢，就是如何求2^k 的值呢，再仔细分析发现，1的二进制表示是000001，它维护的是2^0 个元素，2的二进制表示是0000010，它维护的是2^1 个元素…，我们发现对于第i号元素维护的数组a的个数就是2^k个（其中k等于其二进制表示末尾零的个数）
C[1] = A[1]; (1:000001)
C[2] = A[1] + A[2];(2:0000010)
C[3] = A[3];(3:0000011)
C[4] = A[1] + A[2] + A[3] + A[4];(4:00000100)
C[5] = A[5];(5:00000101)
C[6] = A[5] + A[6];(6:00000110)
C[7] = A[7];(7:00000111)
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];(8:00001000)

那么如何快速求出2^k的值呢，每次都把它转化成二进制再枚举末尾零的个数么，显然有点慢，也很麻烦QWQ.
为此，我们引入一个叫做lowbit的神奇操作，使得 第i号元素所维护的个数是lowbit(i)个，即对于第i号元素2^{k=lowbit(i),(*注意是2}k=lowbit(i),不是k=lowbit(i)!)下面我们来详解一下lowbit;
Lowbit(x)= x & (-x) ; //背过就好qwq
这里利用的负数的存储特性，负数是以补码存储的，对于整数运算 x&(-x)有
当x为0时，即 0 & 0，结果为0；
当x为奇数时，最后一个比特位为1，取反加1没有进位，故x和-x除最后一位外前面的位正好相反，按位与结果为0。结果为1。
当x为偶数，且为2的m次方时，x的二进制表示中只有一位是1（从右往左的第m+1位），其右边有m位0，故x取反加1后，从右到左第有m个0，第m+1位及其左边全是1。这样，x& (-x) 得到的就是x。
当x为偶数，却不为2的m次方的形式时，可以写作x= y * (2^k )。其中，y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时，x的二进制表示最右边有k个0，从右往左第k+1位为1。当对x取反时，最右边的k位0变成1，第k+1位变为0；再加1，最右边的k位就又变成了0，第k+1位因为进位的关系变成了1。左边的位因为没有进位，正好和x原来对应的位上的值相反。二者按位与，得到：第k+1位上为1，左边右边都为0。结果为2^k。
总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。
//如果看不懂真的背过就好QWQ

二，树状数组的基础操作
1，单点修改：
如果我们想修改数列{a}的某个值怎么办呢？比如我们想修改a[1]。

我们再仔细观察一下这张图，会发现，如果修改a[1]，只会对c[1],c[2],c[4],c[8]产生影响，就是其父节点，父节点的父节点…一直到树根…，所以我们只需要修改被影响节点的值，其他不被影响的节点的值不需要被修改，但树状数组是一种类似于树结构的数据结构，真实操作过程中运用了树的思想，但并没有建树等操作。那我们怎么查找叶子节点并一路修改至根节点呢，我们发现叶子节点就是我们要修改的a[i]，它的第一个父节点一定是c[i],这个…没什么好解释的，c[i]的父节点是c[i]+lowbit（i）,仔细发现下…我们发现每个c节点加上其维护的a节点的数量，就是其父节点的编号，这是树状数组的一个基本性质，其维护a节点的数量在前文已经说过是lowbit(x)。

Code:
inline void update(int k,int v)
{
     While(k<=n)
     {
         tree[k]+=v;
         k+=lowbit(k);
      }
}

2,区间查询
树状数组也可以支持区间查询，因为树状数组维护的是前缀和，所以在进行区间查询的时候，比如查询[x,y]的区间和时，我们要做一次减法，用前y个数的和减去，前x-1个数的和就是[x,y]区间的和，那我们应该怎样求前y个数的和呢，前y个数的和难道是tree[k]吗，显然不是，因为tree[k]维护的是lowbit（k)个数的和,比如tree[3]=a[3]，并不等于a[1]+a[2]+a[3]。

再回到这张图，我们发现前七个数的和等于tree[7]+tree[6]+tree[4],所以我们只要从大到小枚举，每次给x减去lowbit(x)就能算出前x项，不理解可以举几个数手推一下

Code：

inline void getsum(int x)
{
     while(x>0)
     { 
         ans+=tree[x];
         x-=lowbit(x);
     }
}

最后附上树状数组完整代码：

#include
#include
#include
#include

using namespace std;

typedef long long ll;
ll tree[2333],n,m;

inline int lowbit(int x)
{
	return x & (-x);
}

inline void update(int x,int v)
{
	while(x<=n)
	{
		tree[x]+=v;
		x+=lowbit(x);
	}
	return;
}

inline ll getsum(int x)
{
	ll ans=0;
	while(x>0)
	{
		ans+=tree[x];
		x-=lowbit(x);
	}
	return ans;
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		int v;
		scanf("%d",&v);
		update(i,v); 
	}
	for(int i=1;i<=m;i++)
	{
		int q;
		scanf("%d",&q);
		if(q==1)
		{
			int x,v;
			scanf("%d%d",&x,&v);
			update(x,v);
		}
		else
		{
			int x,y;
			scanf("%d%d",&x,&y);
			printf("%lld\n",getsum(y)-getsum(x-1));
		}
	}
	return 0;
}