高级数据结构——树状数组原理和实现

高级数据结构

1.树状数组

树状数组（Binary Indexed Tree，BIT）能够高效地求序列区间和。树状数组的实现简单，巧妙运用了二进制思想。

1.1树状数组的定义

给定一个数组进行两个操作：一是更新某点的值；二是求某段区间的和。对于普通的数组单点更新得复杂度为O(1)，求区间和的复杂度O(n)，而树状数组能够把单点更新和区间求和的复杂度变为
$$O(nlo{g}_n)\text{\hspace{1em}(1)}$$
实现的情况如下图所示：

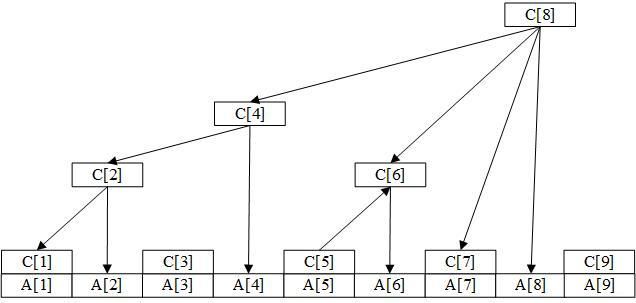
数组A[ ]为原数组，定义：
$$C[i]=A[i-2^k+1]+...+A[i]\text{\hspace{1em}(2)}$$

$$k为用二进制表示数的0的个数，如C[1]=A[1]，C[2]=A[1]+A[2],...即C[i]就是从A[i]开始前2^k项的和$$

1.2树状数组的实现和使用

k为x用二进制表示时末尾0的个数，对于2^k,有一种快速求解的方法：

int lowbit(int x){
    return x &(-x);
}

当修改某一点的值得时候只需要修改某一点所有的父节点就可以了，对一个节点i来说，它的父节点的编号为i+lowbit（i）。因此对于单点修改的函数为

//在position处加value，len是数组长度
void change(int c[],int position,int value,int len){
      while(position<=len){
          c[position]+=value;
          position+=lowbit(position);
      }
}

前n个数和记sum（n），已知C[i]是从i开始向前lowbit（i）个数的和，所以sum(n)=C[n]+sum[n-lowbit(n)]。

// 求前n个数的和
int sum(int c[],int n){
    int answer=0;
    while(n>0){
        answer+=c[n];
        n-=lowbit(n);
    }
    return answer;
}

1.3例题讲解

给定一个由n个不同的整数组成的序列，通过交换相邻的两个数，使得序列变成上升的。问最少需要交换多少次，如“1 2 3 5 4”，需要进行一次操作，交换5和4.

输入：

//包括多组数据，每一组数据包含两行，第一行为一个正整数n(n<1000),第二行为从1到n的n个整数的一个序列。

输出：

输出为1行，输出最少需要交换的次数。
样例输入：

3

1 2 3

4

4 3 2 1
样例输出：
0
6
题目来源：HDOJ 2689.
解题思路：
题目可以转化为求数组中逆序对的数量。

执行（C++）代码如下：

#include 
#include 
using namespace std;

const int N=1000;

int lowbit(int x){
    return x& (-x);
}

//在position处加value，len是数组长度
void change(int c[],int position,int value,int len){
      while(position<=len){
          c[position]+=value;
          position+=lowbit(position);
      }
}

// 求前n个数的和
int sum(int c[],int n){
    int answer=0;
    while(n>0){
        answer+=c[n];
        n-=lowbit(n);
    }
    return answer;
}

int main()
{
    int n;
    int c[N];						//树状数组
    while(~scanf("%d",&n)){			//序列包含多少个数字
        memset(c,0,sizeof(c));
        int x;
        int answer=0;
        for (int i=1;i<=n;++i){
            scanf("%d",&x);			//读入每一个数字
            change(c,x,1,n);		//在树状数组x处加1
            answer+=i-sum(c,x);		//把每一个数字的贡献相加			
        }
        printf("%d\n",answer);
    }
    return 0;
}