matlab自学笔记
目录
变量命名
清空环境变量及命令
变量命名规则
添加注释
数据类型
数字运算
字符与字符串
矩阵
元胞数组
结构体
矩阵操作
矩阵的定义与构造
矩阵的四则运算
矩阵的下标
matlab逻辑与流程控制
结构
顺序结构
循环结构
分支结构
matlab基本绘图操作
二维平面绘图
三维立体绘图
变量命名
清空环境变量及命令
- clear all :清除Workspace中所有变量
- clc :清除Command Window中所有命令
变量命名规则
区分大小写、长度不超过63位、字母开头
添加注释
% 注释一行
%% 代码分块执行
数据类型
数字运算
+-*/
字符与字符串
- str=‘a’(命名)
- num2str(65):数字转字符串
- abs(str):字符串转ASCII码
- char(str)
- length(str):计算字符串长度
矩阵
矩阵基础
| 矩阵命名 |
A =[1 2 3; 4 5 7; 2 7 9] |
| 求矩阵的转置 |
B =A' |
| A矩阵竖向拉伸 |
C =A(:) |
| 求矩阵的逆 |
D =inv(A) 要求必须是方阵! |
- E = zeros(10,5,3) 创建一个10行5列的三维数组
- E(:,:,1) 一维
- E(:,:,2) 二维
- E(:,:,3) 三维
注意:1.matlab中下标从1开始!
2.matlab中存储矩阵是按列存储的
随机数(rand、randi、randn)
1.rand 生成均匀分布的伪随机数。分布在(0~1)之间
主要语法:
- rand (m,n) 生成m行n列的均匀分布的伪随机数
- rand (m,n,'double') 生成指定精度的均匀分布的伪随机数,参数还可以是'single'
- rand (RandStream,m,n) 利用指定的RandStream(随机种子)生成伪随机数
2.randn 生成标准正态分布的伪随机数(均值为0.方差为1)
主要语法:同上
3.randi 生成均匀分布的伪随机整数
主要语法:
- randi (iMax) 在开区间(0,iMax)生成均匀分布的伪随机整数
- randi (iMax,m,n) 在开区间(0,iMax)生成mXn型随机矩阵
- r = randi ([iMin,iMax],m,n) 在开区间(iMin,iMax)生成mXn型随机矩阵
元胞数组
元胞数组是MATLAB中特有的一种数据类型,是数组的一种,其内部元素可以是属于不同的数据类型,概念理解上,可以认为它和c语言里面的结构体、c++里面的对象很类似。元胞数组是matlab中的特色数据类型,它不同于其它数据类型 (如字符型,字符数组或者叫字符串,以及一般的算术数据和数组) 。它特有的存取数据方法决定了它的特点,它有给人一种查询信息的感觉,可以逐渐追踪一直到所有的变量全部翻译成基本的数据信息。它的class函数输出就是cell (细胞之意) 。
A = cell(1,6) 定义一个1行6列的元胞数组
A{2} = eye(3) 将eye(3)赋值给A数组的第二个框
注释 :1. eye生成一个3*3的对角线为1的单位矩阵
2. matlab索引从1开始
A{5} = magic(5) 将magic(5)赋值给A数组的第五个框
注释:magic字面意思是魔方,魔术的意思。在matlab中用来生成n阶幻方。比如三阶幻方就是1-9九个数字,组成一个3*3的矩阵,使得该矩阵无论横、竖还是斜三个方向上的三个数的和总是相同的。magic(n)生成一个n阶幻方,就是把1-nA2排成一个nxn的矩阵,使得矩阵的每行每列,以及主、副对角线上面的n个数之和都相等(容易证明,这个和等于n*(n^2+1)/2)
结构体
命名:books = struct(‘name’,{{‘Machine Learning’,‘Data Mining’}},‘price’,[30,40])
books =
包含以下字段的 struct:
name: {'Machine L' 'Data'}
price: [30 40]
books.name 属性
1×2 cell 数组
{'Machine L'} {'Data'}
books.name(1)
1×1 cell 数组
{'Machine L'}
books.name{1} 输出的是字符串
'Machine L'
矩阵操作
矩阵的定义与构造
A = [1 2 3 4 5 6 7 8] 定义
A =
1 2 3 4 5 6 7 8
B = 1:2:9 1——起始,2——步长,9——终点(不可缺少任一项!!)
B =
1 3 5 7 9
C = repmat(B,3,2) 将B矩阵重复3行2列
C =
1 3 5 7 9 1 3 5 7 9
1 3 5 7 9 1 3 5 7 9
1 3 5 7 9 1 3 5 7 9
D = ones(2,4) 生成一个全是1的2行4列矩阵
D =
1 1 1 1
1 1 1 1
矩阵的四则运算
A = [1 2 3 4; 5 6 7 8]
A =
1 2 3 4
5 6 7 8
B = [1 1 2 2; 2 2 1 1]
B =
1 1 2 2
2 2 1 1
C = A + B
C =
2 3 5 6 一一对应相加
7 8 8 9
D = A - B
D =
0 1 1 2 一一对应相减
3 4 6 7
E = A * B' B' B的转置,B的行数要与A的列数相同
E =
17 13 A乘B的转置
41 37
F = A.* B 加 ' . ' 的意思是对应项相乘
F =
1 2 6 8 AB中对应项相乘
10 12 7 8
G = A \ B %% G * B = A ,G * B * pinv(B)= A * pinv(B) ,G = A * pinv(B)
G =
1.8333 -0.1667 A乘B的逆
3.1667 1.1667注释:pinv 与 inv
1.对于方阵A,如果为非奇异方阵,则存在逆矩阵inv(A)
2.对于奇异矩阵或者非方阵,并不存在逆矩阵,但可以使用pinv(A)求其伪逆
若A为非奇异矩阵,请不要使用pinv求逆,虽然计算结果相同,即
inv( A ) = pinv( A )
但pinv的计算复杂度较高。
H = A.\ B
H =
1.0000 2.0000 1.5000 2.0000 对应项相除
2.5000 3.0000 7.0000 8.0000
矩阵的下标
A = magic(5) 5*5的幻方矩阵
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
B = A(2,3) 取A的第2行第3列元素
B =
7
C = A(3,:) 取A的第3行
C =
4 6 13 20 22
D = A(:,4) 取A的第4列
D =
8
14
20
21
2
[m,n] = find(A > 20) %%找大于20的序号值/矩阵
m =
2
1
5
4
3
n =1
2
3
4
5
注释:find()函数
- find()函数的功能是找到向量或者矩阵中不为0的元素,还可以找到满足某些条件的元素
- 如何使用find函数返回矩阵或向量中非零元素的索引? find(vector)
- 如何使用find函数返回向量中前k个非零元素的下标? find(vector,k)或find(vector,k,'first')
- 如何使用find函数返回向量中后k个非零元素的下标? find(vector,k,'last')
- 如何使用find函数返回矩阵中非零元素的行号与列号? 见如下注释1
- 如何使用find函数找到向量或矩阵中满足特定条件的元素? 见如下注释2
%%vector是向量名称,如x,y等
注释1:返回行号与列号与值
x = [1 2 3; 4 5 6; 7 8 9]
[r,c] = find(x)
[r,c,v] = find(x)[r,c,v]
ans =
1 1 1
2 1 4
3 1 7
1 2 2
2 2 5
3 2 8
1 3 3
2 3 6
3 3 9
注释2:进阶用法
x=[1 2 3 4 5 6 7 8 9]
- find(x>=5)
- find(x==4)
- ~isempty(find(3)) 判断向量中是否含有某个元素
ans
= logical 1 isempty(A) :A为空,返回1 && A非空,返回0
matlab逻辑与流程控制
结构
(所有结构都必须有end!)
顺序结构
一步一步计算
循环结构
1.for循环
for 循环变量 = 初值:步长:终值
执行语句1
.
.
.
执行语句n
end
%%步长默认为1,可以省略
例子:求![]()
>>sum = 0;
>>for n = 1:5
sum = sum + n^2
end
>>sum
sum=
153注意:语句后加 ' ; ' 可以起到只显示语句但不执行的作用
2.while循环
while 条件表达式
执行语句1
.
.
.
执行语句n
end
例子:求 1+2+3+4+...+10
>> s = 0;
>> n = 1;
>> while n <=10
s = s + n;
n = n + 1;
end
>> s
s =
55分支结构
1.if...end 结构
if 条件表达式 %%条件表达式为真,执行语句体;为假,跳出循环
.
.
.
语句体
.
.
.
end
例子:
>> clear all
>> a = 100;
>> b = 20;
>> if a>b
'成立'
end
ans =
'成立'
2.if...esle...end 结构
if 表达式
语句体1
else
语句体2
end
3.switch...case...and 结构
switch 表达式(数值或字符串)
case数值或字符串1
语句体1;
case数值或字符串2
语句体2;
.
.
.
otherwise %% otherwise可以省略,此时所有case不满足,跳出循环
语句体n;
end
matlab基本绘图操作
二维平面绘图
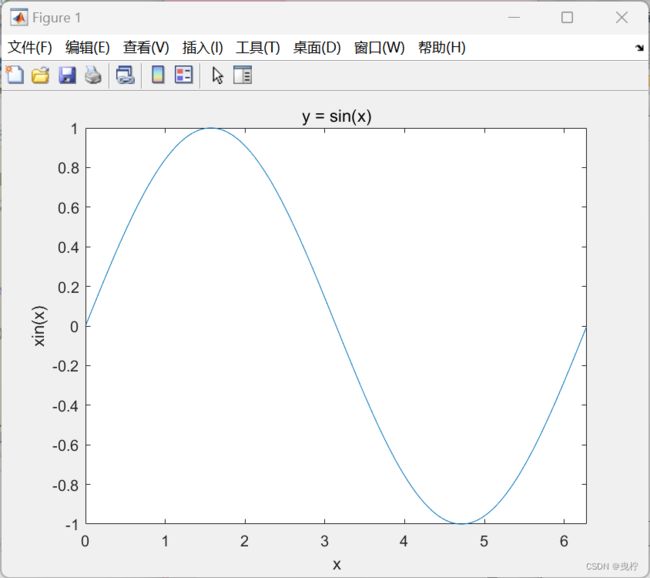
例子1:单函数
x = 0:0.01:2*pi;
y = sin(x);
figure %%建立幕布
plot(x,y)
title('y = sin(x)') 图像命名
xlabel('x') x轴命名
ylabel('xin(x)')
xlim([0 2*pi]) 将幕布中显示的x轴的范围定义在 [0,2pi] 之间
PS:matlab参数表
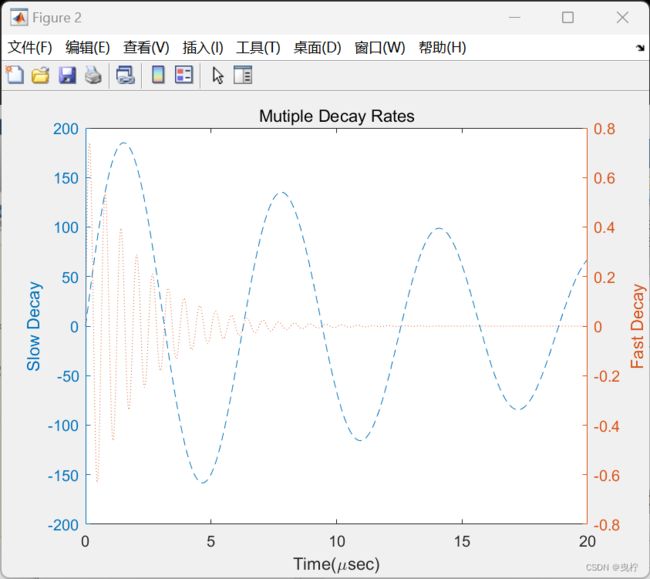
例子2:双函数
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
figure
[AX,H1,H2] = plotyy(x,y1,x,y2,'plot'); %%建立一个x两个y的函数图
set(get(AX(1),'Ylabel'),'String','Slow Decay')
set(get(AX(2),'Ylabel'),'String','Fast Decay')
xlabel('Time(\musec)')
title('Mutiple Decay Rates')
set(H1,'LineStyle','--') %%用虚线绘制
set(H2,'LineStyle',':') %%用点线绘制
注释1:exp()函数
1、exp函数:求以e为底的指数函数
exp(x) =
2、用法说明:y=exp(x) 函数对数组元素x进行逐个处理的函数。函数定义域包括复数。对于复数z=a+b*i,有ez=(cos(b)+i*sin(b)*ea)
注释2:set()函数
1、set函数用于设置图形对象的属性
2、属性的操作
set函数的调用格式为:
set(句柄,属性名1,属性值1,属性名2,属性值2,…)
set(handle, 'PropertyName', PropertyValue)
handle是要修改属性的图形对象的句柄,'PropertyName’是要修改的属性名称,PropertyValue是要为该属性设置的新值。
注释3:get()函数
get()函数是用来获取图形、UI及特定对象的属性值的函数
三维立体绘图
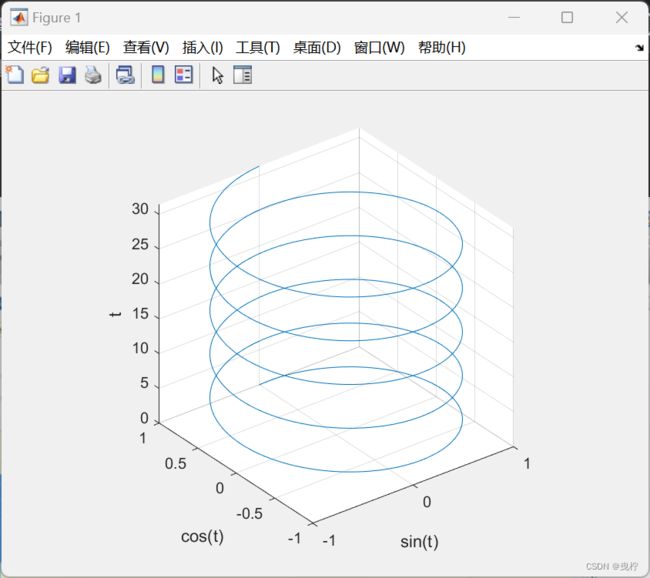
例子1:
t = 0:pi/50:10*pi;
plot3(sin(t),cos(t),t) 建立三维图像
xlabel('sin(t)')
ylabel('cos(t)')
zlabel('t')
grid on %%在图像中加入网格线
axis square %%调整图像纵横比为1:1