【文献笔记】测风激光雷达控制系统的研制与风场观测
文章来源:测风激光雷达控制系统的研制与风场观测 中国科学技术大学 周安然 博士论文 2020.06测风激光雷达控制系统的研制与风场观测 - 中国知网 (cnki.net)
风场探测的研究意义
测风激光雷达作为一种高时空分辨率的风场探测手段,其在航空安全保障领域受到了广泛的关注并在部分机场取得了应用。
风力发电厂需要精准的实时风场信息用以优化风力发电机组的位置,提高风力发电效率。
风力发电作为一种新能源,同样有着可再生、无污染、排放的特点,但缺点在于风力资源不可控,且资源分布差异大。为了合理选择建立风力发电场的位置,需要对地区长期的风场有准确掌握。
风力发电厂主要由大量风轮组成,将风的动能转化为电能。可以看出无论是建在陆地还是建在海上的风力发电厂,适合采用大气风场遥感探测的方法找出整片区域中风速合适的位置。在选址完成后,还需要决定风轮的密度。如果密度过低,难以充分利用整片风场的资源;而如果密度过高,风在经过风轮后的尾流会延伸一定的长度,之后逐渐扩展耗散。尾流区域风速弱于周边风场且存在较强的湍流,将会降低接触到的后方风轮的发电效率和使用寿命。
由于风轮尾流和当地的地形起伏、风场及风轮大小都有关系,为了每个精确的测定风轮尾流的长度和扩散范围,同样需要能精确的测量大片实时风场。目前激光测风雷达也在风机部署间隔的优化这方面取得了应用。
风场探测的主要方法
常用方法包括:超声波风速仪、多普勒雷达、无线电探空仪和测风激光雷达
超声波风速仪测量结果精度高,时间分辨率也高且运行稳定可以在无人值守的环境下长期测量并输出数据。广泛应用与气象局测风塔、机场以及风电等领域。但超声波风速仪在空间上只能测量一点的风场,无法掌握整个风场动态。
多普勒雷达和激光测风雷达的基本原理相似:通过测量被测目标的多普勒频移计算目标的朝向或远离的速度。不同之处在于多普勒雷达工作在微波波段,其发射的波长大于100 um,无法得到气溶胶米散射信号。因此多普勒雷达主要测量对象是大气中的沙尘、云、雨和雾等。对于测量大气风场只能根据这几种测量目标的速度间接推测出大气风速,且要去除复杂环境中的杂波干扰如昆虫群、鸟雀等的反射信号才能保证测量结果的可靠性。可以看出在晴空条件下,激光雷达的表现较好而微波雷达的信号很微弱。而在雾霾、阴雨和扬尘天气下激光雷达的信号会迅速衰减,表现不如微波雷达。两种大气风场探测手段性能互补无法相互取代。目前多普勒雷达在大气遥感的应用主要集中于气象探测。
无线电探空仪是搭载在氢气球上,通过气球坐标的变化求出气球的速度作为风场信息。由于气球在水平风向上的移动量不能完全反应出所在风场的风速大小,且当风向改变时气球由于惯性,速度变化存在滞后可以看出这种方法对风速测量的精度较前两种方法较低。此外由于不能保证回收这种探空仪使用是一次性的,因此不能长时间连续获取风场信息。
激光测风雷达主要基于现代激光器技术,通过向大气发出窄线宽的激光与大气粒子相互作用,接收带有多普勒频移信息的大气散射光。多种多样的测风激光雷达可以满足不同的风场探测需要,无论是高时间分辨率的边界层风场还是高至大气非常稀薄的平流层风场都可以提供长时间准确的风场数据。目前测风激光雷达已经应用在气象、航空航天、风能等领域取得了应用。
非相干测风激光雷达原理
多普勒效应
几乎所有风廓线测量系统都使用多普勒频移获取径向风速。对于激光雷达,发射的激光束在传播中被大气中的分子及气溶胶粒子散射,一部分散射光回到激光雷达的接收系统,作为大气回波信号被接收机收集。大气粒子的移动速度对散射光造成了频率上的移动,被称为多普勒频移。当大气粒子朝向雷达系统移动时,其反射出的后向散射光频率将会增加,这也被称为“蓝移”,反之远离雷达系统移动时将会造成“红移”。多普勒频移的大小与风速大小线性相关,可以通过出射光与接收光频率的差值,得到大气风速信息。
多普勒频移的大小不只取决于风速,也受风速矢量在激光雷达望远镜视向上的分量影响。如图所示,激光雷达系统发射出中心频率为 v 0 v_0 v0的窄带激光到大气中,与风速为 V V V的大气粒子发生作用,产生中心频率为 v 1 v_1 v1的散射光,风矢量与望远镜朝向的夹角为 θ \theta θ,则视向风速可由下式计算:
V r = − λ ( v 1 − v 0 ) / 2 V_r=-\lambda(v_1-v_0)/2 Vr=−λ(v1−v0)/2
v r v_r vr为沿着望远镜径向的风速分量, λ \lambda λ为发射激光的中心波长, v 1 − v 0 v_1-v_0 v1−v0的结果即为大气后向散射光与发射激光之间的多普勒频移量。
频率的检测
为了获取回波信号的多普勒频移量,需要有专门的鉴频设备,鉴频器不是直接测量发射光与接收光的频率,而是根据其接收光通过鉴频设备前后的强度变化,以及鉴频器自身的对不同频率光的吸收或透过率曲线计算出频移量。
通过测量大气散射光的强度在空间上的分布变化来确定频移量的方法被称为条纹成像技术,其鉴频设备可以是法布里-珀罗干涉仪、菲索干涉仪和马赫-曾德尔干涉仪等。而通过测量经过鉴频设备后光强度变化来确定频移量的方法被称为边缘技术。边缘技术按使用的鉴频设备主要包括分子吸收谱线和法布里-珀罗标准具。
最初的边缘技术主要利用一个鉴频设备,将测量的激光频率定在该鉴频设备透过率谱线斜率较大的位置上。这样散射光在经过鉴频设备后的透过率相比出射光产生较大的变化,通过透过率的相对变化量确定散射光的频移量。这种边缘技术被称为单边缘技术。而在此基础上发展出了双边缘技术,已被证明有着更好的性能,是目前国际上多普勒激光雷达系统取得了很多应用。
为了突出多普勒频率变化引起的通过光强变化,将两个边缘通道通过的光强相减后除以相加得到响应函数 R ( v , z ) R(v,z) R(v,z),计算公式为:
R ( v , z ) = T Ray 1 ( v , z ) − T Ray 2 ( v , z ) T Ray 1 ( v , z ) + T Ray 2 ( v , z ) R(v, z)=\frac{T_{\text {Ray } 1}(v, z)-T_{\text {Ray } 2}(v, z)}{T_{\text {Ray } 1}(v, z)+T_{\text {Ray } 2}(v, z)} R(v,z)=TRay 1(v,z)+TRay 2(v,z)TRay 1(v,z)−TRay 2(v,z)
其中 T R a y 1 ( v , z ) T_{Ray1}(v,z) TRay1(v,z)和 T R a y 2 ( v , z ) T_{Ray2}(v,z) TRay2(v,z)分别为高度 z z z处中心频率为 v v v的大气分子散射信号经过标准具边缘通道后的强度。每个高度的响应值可以从采集结果中计算,确定了响应值后对应的频率还需要确定响应函数 R ( v , z ) R(v,z) R(v,z)。
由于经过标准具后的信号强度为瑞利谱与标准具通过率曲线的卷积,R(z)可以在开始测量前通过计算求得。为了计算响应函数值,首先标准具的透过率曲线为:
T ( v ) = T p [ 1 + 4 R ( 1 − R ) 2 sin 2 ( 2 π n L cos θ / λ ) ] − 1 T(v)=T_p\left[1+\frac{4 R}{(1-R)^2} \sin ^2(2 \pi n L \cos \theta / \lambda)\right]^{-1} T(v)=Tp[1+(1−R)24Rsin2(2πnLcosθ/λ)]−1
其中, v v v为入射光频率; θ \theta θ是入射光与标准具反射镜面法线的夹角; R R R是标准具平面反射率; n n n为平面镜之间的折射率; L L L是标准具谐振腔腔长; λ \lambda λ是入射光波长; T p T_p Tp是标准具的峰值透过率。实际加工中镜面总是会存在缺陷不能达到理想平面,用有效反射率 R e R_e Re替代反射率 R R R,定义 F e = π R e / ( 1 − R e ) F_e=\pi\sqrt{R_e}/(1-R_e) Fe=πRe/(1−Re)为有效精细度,可以得到:
T ( v ) = T p [ 1 + 4 F e 2 π 2 sin 2 ( 2 π n L cos θ / λ ) ] − 1 T(v)=T_p\left[1+\frac{4 F_e^2}{\pi^2} \sin ^2(2 \pi n L \cos \theta / \lambda)\right]^{-1} T(v)=Tp[1+π24Fe2sin2(2πnLcosθ/λ)]−1
由于入射到标准具的光束在实际实验中经过透镜准直入射不会是完全垂直入射而是存在一定的发散角,光束发散件很小的情况下,透过率可以近似表示为:
T ( v ) = 2 θ 0 2 ∫ 0 θ 0 h ( v ) ⋅ sin θ d θ = 2 θ 0 2 ∫ 0 θ 0 T p e 1 + 4 F e 2 π 2 sin 2 ( π v cos θ / Δ v F S R ) ⋅ sin θ d θ T(v)=\frac{2}{\theta_0^2} \int_0^{\theta_0} h(v) \cdot \sin \theta d \theta=\frac{2}{\theta_0^2} \int_0^{\theta_0} \frac{T_{p e}}{1+\frac{4 F_e^2}{\pi^2} \sin ^2\left(\pi v \cos \theta / \Delta v_{F S R}\right)} \cdot \sin \theta d \theta T(v)=θ022∫0θ0h(v)⋅sinθdθ=θ022∫0θ01+π24Fe2sin2(πvcosθ/ΔvFSR)Tpe⋅sinθdθ
为了便于计算机编程计算,需要将上式展开成级数相加的形式
T ( v ) = T p e ( 1 − R e 1 + R e ) { 1 + 2 ∑ n = 1 + ∞ R e n cos ( 2 π n v Δ v F S R ⋅ 1 + cos θ 0 2 ) sinc ( 2 n v 0 Δ v F S R ⋅ 1 − cos θ 0 2 ) } T(v)=T_{p e}\left(\frac{1-R_e}{1+R_e}\right)\left\{1+2 \sum_{n=1}^{+\infty} R_e^n \cos \left(\frac{2 \pi n v}{\Delta v_{F S R}} \cdot \frac{1+\cos \theta_0}{2}\right) \operatorname{sinc}\left(\frac{2 n v_0}{\Delta v_{F S R}} \cdot \frac{1-\cos \theta_0}{2}\right)\right\} T(v)=Tpe(1+Re1−Re){1+2n=1∑+∞Rencos(ΔvFSR2πnv⋅21+cosθ0)sinc(ΔvFSR2nv0⋅21−cosθ0)}
对于大气分子后向散射光谱 I R a y ( v ) I_{Ray}(v) IRay(v),由于其相对于发射光谱受大气分子热运动的影响,与温度有关,可以用高斯函数的形式表示为:
I R a y ( v ) = 1 π Δ v R e ( v 2 Δ v R 2 ) I_{R a y}(v)=\frac{1}{\sqrt{\pi} \Delta v_R} e^{\left(\frac{v^2}{\Delta v_R^2}\right)} IRay(v)=πΔvR1e(ΔvR2v2)
其中, Δ v R \Delta v_R ΔvR分别为分子后向散射谱的1/e半宽,其公式为:
Δ v R = 32 k T / λ M \Delta v_R=\sqrt{32 \mathrm{kT} / \lambda \mathrm{M}} ΔvR=32kT/λM
其中 k k k是玻尔兹曼常数, T T T是大气温度一般带入随高度变化模式温度数据计算, λ \lambda λ是激光波长, M M M是单个空气分子的平均质量。最后,可以得到不同中心频率的大气分子回波信号经过标准具的透过率。
T R a y ( v ) = T p e ( 1 − R e 1 + R e ) ⋅ { 1 + 2 ∑ n = 1 + ∞ R e n cos ( 2 π n v Δ v F S R ⋅ 1 + cos θ 0 2 ) ⋅ e − ( π n Δ v F S R ⋅ 1 + cos θ 0 2 ⋅ Δ v R ) 2 ⋅ sinc ( 2 n v 0 Δ v F S R ⋅ 1 − cos θ 0 2 ) } \begin{aligned} T_{R a y}(v)= & T_{p e}\left(\frac{1-R_e}{1+R_e}\right) \cdot\left\{1+2 \sum_{n=1}^{+\infty} R_e^n \cos \left(\frac{2 \pi n v}{\Delta v_{F S R}} \cdot \frac{1+\cos \theta_0}{2}\right) \cdot e^{-\left(\frac{\pi n}{\Delta v_{F S R}} \cdot \frac{1+\cos \theta_0}{2} \cdot \Delta v_R\right)^2}\right. \\ & \left.\cdot \operatorname{sinc}\left(\frac{2 n v_0}{\Delta v_{F S R}} \cdot \frac{1-\cos \theta_0}{2}\right)\right\} \end{aligned} TRay(v)=Tpe(1+Re1−Re)⋅{1+2n=1∑+∞Rencos(ΔvFSR2πnv⋅21+cosθ0)⋅e−(ΔvFSRπn⋅21+cosθ0⋅ΔvR)2⋅sinc(ΔvFSR2nv0⋅21−cosθ0)}
计算出双边缘通道对瑞利信号的透过率曲线后,不同高度下的响应函数 R ( v ) R(v) R(v)就可以通过上面的公式计算。根据实测的信号强度计算出不同高度的响应值,确定其在响应函数上对应的频率,再由风速和频率的公式计算出风速。
数据采集系统
激光雷达数据采集系统主要包括用于光电转化的光电倍增管(PMT)、采集并保存电信号的瞬态记录仪和采集卡。其中光电倍增管受外部门控信号控制输出的开始、关闭,与上位控制机没有接口相连故没有控制软件。而对于采集卡和瞬态记录仪需要分别编写软件控制其开始采集、累积次数以及传回采集结果。
光电倍增管
对于非相干系统望远镜接收的测量高度在40公里乃至更高的散射光信号,会由于往返的衰减、极其稀薄的大气分子等原因变得非常微弱,需要探测器能响应非常微弱的信号且有较低的噪声。同时由于探测距离的跨度非常大,需要光电探测器具有具有较大的动态范围。
当有光入射到PMT的阴极靶面上时,靶面物质由于其光电效应将会跃迁出光电子。光电子在外接高压电场的影响下在PMT的真空腔内加速飞行并冲击到第一个倍增极,倍增极将发出至少两倍的电子,继续在电场中加速前往下一个倍增极。重复几轮后得到倍增前数倍的电子在阳极输出。这样可以将非常微弱的大气散射光信号转化并放大为可以被测量的电信号而且有响应时间短噪声小的优点。
高压输入接口用于接入加速电子所需的高压,其电压强度与PMT的信号增益有关,关系如下:
G = a U b n G=aU^{bn} G=aUbn
其中 G G G为增益,系数 a a a为靶面光电转化性能,系数 b b b为倍增级的响应, n n n为倍增级个数, U U U为所加高压。可以通过提高接入电压来增强增益,但长期高压也可能损伤PMT中的元器件。
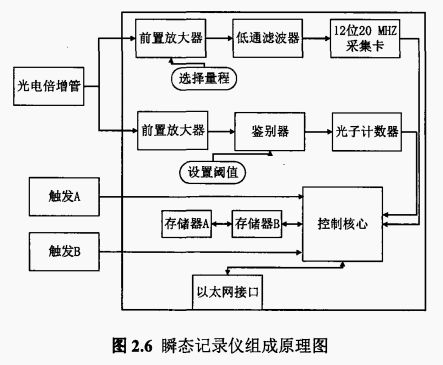
瞬态记录仪
如图2.6所示,瞬态记录仪的内部分为光子采集、模拟探测、数据存储及逻辑控制核心等几部分组成。
为了控制瞬态记录仪,需要与其建立网络连接。这里采用了微软提供的网络接口库 winsock2建立连接。首先需要新建套接字,用于创建维护网络通信设备端到端直接的连接。
采集时由于光子计数模式适用于较低的光强度,而模拟探测模式适用于较高光强度。两种模式的对比见图2.7。在信号弱时,模拟探测是信号引起的电压往往淹没在电子设备带来的电噪声中。在信号强时,光子计数部分可能会更容易出现两个光电子产生的脉冲重叠成一个电脉冲而使得甄别器无法有效鉴别出光子个数,模拟探测由于电压的叠加信噪比提高。
当光信号越强形成的电脉冲越多这种现象就约为明显,这种现象被称为光子计数的死时间。假设光子数的分布服从泊松分布,死时间校准的公式为:
N c = N 1 − N τ N_c=\frac{N}{1-N \tau} Nc=1−NτN
其中 N c N_c Nc为校准后的光子数, N N N为校准前的光子数, τ \tau τ为死时间,死时间受光电子的脉冲宽度、阈值的设置、以及鉴频器的频率有关。