5.1.7_定点小数
文章目录
- 一、介绍
- 二、原反补
- 三、运算
- 四、定点整数和定点小数
- 五、案例
-
- (1)案例一
- (2)案例二
- (3)案例三
一、介绍
这一个小节,我们要学习定点小数的表示和运算。
之前我们学习了整数的表示和运算,分为有符号整数和无符号整数两种。
那么定点小数,这个定点是什么意思?定点的意思就是小数点的位置固定。

我们之前学习的带符号整数,也可以把它称为定点整数。
之前在讲带符号整数的时候,我们其实默认了这样的一个规则。就是在二进制数当中,我们默认了小数点固定在最后位置。
小数点前边这一位,它的位权是 2 的 0 次方,再往前是 2 的1次方, 2 的2次方等等。

所以我们的位权是多大,它是根据这一位和小数点的相对位置来决定的。
所以之前我们学习的带符号整数,又可以把它称为定点整数,我们默认了小数点固定在最后位置。
结合之前学习的内容,我们知道定点整数可以用原码、反码、补码,还有移码这样的 4 种编码来表示。
而对于定点小数来说,我们只能用原码、反码和补码来表示。
计算机内部的定点小数,我们会默认这个小数点隐含在符号位的后面这个位置。

所以这就意味着,当我们确定每个比特位的位权的时候,就得根据这些位和小数点的相对位置关系来确定,小数点后面位置它的位权应该是 2 的- 1 ,接下来是 2 的- 2 次方,以此类推。

所以定点小数和定点整数的区别就在于,我们默认的小数点的隐含位置是不一样的。

二、原反补
- 原码
小数点隐含在符号位后面,那么符号位后边的这些数值部分,它的位权依次是 2 的-1次方、 2 的-2次方,以此类推,这是每1个比特位的位权。

既然是原码,那我们首先根据符号位确定正负性。 0 为正, 1 为负。
所以上面定点小数它的真值应该是 2 的负一次方加上 2 的负二次方,后边都是0,不用管,所以上面定点小数的真值应该是 0. 75。

下面这个定点小数的真值也是一样的。
在书本里边,如果是定点整数,这个符号位的后面通常是用一个小逗号来隔开;定点小数符号位的后面通常是用一个点,就是小数点来隔开。
这是定点小数的原码表示,其实和定点整数的原码都是一样的,只不过我们默认的小数点的位置不一样而已,因此就会导致各个比特位的位权有一些区别。

- 反码和补码
接下来再来看定点小数的反码和补码。怎么从定点小数的原码转换为反码和补码呢,和定点整数一模一样,在这就不再赘述。如下图:

三、运算
接下来我们来说一说定点小数的加减运算怎么实现。
如果要对两个定点小数 A 和 B 进行加法或者减法,运算的时候和定点整数一样,我们需要先把它转为补码,然后对补码进行加减运算。
四、定点整数和定点小数
接下来我们来看一看定点小数和定点整数不一样的地方。
除了默认的小数点位置不一样,以及各个比特位的位权不一样之外,他们的合法的表示范围最大的数,最小的数和真值 0 的表示如下表:

<1> 原码
先看定点小数的原码,它可以表示的合法范围应该是多少。
定点小数的原码,它的数值部分可以表示的最大的值应该是全为 1 ,数值部分全部为1它所对应的真值应该是 2 的- 1 次方加 2 的- 2 次方一直加到 2 的- 7 次方。

如果用表格里边的条件(n+1比特)来说,应该是 2 的- 1 次方,一直加到 2 的- n 次方。这是一个等比数列求和问题,这个等比数列求和应该是 1减去2 的-n 次方。
这就意味着在定点小数的原码当中, n 个比特的数值位可以表示的值应该是 0~1-2 的-n 次方。再结合前边的符号位,可以为正,也可以为负。
因此,定点小数它的表示范围最大就应该是 1- 2 的负 n 次方,最小就应该是负的 1- 2 的负 n 次方。最大的数和最小的数怎么表示这儿就不再赘述。
定点小数对于真值 0 的表示,同样有正 0 和负 0 这样的两种。
<2>反码
接下来定点小数的反码。
反码和原码是一模一样的,所以它的合法的表示范围以及正 0 负 0 有两种真值 0 的表现方式,这些都是一样的。
只不过反码的负数需要在原码的基础上把数值位按取反,这是反码和原码唯一的区别。
<3>补码
最后再来看定点小数的补码。
和定点整数的补码一样,如果用 n 加 1 个比特的补码来表示定点小数,它可以表示的负数的范围要比原码可以表示的负数范围更大。
最小的负数可以表示-1。当符号位为1,后面那些位全部为 0 的时候,补码的真值最小,对应的就是-1。
定点小数的补码,它的真值 0 也只有一种表现形式。
所以学了之前的定点整数,我们再来学定点小数。这些知识其实都是相通的。
在表里边这些小逗号,你可以把它改成点,不过不改也没关系,无伤大雅,大家知道什么意思就行,不用去钻牛角尖。
好的,这是定点小数和定点整数的对比。
接下来我们再看定点小数和定点整数的另一个比较重要的区别。
对于定点小数,如果把 4 比特的定点小数扩展为 8 比特的定点小数,由于我们这个小数点是固定在符号位的后面这个位置,所以我们要扩展的这 8 个比特,应该是扩展在后面(尾部)的位置。如下:

而整数就不一样了, 4比特的定点整数,如果要把它扩展成 8 比特的长度,由于小数点我们是默认隐含在最后一个数值位的后方,因此我们扩展的这些新的比特位应该是在符号位和原来的这几个数值位中间。如下:

所以这是定点小数和定点整数需要注意的不太一样的地方。
五、案例
最后我们再来看几个加法减法的例子。
(1)案例一
这个例子是我们之前的小结当中讲过的整数补码的加法运算。 A 是正19, B 是负19, A 加 B 等于0。
接下我们让寄存器里的值保持不变,然后按照定点小数补码的方式来解读这一串二进制。
来看一下定点小数它的真值是多少。
首先它是补码的形式,定点小数补码的形式,我们要确定它的真值就得先从补码转换成原码。
A这个数它的符号位是0,表示它是一个正数,正数的补码和原码是一样的,所以上面数它的原码应该是 0. 0010011。

那么这个小数的真值是多少,我们当然也可以自己手算,但是手算我感觉还挺麻烦的,大家可以去搜索在线进制转换网站,可以去这个网站输入二进制的 0. 0010011,转换成对应的十进制。
接下来看B这个补码它的真值是多少。
首先符号位是1,表示它是一个负数。
负数的补码转换成原码应该是怎么转?从右往左找到第一个1,这个 1 前边的所有的数值位都按位取反就是001001。

右边 1 保持不变,符号位也保持不变。
所以B这个数的补码它所对应的原码应该是等于10010011。

最前边 1 表示的是负,所以下面数它的真值是 -0. 0010011,绝对值和上面一样。
所以下面补码它所对应的真值是-0.1484375 。
接下来我们按位相加得到的结果就是全为0,结合十进制来看,这个结果是正确的。
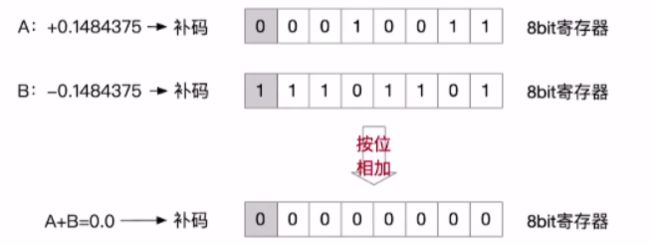
所以你会看到,前边整数补码加法的例子和小数补码加法的例子,这些寄存器里的值一模一样。
只不过前边这个例子当中,我们把这些二进制解读为定点整数的补码,而后边这个例子当中,我们把这些二进制解读为定点小数的补码。
在计算机的底层硬件看来,不管你是小数还是整数,反正你做加法,我都是用同一套逻辑来进行处理。
![]()
(2)案例二
第二个例子我们在之前也讲过的。
同样把这些二进制保持不变,按照小数定点小数补码来解读,大家可以自己试一下,反正最后的运算结果它也是正确的,大家可以尝试着把补码转变成它的真值。

(3)案例三
接下来第三个例子。
之前我们讲过整数的减法运算怎么实现的,核心就是要把减法变成等价的加法。
这是之前整数补码部分讲的一个例子,现在我们按照定点小数来进行解读,你会发现所有的这些处理,就是硬件层面的这些处理逻辑一模一样。
最后得到的结果,我们把它解释为定点小数的补码,这个结果仍然是正确的。

所以这 3 个例子,我们按照定点小数补码来解释,进行加法减法,处理的逻辑和我们之前学习的那些逻辑一模一样,因此这儿就不再赘述。
这就是定点小数的表示和运算。






