空间数据结构(四叉树/八叉树/BVH树/BSP树/k-d树)
转载说明:
原作者:KillerAery
出处:https://www.cnblogs.com/KillerAery/p/10878367.html
1 四叉树/八叉树 (Quadtree/Octree)

四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。它将已知范围的空间等分成四个相等的子空间,如此递归下去,直至树的层次达到一定深度或者满足某种要求后停止分割。
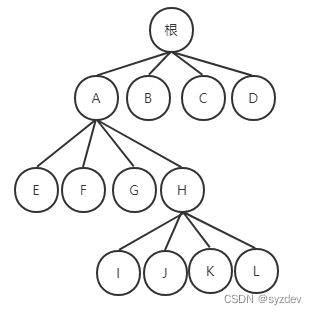
// 示例:一个四叉树节点的简单结构
struct QuadtreeNode {
Data data;
QuadtreeNode* children[2][2];
int divide; //表示这个区域的划分长度
};
// 示例:找到x,y位置对应的四叉树节点
QuadTreeNode* findNode(int x,int y,QuadtreeNode * root){
if(!root)return;
QuadtreeNode* node = root;
for(int i = 0; i < N && n; ++i){
// 通过diliver来将x,y归纳为0或1的值,从而索引到对应的子节点。
int divide = node->divide;
int divideX = x / divide;
int divideY = y / divide;
QuadtreeNode* temp = node->children[divideX][divideY];
if(!temp){break;}
node = temp;
// 如果归纳为1的值,还需要减去该划分长度,以便进一步划分
x -= (divideX == 1 ? divide : 0);
y -= (divideY == 1 ? divide : 0);
}
return node;
}
四叉树的结构在空间数据对象分布比较均匀时,具有比较高的空间数据插入和查询效率(复杂度O(logN))。

而八叉树的结构和四叉树基本类似,其拥有8个节点(三维2元素数组),其构建方法与查询方法也大同小异,不多描述。
1.1 松散四叉树/八叉树:减少边界问题
四叉树/八叉树的一个问题是,物体有可能在边界处来回,从而导致物体总是在切换节点,从而不得不更新四叉树/八叉树。而松散四叉树/八叉树正是解决这种边界问题的一种方式:首先它定义一个节点有入口边界(inner boundary),出口边界(outerboundary)。那么如何判定一个物体现在在哪个节点呢?
- 若物体还没添加进四叉树/八叉树,则检测现在位于哪个节点的入口边界内;
- 若物体先前已经存在于某个节点,则先检测现在是否越出该节点的出口边界,若越出再检测位于哪个节点的入口边界内。
在非松散的四叉树/八叉树中,入口边界和出口边界是一样的。而松散四叉树/八叉树的松散,是指出口边界比入口边界要稍微宽些(各节点的出口边界也会发生部分重叠,松散比较符合这种描述),从而使节点不容易越过出口边界,减少了物体切换节点的次数。

随之而来一个问题就是,如何定义出口边界的长度。因为太短会退化成正常四叉树/八叉树,太长又可能会导致节点存储冗余的物体。而在一篇关于松散四叉树/八叉树的论文里,实验表明出口边界长度为入口边界2倍时可以表现得很好。
1.2 四叉树/八叉树的应用
相比网格,四叉树/八叉树主要是多了层次,它们可以进行区域较大的划分,然后可以对各种检测算法进行分区域的剪枝/过滤。下面提几个应用(实际应用面很广):
- 场景管理:特别适合大规模的广阔室外场景管理。一般来说如果游戏场景是基于地形的(甚至没有高度)(如城市、平原、2D场景),那么适合用四叉树来管理。而如果游戏场景在高度轴上也有大量物体需要管理(如太空、高山),那么适合用八叉树来管理。具体例子:

- 碰撞检测:类似上面感知检测。不同划分区域保证不会碰撞的情况下,就能快速过滤与本物体不同区域的其他潜在物体碰撞。
- 光线追踪(Ray Tracing)过滤:光线追踪渲染,可使用八叉树来划分3D空间区域,从而过滤掉大量不必要的区域。
1.3 参考
【1】《游戏编程精粹2(Game Programming Gems 2)》 Mark A. Deloura [2003-12]
【2】松散八叉树 | CLOUDGRASSLAND
【3】一篇论文:Loose octree: a data structure for the simulation of polydisperse particle packings
2 层次包围盒树 (Bounding Volume Hierarchy Based On Tree)
层次包围盒树(BVH树)是一棵多叉树,用来存储包围盒形状。它的根节点代表一个最大的包围盒,其多个子节点则代表多个子包围盒。此外为了统一化层次包围盒树的形状,它只能存储同一种包围盒形状(计算机的包围盒形状有球体/AABB/OBB/k-DOP,若不清楚这些形状术语可以自行搜索了解)。常用的层次包围盒树有AABB层次包围盒树和球体树。
2.1 AABB包围盒树
下图为层次AABB包围盒树。把不同形状粗略用AABB形状围起来看作一个AABB形状(为了统一化形状),然后才建立层次AABB包围盒树。
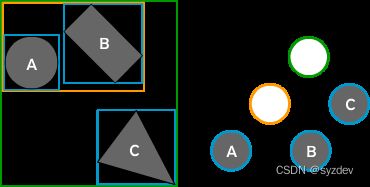
在物理引擎里,由于物理模拟,大部分形状都是会动态更新的,例如位移/旋转都会改变形状。于是就又有一种支持动态更新的层次包围盒树,称之为动态层次包围盒树。它的算法核心大概:形状的位移/旋转/伸缩更新对应的叶节点,然后一级一级更新上面的节点,使它们的包围体包住子节点。
2.2 球体包围盒树
球体是最容易计算的一类包围盒,而且球体树构造速度可以很快,因此球体树可被用作粗略松散但快速的空间划分结构。快速构造松散球体树的步骤(以三角形物体为例):
- 计算出包围所有三角边顶点的最小球体包围盒,作为根节点;
- 以球心为坐标系原点,其坐标系X轴划分出在该X轴左右的三角形,并将这些分别放入左子节点、右子节点中;
- 重复步骤1、2,最后得到一棵球体树。
在步骤2中,还可以按X轴,Y轴,Z轴的顺序轮流划分,即第一次步骤2划分用X轴,第二次步骤2划分用Y轴…

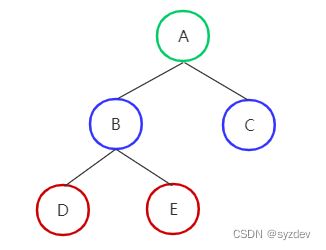
这样生成的球体树是粗糙的,但是其平衡效果并不差,且最重要的是它的构造时间复杂度只有O(NlogN)。
2.3 层次包围盒树的应用
- 碰撞检测:在Bullet、Havok等物理引擎的碰撞粗测阶段,使用一种叫做 动态层次AABB包围盒树(Dynamic Bounding Volume Hierarchy Based On AABB Tree) 的结构来存储动态的AABB形状。
然后通过该包围盒树的性质(不同父包围盒必定不会碰撞),快速过滤大量不可能发生碰撞的形状对。 - 射线检测/挑选几何体:射线检测从层次包围盒树自顶向下检测是否射线通过包围盒,若不通过则无需检测其子包围盒。这种剪裁可让每次射线检测平均只需检测O(logN)数量的形状。通过一个点位置快速挑选该点的几何体也是类似的原理。
- 视锥剔除:对BVH树进行中序遍历的视锥测试,如果一个节点所代表的包围盒不在视锥范围内,那么其所有子节点所代表的包围盒都不会在视锥范围内,则可以跳过测试其子节点。在这个遍历过程中,通过测试的节点所代表的几何体才可以发送渲染命令。
- 光线追踪(Ray Tracing)过滤:光线追踪渲染,可使用BVH来进行基于物体的划分,这样光线测试也可以过滤掉大量不必要的碰撞物体,效率一般比基于空间的划分还要好上一些。
- 辅助BSP树构建:在BSP树的构建中,利用球体树辅助,可以将复杂度从O(Nlog²N)下降为O(NlogN)的复杂度。
2.4 参考
【1】Game Physics: Broadphase – Dynamic AABB Tree | Ming-Lun “Allen” Chou | 周明倫
【2】《游戏编程精粹5(Game Programming Gems 5)》 Kim.Pallister [2007-9]
【3】Real-Time Collision Detection for Dynamic Virtual Environments
3 BSP树 (Binary Space Partitioning Tree)
BSP tree是一棵二叉树,中文译名为二维空间分割树,在游戏工业算是老功臣了,第一次被应用用是在1993年的商业游戏《DOOM》上,可是随时渲染硬件的进步,基于BSP树的渲染慢慢淘汰。但是即使在今天,BSP仍是在其他分支(引擎编辑器)不可或缺的一个重要数据结构。
BSP tree在3D空间下其每个节点表示一个平面,其代表的平面将当前空间划分为前向和背向两个子空间,分别对应左儿子和右儿子。
2D空间下,BSP树每个节点则表示一条边,也可以将2D空间划分成前后两部分。
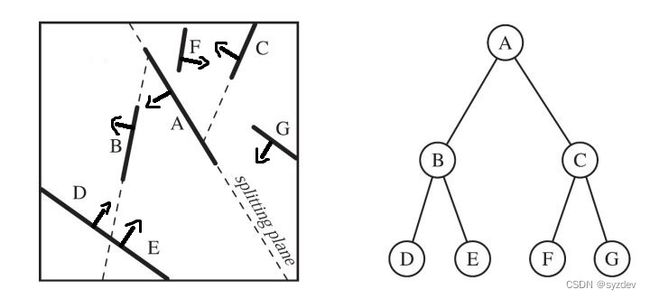
// BSP tree节点结构示例
class BSPTreeNode {
Plane plane; // 平面
BSPTreeNode* front; // 前向的节点
BSPTreeNode* back; // 后向的节点
//Data data; // 数据
};
3.1 BSP树的构建
3D空间下要构造一棵较平衡的BSP树,则需要尽可能每次划分出一个节点时,让其左子树节点数和右子树节点数相差不多:
- 在一个平面形状集合里,用其中一个平面构造一个BSP树节点时,需满足它前方的平面形状数和后方的平面形状数之差 小于 一定阈值;若超过阈值则尝试用下一个形状来构造。一个麻烦的问题是当2个平面形状是相交时,即出现平面形状既可以在前方也可以在后方的情况。这时候就需要一个将该形状切割成两个子形状,从而可以一个添加在前方,一个添加在后方,避免冲突。
- 构造完一个节点则移除对应的平面,该节点前面的平面形状和后面的平面形状则作为两个子平面形状集合。
- 对这两个子集合以重复步骤1、2继续构造出两个子节点,并作为本节点的左右儿子。
- 最后所有平面形状都被用于构造节点,组成了一棵BSP树。
由于需要进行N次划分,每次划分后,要在子集合里一个个挑选合适的平面(需要logN次遍历),为了评定合适又需要与子集合里所有其它形状比较前后位置(需要logN次比较),因此可以知道BSP树构造的平均时间复杂度为 O(Nlog²N)
判断点在平面前后算法:平面的法向量为(A,B,C),则平面方程为:Ax+By+Cz+D=0
将点(x0,y0,z0)代入方程,得distance=Ax0+By0+Cz0+D
若distance<0,则在平面背后;
若distance=0,则在平面中;
若distance>0,则在平面前方。
3.2 加速构建BSP树的球体树方法
由于BSP树构造的平均时间复杂度为O(Nlog²N),因此其往往更适合针对静态物体进行离线构造(预处理)。但在每次对关卡进行细微的改动时,设计师可能需要等待几分钟,这时间虽然不影响程序运行效率,但拖延了开发效率。一个比较好的办法就是快速构造一棵粗略的球体树,借此结构更快的构造BSP树。
- 我们可以先对所有平面形状构造一棵球体树,同时需要每个节点额外记录所拥有的形状(它和它所有子包围盒所代表的形状)数量,整个过程时间复杂度为O(NlogN)。(如何快速构造球体树,在BVH的球体树部分已经说明)
- 然后我们按照正常构造BSP树的方法,每次划分选择一个平面形状,但是判定它前方形状数和后方形状数时不判断一个个形状在平面前后,而是判断球体包围盒在平面前后。
- 只要一个球体包围盒完全在该平面前面或后面,那么它和它所有子包围盒代表的形状必定在平面前面或后面;若球体包围盒与平面相交,则需要分解成它所有子球体包围盒,再将这些球体包围盒与平面比较前后。
- 由于球体包围盒节点记录了形状数量,所以容易判断球体和平面前后关系后,得到选择某个平面时前后的形状数。
- 最后我们构造出了一棵BSP树。
此方法虽然生成的是一棵粗略、可能不是最平衡的BSP树,但是只需要O(nlogn)的时间复杂度,每次对关卡做出改动时,其用时可能只有几秒,这对设计者来说是相当理想的等待时间了。
3.3 BSP树的应用
- 自动生成室内portal
大型室内场景游戏引擎基本离不开portal系统:
- portal系统可在运行时进行额外的视野剔除,过滤掉很多被遮挡的物体渲染,有效地优化室内渲染。
- portal系统还可以离线构造PVS(潜在可见集),计算出在某个划分区域潜在可以看到哪些其他区域,将这些数据存储成一个潜在可见集;在运行时根据该集合实时加载潜在可看到的区域。
但是对于关卡编辑师来说,对每个房间/大厅/走廊/门…手动放置每个portal无疑是极大的工作量。于是有一种利用BSP树自动生成portal的做法,大致做法是:
- 首先,将室内需要渲染的墙体/门/柱子等室内较大物体所代表的边缘作为需要处理的平面,然后基于这些平面构造BSP树。将BSP树节点相连着的左节点视为一个儿子,右节点视为一个邻居。
- 将BSP树节点相连着的左节点视为一个儿子,右节点视为一个邻居。
- 所有相连的父子节点所代表的平面组成了一个凸多边形房间。
- 计算每个相邻的房间之间相衔接的点,称为portal点。
建议结合看图理解,一个示例:
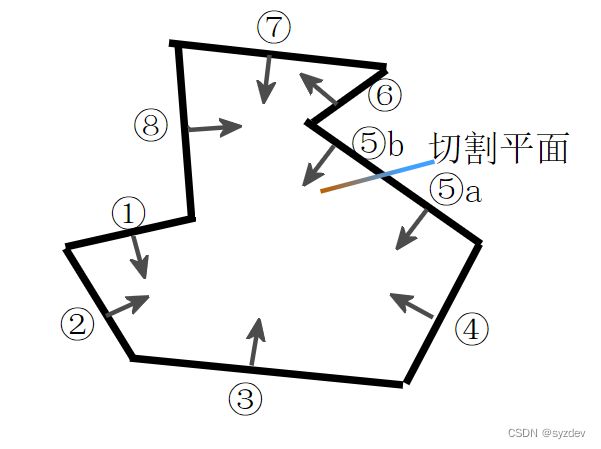
根据定义,在BSP树找到了3个凸多边形房间。

在各个相邻房间之间创建好portal点对(2个绿点,绿线表示portal平面):

基于portal系统运算得到的视野(进行了2次额外的视野剔除):

portal系统实际上是非常复杂的,但非常有价值(良好优化的室内FPS游戏基本不会缺少它)。由于其适合离线构造的特性,这种系统往往是编辑器程序员所需要使用,这里仅仅只能点下自动生成portal的皮毛,更具体的细节可看本节参考。
- 自动生成导航网格:导航网格(Nav Mesh)是一种表示凸多边形的节点,目前主流游戏的游戏AI寻路中最常用的节点种类。通过用导航网格,A*寻路所要搜索的节点数量大大减少且变得灵活。因此我们可以预先计算可移动地形和静态障碍,得到一个不规则的大地图形状(可能有凹处也可能有中空处),然后以该形状的所有边来构造一棵BSP树来分割得到若干个凸多边形房间,而这些分割出来的每个凸多边形都是一个导航网格。
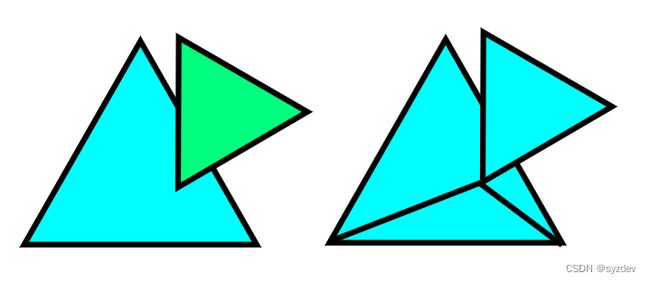
- 构造CSG(Constructive Soild Geometry)几何体:几何体编辑是一个常见的编辑器功能,设计者往往需要通过基本图形(立方体、球体、圆柱体、圆锥等)来进行并集、交集或差集,从而得到一个复合的几何体,也就是所谓的CSG几何体。而BSP树可以很好的处理和表示这些CSG几何体,UE4引擎中的几何体编辑就是采用BSP方式。例如两个三角形(图左)可以通过BSP方式并集成为CSG几何体(图右)。
- 渲染顺序优化(不实用、已淘汰过时):首先根据摄像机的位置,遍历BSP树找到并记录其位置相对应的叶节点,称之eyeNode,它将会是顺序遍历渲染的一个重要的中止条件。
由于eyeNode往往是在一些平面的前面,另一些平面的后面,所以为了达到正确的从近到远的顺序,需要两次不同方向的遍历。
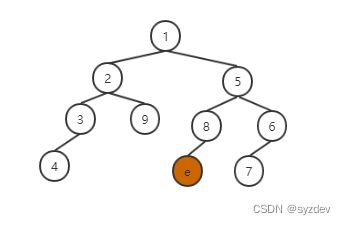
在至少二十多年前,老旧硬件是没有深度缓存,程序员使用BSP树从远到近渲染(从远处到摄像机位置)三角形图元,避免较远的三角形覆盖到较近的三角形上,从而到达正确的三角形图元渲染顺序,这也就是古老的画家算法。
从远处到eyeNode处的遍历顺序:
第一次遍历,左中右顺序,从根节点开始,直到eyeNode停止;
第二次遍历,右中左顺序,从根节点开始,直到eyeNode停止。
该BSP树节点代表的数据应该是一个三角形(渲染的基本图元),因为恰好三角形也是个平面形状,因此该BSP树节点代表的平面也就是其数据本身。
而今天对于现代渲染硬件来说,虽然对BSP树近到远渲染(从摄像机位置到远处)物体可以减少overdraw(即对像素的重复覆写)开销,但是并不实用,花费昂贵的CPU代价换来少量GPU优化。
3.4 参考
【1】BSPTreesGameEngines-1
【2】BSPTreesGameEngines-2
【3】Quake3BSPRendering
【4】Real-Time Rendering SPEEDING UP RENDERING Lecture 04 Marina Gavrilova. - ppt download
【5】BSP技术详解1 - Dreams - 博客园
【6】BSP技术详解2 - Dreams - 博客园
【7】BSP技术详解3 - Dreams - 博客园
【8】BSP技术详解(补充)–pvs算法 - Dreams - 博客园
【9】场景管理–BSP - bitbit - 博客园
【10】《游戏编程精粹5(Game Programming Gems 5)》Kim.Pallister [2007-9]
【11】《游戏编程精粹6(Game Programming Gems 6)》Michael Dickheiser [2007-11]
4 k-d树 (k-dimensional tree)
k-d树是一棵二叉树,其每个节点都代表一个 k维坐标点:
- 树的每层都是对应一个划分维度(取决于你定义第i层是哪个维度)
- 树的每个节点代表一个超平面,该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分,一部分在其左子树,另一部分在其右子树
实际上,k-d树就是一种特殊形式的BSP树(轴对齐的BSP树)。
// 一种实现方式示例:二维k-d树节点
class KdTreeNode{
Vector2 position; // 位置
int dimension; // 当前所属层的维度
KdTreeNode* children[2]; // 两个子树
//Data data; // 数据
};
举例,一棵k-d树(k=2)的结构如图:

根据第一层划分维度为X,第二层为Y,第三层为X,所以该k-d树(k=2)对应代表划分的空间,看起来应该是这样的:

4.1 k-d树的应用
- 划分区域(不实用):虽然k-d树也可以划分区域,但是k-d树的构建往往非常耗时,且不支持动态构建(即发生变化需要重新构建),因此目前游戏开发还是比较少用得上。
- 最近邻静态目标查找(很少用,了解即可):通过最近邻查找算法,可以剪枝了大量无需遍历的子树,效率提升得很好,其平均时间复杂度可以达到O(n^(1−1/k)),k为维度。
4.2 参考
【1】k-d tree算法原理及实现 – 磊磊落落的博客
5 自定义区域
一个自定义区域一般是一个凸多边形,然后可通过一些编辑器手动设置好其各顶点位置,最终手工划分出一块凸多边形区域。3D凸多面体一般很少用,即使在要求划分区域属于同一XOZ面不同高度的3D世界里,考虑到性能,可能更适合用凸多边形+高度来划分区域。
此外一提,能不用凹多边形就不用。因为许多程序算法都可以应用在凸多边形上,而相对应用于凹多边形上可能行不通或者得用更低效的算法
为了达到自定义区域之间的无缝衔接,游戏程序还往往采用图(或者树)结构来存储这些自定义区域,表示它们之间的联系。
// 自定义区块示例
class Chunk{
Data data; // 区域数据
std::vector<Vector2> vertexs; // 区域凸多边形顶点
std::vector<Chunk*> neighbors; // 邻近区域
};
5.1 判断目标点是否在凸多边形区域算法
既然用到了凸多边形区域,那就顺便提一提如何判断目标点是否在凸多边形区域,而且也不是很难:

目标点p对凸多边形每个顶点之间建立一个向量vec(如:v1-p),该向量与其对应的顶点的边edge(如:v2-v1)进行叉乘,得到一个叉积值。若每个叉积值的符号都一样(都是正数/都是负数),则证明点在凸多边形内。否则,则证明点不再凸多边形内。
举个例子:
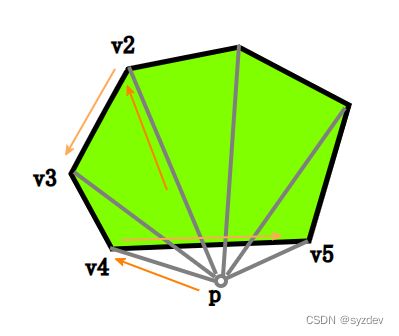
因为 sign((v4−p)×(v5−v4))≠sign((v2−p)×(v3−v2)),所以可知目标点不在凸多边形内。
bool Chunk::inChunk(Vector2 p){
int size = vertexs.size();
for(int i = 0; i < size; ++i){
// 假设凸多边形的边edge都是逆时针方向
Vector2 edge = vertex[(i+1)%size]-vertex[i];
Vector2 vec = vertex[i] - p;
int result = cross(edge,vec);
// 若点在凸多边形内,得到的叉积值应都是正数
if(sign(result) == 0)return false;
}
return true;
}
显而易见的,该算法时间复杂度为O(|V|),V为凸多边形顶点数。
5.2 自定义区域划分的应用
自定义区域是非常灵活的,往往可以应用于任何游戏,特别适合非规则世界的游戏。
- 更灵活的渲染分区块渲染:典型需要灵活划分不规则区块的游戏莫过于赛车游戏,其赛道往往崎岖蜿蜒,所以其实潜在大量区域不必渲染。但因为赛道布局的不规则,所以这些路段区域往往需要手工设置划分。
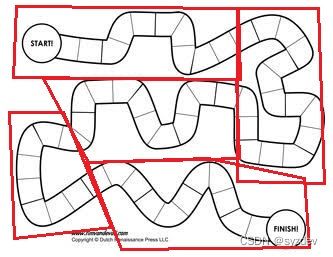
当汽车在相应的红线区域时,不必渲染其他红线区域(或使用低耗渲染),因为往往汽车的视野基本都是往前看,狭隘的视野可观察到的地方实际上很有限。当然除了赛车游戏,还有许多其他游戏都需要用到这种划分,减少不必要的渲染。 - 地图载入:如图,先将关卡地图划分成①②③④地图块。然后再自定义划分好Chunk A/B/C/D,并且设置好相应规则用于加载地图块:当玩家在Chunk A时,加载①;在Chunk B时加载①②;在Chunk C时加载②③;在Chunk D时加载③④。
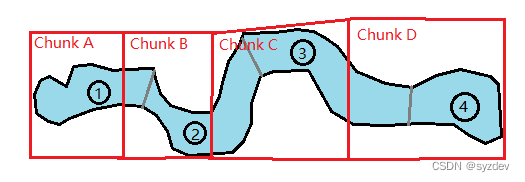
这样可以实现一些基本的地图载入衔接,在相应的Chunk能渲染远处本该看到的地图块。
6 结语
总的来说,游戏开发最常用的空间数据结构是四叉/八叉树、BVH树,而BSP树基本上只能应用于编辑器上,k-d树则几乎没有可以应用的地方。简单整理了如下表格:
| 数据结构 | 适用情形 | n的数量级 | 构造所需时间 | 是否可以动态更新 | 占用空间 |
|---|---|---|---|---|---|
| 四叉树 | 场景管理(基于地形或不含高度)、渲染 | 物体数量 | O(n*logn) | 是 | 大(取决于区域大小和物体数量) |
| 八叉树 | 场景管理、渲染 | 物体数量 | O(n*logn) | 是 | 大(取决于区域大小和物体数量) |
| BVH树 | 任何情形(包括物理、渲染) | 物体数量 | O(n*logn) | 是 | 中(取决于物体数量) |
| BSP树 | 编辑器、复杂室内场景 | 平面数量 | O(n*log²n) | 否 | 大(取决于平面数量) |
| k-d树 | - | 物体数量 | O(knlogn) | 否 | 中(取决于物体数量) |