常用的空间数据结构(网格/四叉树/八叉树/BSP树/k-d树/BVH/自定义划分)

空间划分的数据结构(网格/四叉树/八叉树/BSP树/k-d树/BVH/自定义划分)

目录

• 网格 (Grid)
  • 网格的应用
• 四叉树/八叉树 (Quadtree/Octree)
  • 四叉树/八叉树的应用
• BSP树 (Binary Space Partitioning Tree)
  • 判断点在平面前后算法
  • BSP树的应用
  • 参考
• k-d树 (k-dimensional tree)
  • k-d树的构建
  • k-d树的应用
  • 参考
• 层次包围盒树 (Bounding Volume Hierarchy Based On Tree)
  • 层次包围盒树的应用
  • 参考
• 自定义区域
  • 判断点是否在凸多边形区域算法
  • 自定义区域划分的应用

前言：
在游戏程序中，空间划分往往是非常重要的优化思想。
于是博主花了一些时间去整理了游戏程序中常用的几个空间划分数据结构，并将它们大概列举出来以供笔记。

网格 (Grid)

---

这个很容易理解，即一个多维数组。平面/基于高度的空间使用二维网格数组，而3D空间使用三维网格数组。

Data girds2d[MAX_X][MAX_Y];//2D平面划分网格，二维数组
Data girds3d[MAX_X][MAX_Y][MAX_Z];//3D空间划分网格，三维数组

网格的应用

• 基于网格划分的游戏世界

例如战棋/棋类游戏，Minecraft方块游戏等。

四叉树/八叉树 (Quadtree/Octree)

---

四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。
它将已知范围的空间等分成四个相等的子空间，如此递归下去，直至树的层次达到一定深度或者满足某种要求后停止分割。

//示例：一个四叉树节点的简单结构
struct QuadtreeNode {
  Data data;
  QuadtreeNode* children[2][2];
  int divide;  //表示这个区域的划分长度
};

//示例：找到x,y位置对应的四叉树节点
QuadTreeNode* findNode(int x,int y,QuadtreeNode * root){
  if(!root)return;

  QuadtreeNode* node = root;
  
  for(int i = 0; i < N && n; ++i){
    //通过diliver来将x,y归纳为0或1的值，从而索引到对应的子节点。
    int divide = node->divide;
    int divideX = x / divide;
    int divideY = y / divide;
    
    QuadtreeNode* temp = node->children[divideX][divideY];
    if(!temp){break;}
    node = temp;
    
    //如果归纳为1的值，还需要减去该划分长度，以便进一步划分
    x -= (divideX == 1 ? divide : 0);
    y -= (divideY == 1 ? divide : 0);
  }
  
  return node;
}

四叉树的结构在空间数据对象分布比较均匀时，具有比较高的空间数据插入和查询效率（复杂度O(logN)）。

而八叉树的结构和四叉树基本类似，其拥有8个节点(三维2元素数组)，其构建方法与查询方法也大同小异，不多描述。

四叉树/八叉树的应用

它们可以进行区域较大的划分，然后可以对各种检测算法进行分区域的剪枝/过滤。
下面提几个应用（实际应用面很广）：

• 感知检测

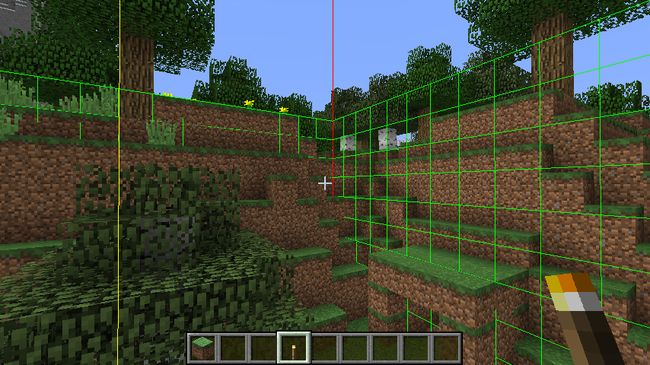
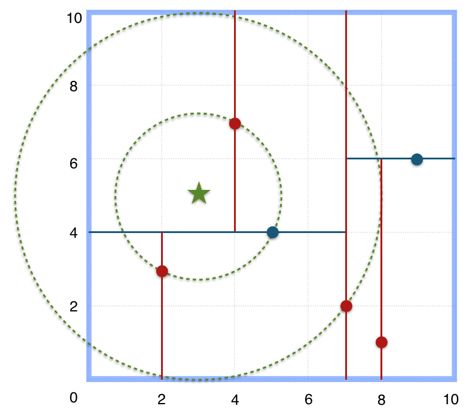
如图所示，假如保证一个（图中为绿色⚪）智能体最远不会感知到所在区域外的地方。
那么通过四叉树，可以快速过滤掉K区域外的红色目标，只需考虑K区域内的红色目标。

• 碰撞检测

类似上面感知检测。不同划分区域保证不会碰撞的情况下，就能快速过滤与本物体不同区域的其他潜在物体碰撞。

• 光线追踪（Ray Tracing）过滤

光线追踪渲染，可使用八叉树来划分3D空间区域，从而过滤掉大量不同区域。

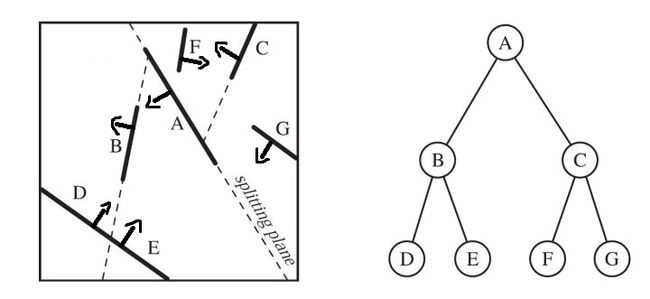
BSP树 (Binary Space Partitioning Tree)

---

BSP tree是一棵二叉树，其每个节点表示一个有向超平面形状，其代表的平面将当前空间划分为前向和背向两个子空间，分别对应左儿子和右儿子。

（为了方便说明，下文的平面一律指超平面）

如果用一种特定的方式遍历，BSP树的几何内容可以从任何角度进行前后排序。

//大致的BSP tree节点结构
class BSPTreeNode {
    std::vector vertexs;  //多边形的顶点
    Data data;                     //数据
    BSPTreeNode* front;            //前向的节点
    BSPTreeNode* back;             //后向的节点
    //...
};

要构造一棵较平衡的BSP树，其实原理很简单：尽可能每次划分出一个节点时，让其左子树节点数和右子树节点数相差不多。也就是说，用一个平面形状构造一个BSP树节点时，需满足它前方的多边形数和后方的多边形数之差 小于 一定阈值；若超过阈值则尝试用另一个形状来构造。构造完一个节点则移除对应的一个平面形状。最后所有平面形状都被用于构造节点，组成了一棵BSP树。

麻烦在于当2个平面形状是相交时，它既可以在前方也可以在后方的情况。这时候就需要一个将该形状切割成两个子形状，从而可以一个添加在前方，一个添加在后方，避免冲突。

本文就不多描述具体实现了（犯懒），感兴趣可看下面的参考列表。

结论是：BSP树构造的最坏时间复杂度为O(N²logN),平均时间复杂度为O(N²)。

判断点在平面前后算法

平面的法向量为(A,B,C)(A,B,C)，则平面方程为：
Ax+By+Cz+D=0Ax+By+Cz+D=0

将点(x0,y0,z0)(x0,y0,z0)代入方程，得
distance=Ax0+By0+Cz0+Ddistance=Ax0+By0+Cz0+D

若distance<0distance<0，则在平面背后；
若distance=0distance=0，则在平面中；
若distance>0distance>0，则在平面前方。

BSP树的应用

由于BSP树构造的平均时间复杂度为O(N²)，因此其往往更适合针对静态物体进行离线构造。

• 自动生成室内portal

大型室内场景游戏引擎基本离不开portal系统：

1. portal系统可在运行时进行额外的视野剔除，过滤掉很多被遮挡的物体渲染，有效地优化室内渲染。
2. portal系统还可以离线构造PVS(潜在可见集)，计算出在某个划分区域潜在可以看到哪些其他区域，将这些数据存储成一个潜在可见集；在运行时根据该集合实时加载潜在可看到的区域。

但是对于关卡编辑师来说，对每个房间/大厅/走廊/门...手动放置每个portal无疑是极大的工作量。于是有一种利用BSP树自动生成portal的做法，大致做法是：

1. 首先BSP树节点数据应该为需要渲染的墙体/门/柱子等室内较大物体。
2. 将BSP树节点连着的左节点视为一个儿子，右节点视为一个邻居。
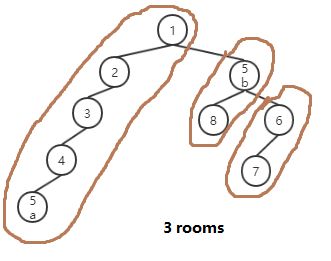
3. 所有相连的父子节点所代表的平面组成了一个凸多边形房间。
4. 计算每个相邻的房间之间相衔接的点，称为portal点。

建议结合看图理解，一个示例：

根据定义，在BSP树找到了3个凸多边形房间。

在各个相邻房间之间创建好portal点对（2个绿点，绿线表示portal平面）：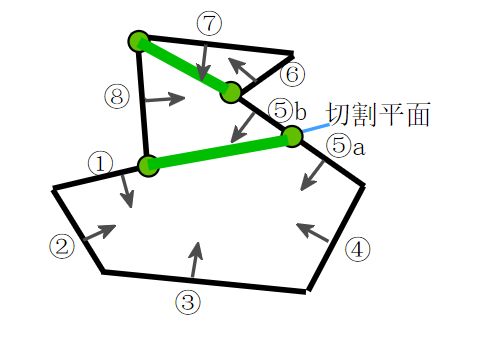

基于portal系统运算得到的视野（进行了2次额外的视野剔除）：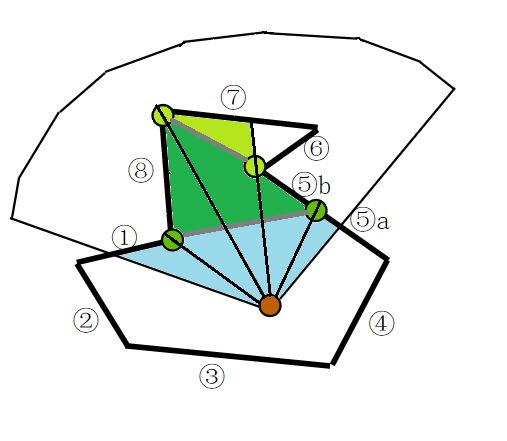

portal系统实际上是非常复杂的，但非常有价值（良好优化的室内FPS游戏基本不会缺少它）。由于其适合离线构造的特性，这种系统往往是编辑器程序员所需要使用，这里仅仅只能点下自动生成portal的皮毛，更具体的细节可看本节参考。

• 渲染顺序优化

首先根据摄像机的位置，遍历BSP树找到并记录其位置相对应的叶节点,称之eyeNode，它将会是顺序遍历渲染的一个重要的中止条件。
由于eyeNode往往是在一些平面的前面，另一些平面的后面，所以为了达到正确的从近到远的顺序，需要两次不同方向的遍历。

对于没有深度缓存的老旧硬件，对BSP树从远到近渲染（从远处往摄像机位置）三角形图元，避免较远的三角形覆盖到较近的三角形上，从而到达正确的三角形图元渲染顺序，这也就是古老的画家算法。

注：这里的节点数据应该代表为需要渲染的三角形图元。
其顺序：
第一次遍历，左中右顺序，从根节点开始，直到eyeNode停止；
第二次遍历，右中左顺序，从根节点开始，直到eyeNode停止；

对于现代渲染硬件来说，对BSP树近到远渲染（从摄像机位置往远处）物体，可以减少一些overdraw（即对像素的重复覆写）开销。

注：这里的节点数据应该代表为需要渲染的固定物体（诸如块岩石/柱子/固定的桌子椅子，这些物体往往可以用一些粗略平面代表之）。
其顺序：
第一次遍历，左中右遍历，从eyeNode开始，直到递归全部结束；
第二次遍历，右中左遍历，从eyeNode开始，直到递归全部结束；

参考

• BSPTreesGameEngines-1
• BSPTreesGameEngines-2
• Quake3BSPRendering
• Real-Time Rendering SPEEDING UP RENDERING Lecture 04 Marina Gavrilova. - ppt download
• BSP技术详解1 - Dreams - 博客园
• BSP技术详解2 - Dreams - 博客园
• BSP技术详解3 - Dreams - 博客园
• BSP技术详解(补充）--pvs算法 - Dreams - 博客园
• 场景管理--BSP - bitbit - 博客园

k-d树 (k-dimensional tree)

---

k-d树 是一棵二叉树，其每个节点都代表一个k维坐标点;
树的每层都是对应一个划分维度（取决于你定义第i层是哪个维度）;
树的每个节点代表一个超平面，该超平面垂直于当前划分维度的坐标轴，并在该维度上将空间划分为两部分，一部分在其左子树，另一部分在其右子树;

即若当前节点的划分维度为i，其左子树上所有点在i维的值均小于当前值，右子树上所有点在i维的值均大于等于当前值，本定义对其任意子节点均成立。

实际上k-d树就是一种特殊形式的BSP树（轴对齐的BSP树）。

//一种实现方式示例：二维k-d树节点
class KdTreeNode{
  Vector2 position;         //位置
  Data data;                //点数据
  int dimension;            //当前所属层的维度
  KdTreeNode* children[2];  //两个子树
};

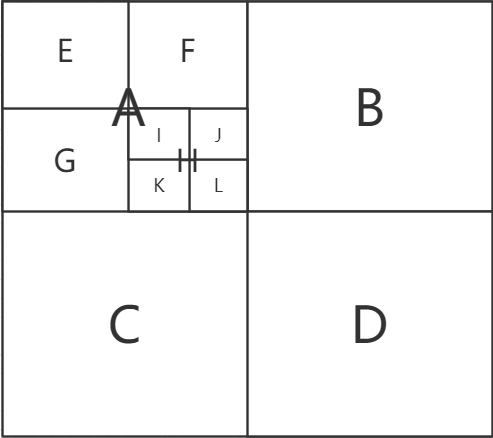
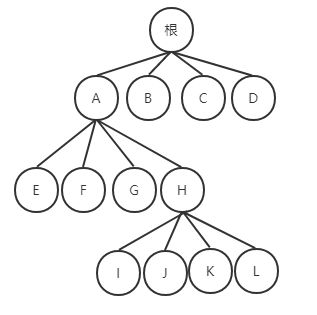
举例，一棵k-d树（k=2）的结构如图：

根据第一层划分维度为X，第二层为Y，第三层为X，
所以该k-d树（k=2）对应代表划分的空间，看起来应该是这样的：

k-d树的构建

基本定义有了，接下来问题就是如何构建k-d树。

此外一提，一棵平衡的k-d tree对最近邻搜索、空间搜索等应用场景并非是最优的。

常规的k-d tree的构建过程为：
一、循环依序取数据点的各维度来作为划分维度。
二、取数据点在该维度的中值作为切分超平面，将中值左侧的数据点挂在其左子树，将中值右侧的数据点挂在其右子树。
三、递归处理其子树，直至所有数据点挂载完毕。

//一种构建方法示例,此处伪代码省略了Data部分
KdTreeNode* createKdTree(int dimension, std::vector& points, int beginIndex, int endIndex) {
    if(beginIndex >= endIndex) return nullptr;
  
    //先根据当前划分维度来排序[beginIndex,endIndex)区域的点
    if (dimension == 0) {
      std::sort(points.begin() + beginIndex, points.begin() + endIndex, 
      [](Vector2 & a, Vector2 & b) {return a.x < b.x; });
    }
    else if (dimension == 1) {
      std::sort(points.begin() + beginIndex, points.begin() + endIndex,
      [](Vector2 & a, Vector2 & b) {return a.y < b.y; });
    }
    //中值选择
    int midValueIndex = points.size() / 2;
    //以该中值创建一个划分节点
    KdTreeNode* node = new KdTreeNode(points[midValueIndex]);

    //递归构建子树
    //左子树为较小值，区间应该为[beginIndex,midValueIndex)
    node->children[0] = createKdTree(!dimension, points, beginIndex, midValueIndex);
    //左子树为较大值，区间应该为[midValueIndex+1,endIndex)
    node->children[1] = createKdTree(!dimension, points, midValueIndex + 1, endIndex);

    return node;
}

构建k-d树的两种优化角度:

• 切分维度选择优化
  构建开始前，对比数据点在各维度的分布情况，数据点在某一维度坐标值的方差越大分布越分散，方差越小分布越集中。从方差大的维度开始切分可以取得很好的切分效果及平衡性。
• 中值选择优化
  第一种，算法开始前，对原始数据点在所有维度进行一次排序，存储下来，然后在后续的中值选择中，无须每次都对其子集进行排序，提升了性能。
  第二种，从原始数据点中随机选择固定数目的点，然后对其进行排序，每次从这些样本点中取中值，来作为分割超平面。该方式在实践中被证明可以取得很好性能及很好的平衡性。

k-d树的应用

• 最近邻静态目标查找

在编写游戏AI时，一个智能体查找一个最近静态目标（例如最近的房子/固定NPC/固定资源）是容易的，对所有单位一个个遍历检测最短平方距离即可（时间复杂度O(N)）。当数百个单位（集群AI）都需要寻找最近的静态目标时，这时候可能比较适合使用基于k-d树的最近邻查找算法：

一、首先记录一个输入点与节点的最短距离平方minDisSq，初始值为无穷大。

二、利用k-d树，对其进行深度优先遍历，每次遍历节点的步骤：

1. 先计算输入点在第i维度值与当前节点的第i维度值之差的平方值sq1，并与minDisSq比较大小。
2. 如果(sq1≥minDisSq)(sq1≥minDisSq)，则证明当前节点划分的另一边区域（其中一个子树）不可能有更近的点，所以可剪枝该区域，即只遍历当前节点划分的同区域（遍历另一个子树）。
3. 如果(sq1

三、最后得到一个minDisSq对应的节点。

//一个最近邻目标查找代码示例

//此处为了方便代码编写，使用2个全局变量记录
float minDisSq = FLT_MAX;
KdTreeNode* gResult = nullptr;

//递归函数，调用该函数后，更新后的gResult即是结果。
void findNearest(Vector2 point, KdTreeNode* node) {
    if(!node) return;

    float sq1;
    //计算输入点在第i维度值与当前节点的第i维度值之差的平方值sq1
    if (node->dimension == 0) {
      sq1 = (point.x - node->position.x)*(point.x - node->position.x);
    }
    else if (node->dimension == 1) {
      sq1 = (point.y - node->position.y)*(point.y - node->position.y);
    }
    
    //大于等于minDisSq，证明当前节点划分的另一边区域（其中一个子树）不可能有更近的点
    if (sq1 >= minDisSq) {
        //遍历1个子树（同区域的）。
        findNearest(point,node->getSameDivideArea(point));
    }
    //小于minDisSq，证明当前节点划分的两个区域（两个子树）都可能有更近的点
    else {
        //计算输入点和当前节点的距离平方值sq2
        float sq2  = (point.x - node->position.x)*(point.x - node->position.x)
                    +(point.y - node->position.y)*(point.y - node->position.y);
        //再与minDisSq比较，若更短则更新minDisSq,并记录该点
        if (sq2 < minDisSq) {
            minDisSq = sq2;
            gResult = node;     
        }
    
        //遍历2个子树，先遍历同区域，后遍历另一区域
        findNearest(point, node->getSameDivideArea(point));
        findNearest(point, node->getDifferntDivideArea(point));
    }
}

如下图例子，我们想找到与点(3,5)最近的目标:

通过算法，我们从绿色箭头顺序遍历，
并剪枝了一些不可能的子树，灰色部分即是剪枝部分: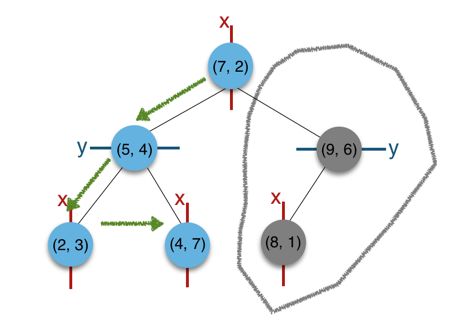

k-d树剪枝了大量在较远区域的目标，效率提升地很好，其平均时间复杂度可以达到O(n1−1k)O(n1−1k)，k为维度。

至于为什么目标最好是静态的，因为kd树的构建往往非常耗时，如果动态则需要时时重新构建，所以更适合预先构建静态目标的kd树。

注：还有一种称之为主席树的动态更新方法，具体效率如何博主则没过多深入研究。

参考

• k-d tree算法原理及实现 – 磊磊落落的博客

层次包围盒树 (Bounding Volume Hierarchy Based On Tree)

---

层次包围盒简称BVH；而层次包围盒树是一棵二叉树，用来存储包围盒形状。
它的根节点代表一个最大的包围盒，往下2个子节点则代表2个子包围盒。

此外为了统一化层次包围盒树的形状，它只能存储同一种包围盒形状。

计算机常用的包围盒形状有球/AABB/OBB/k-DOP，若不清楚这些概念可以自行搜索了解。

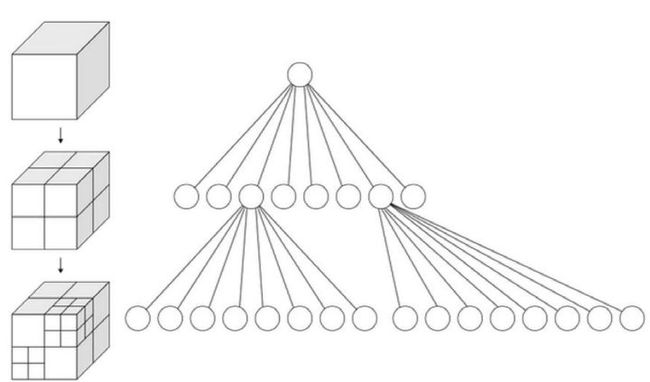
下图为层次AABB包围盒树。把不同形状粗略用AABB形状围起来看作一个AABB形状（为了统一化形状），然后才建立层次AABB包围盒树。

常见的层次包围盒树有层次AABB包围盒树，层次球包围盒树。

在物理引擎里，由于物理模拟，大部分形状都是会动态更新的，例如位移/旋转/伸缩都会改变形状。于是就又有一种支持动态更新的层次包围盒树，称之为动态层次包围盒树。它的算法核心大概：形状的位移/旋转/伸缩更新对应的叶节点，然后一级一级更新上面的节点，使它们的包围体包住子节点。

一般来说这个结构常用于物理引擎，应用面较窄，本文就不多做讲解。

层次包围盒树的应用

• 碰撞检测

在Bullet、Havok等物理引擎的碰撞粗测阶段，往往使用一种叫做 动态层次AABB包围盒树(Dynamic Bounding Volume Hierarchy Based On AABB Tree) 的结构来存储动态的AABB形状。
然后通过该包围盒树的性质（不同父包围盒必定不会碰撞），快速过滤大量不可能发生碰撞的形状对。

• 射线检测

射线检测从层次包围盒树自顶向下检测是否射线通过包围盒，若不通过则无需检测其子包围盒。
这种剪裁可让每次射线检测平均只需检测O(logN)数量的形状。

参考

• Game Physics: Broadphase – Dynamic AABB Tree | Ming-Lun "Allen" Chou | 周明倫
• (还有一些论文，有空再贴出)

自定义区域

---

一个自定义区域一般是一个凸多边形，然后可通过一些编辑器手动设置好其各顶点位置，最终手工划分出一块凸多边形区域。3D凸多面体一般很少用，即使在要求划分区域属于同一XOZ面不同高度的3D世界里，考虑到性能，可能更适合用凸多边形+高度来划分区域。

相信我，能不用凹多边形就不用，因为许多程序算法都可以应用在凸多边形上，而相对应用于凹多边形上可能行不通或者得用更低效的算法。

为了达到自定义区域之间的无缝衔接，游戏程序还往往采用图（或者树）结构来存储这些自定义区域，表示它们之间的联系。

//区域
class Chunk{
  Data data;                      //区域数据
  std::vector vertexs;   //区域凸多边形顶点
  std::vector neighbors;  //邻近区域
};

判断点是否在凸多边形区域算法

既然用到了凸多边形区域，那就顺便提一提如何判断点是否在凸多边形区域，而且也不是很难：

点对凸多边形每个顶点之间建立一个线段2D向量，该向量与其对应的顶点的边进行叉乘，得到一个叉积值。
若每个叉积值的符号都一样（都是正数/都是负数），则证明点在凸多边形内。
否则，则证明点不再凸多边形内。

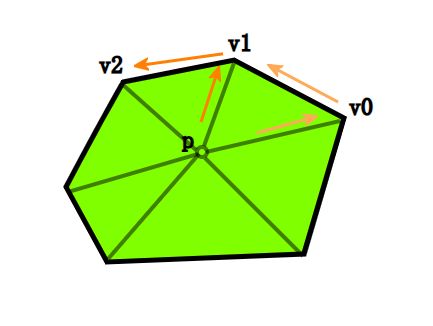
再举个例子：

如图，可以看到
sign((v4−p)×(v5−v4))≠sign((v2−p)×(v3−v2))sign((v4−p)×(v5−v4))≠sign((v2−p)×(v3−v2))

因此可知点不在凸多边形内。

bool Chunk::inChunk(Vector2 p){
  int size = vertexs.size();
  for(int i = 0; i< size; ++i){
    Vector2 edge = vertex[(i+1)%size]-vertex[i];
    Vector2 vec = vertex[i] - p;
    //边都是逆时针方向，线段向量方向为指向凸多边形的顶点。
    //若点在凸多边形内，得到的叉积值应都为正数
    int result = cross(edge,vec);
    
    if(sign(result) == 0)return false;
  }
  return true;
}

显而易见的，该算法时间复杂度为O(|V|)；V为凸多边形顶点数。

若让该算法进一步提升效率，可让算法达到O(log|V|)的效率，大概思想是用叉积判断点在边的左右加二分查找。

不过考虑到凸多边形顶点数量一般不会很多（除非开发者丧心病狂的使用几十边形乃至上百千，这已经是基本不可能的事了），就提一提吧。

自定义区域划分的应用

自定义区域是非常灵活的，往往可以应用于任何游戏，特别适合非规则世界的游戏。

• 更灵活的渲染分区块渲染

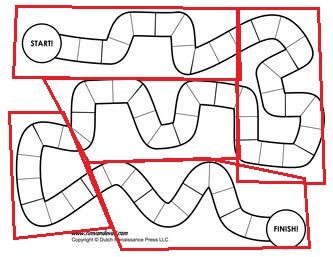
典型需要灵活划分不规则区块的游戏莫过于赛车游戏，其赛道往往崎岖蜿蜒，所以其实潜在大量区域不必渲染。但因为赛道布局的不规则，所以这些路段区域往往需要手工设置划分。

当汽车在相应的红线区域时，不必渲染其他红线区域（或使用低耗渲染），因为往往汽车的视野基本都是往前看，狭隘的视野可观察到的地方实际上很有限。

当然除了赛车游戏，还有许多其他游戏都需要用到这种划分，减少不必要的渲染。

• 地图载入

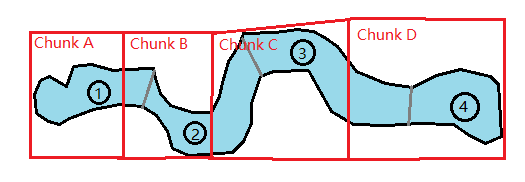
如图，先将关卡地图划分成①②③④地图块。
然后再自定义划分好Chunk A/B/C/D，并且设置好相应规则用于加载地图块：当玩家在Chunk A时，加载①；在Chunk B时加载①②；在Chunk C时加载②③；在Chunk D时加载③④。

这样可以实现一些基本的地图载入衔接，在相应的Chunk能渲染远处本该看到的地图块。