- 快速排序Java代码简洁实现
SKY技术修炼指南
算法
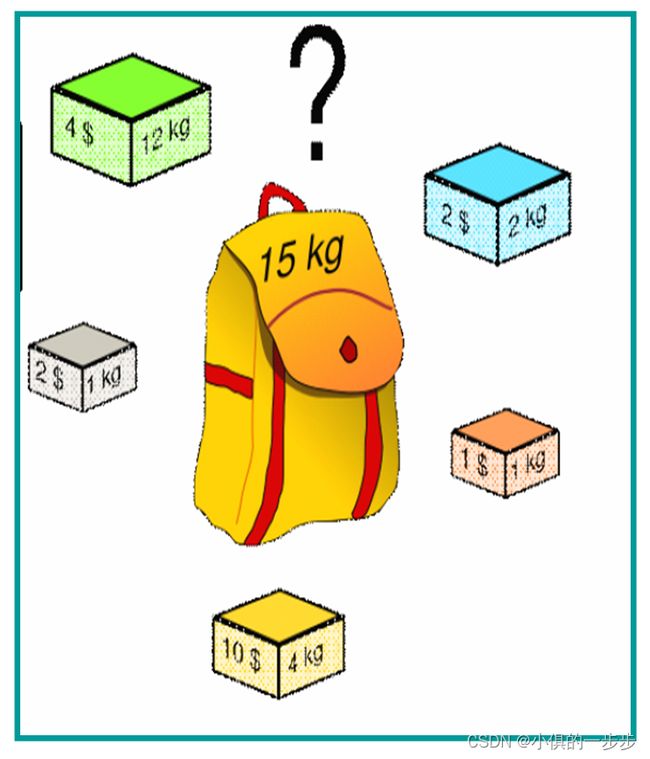
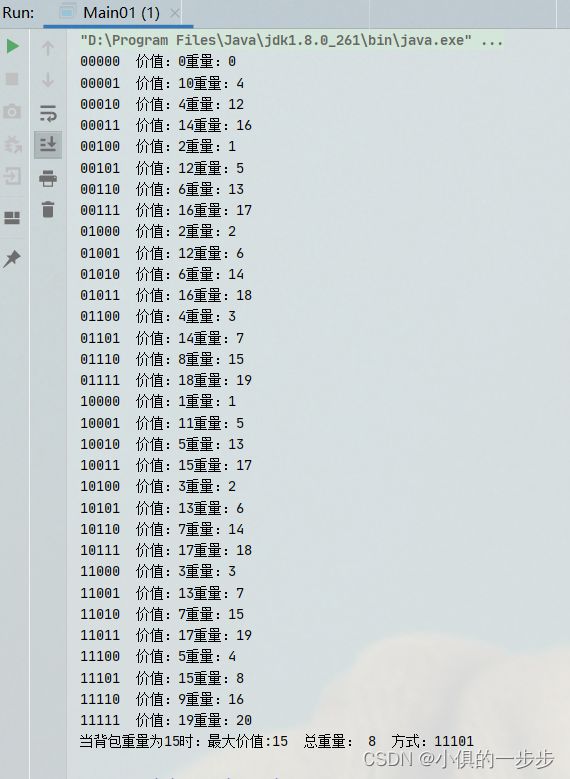
学习过数据结构的同学们都知道,快速排序算法是一种时间复杂度为O(nlogn)的排序算法,在各种排序算法中算是较为高效的方法,企业面试中也经常有手撕快排的环节。本文将阐述算法的基本思想,并用Java代码的形式实现快速排序代码。算法思想快速排序主要采用分治的基本思想,每次将一个位置上的数据归位,此时该数左边的所有数据都比该数小,右边所有的数据都比该数大,然后递归将已归位的数据左右两边再次进行快排,从而
- Android Gson复杂数据结构(如Map、List)的序列化逻辑原理剖析
一、复杂数据结构序列化概述1.1复杂数据结构处理的重要性在Android开发中,JSON数据往往包含复杂数据结构,如Map、List等。Gson作为常用的JSON处理库,其对复杂数据结构的序列化能力至关重要。准确处理这些结构能确保数据在网络传输、本地存储等场景下保持完整的语义和结构,避免数据丢失或格式错乱。1.2核心处理流程Gson对复杂数据结构的序列化主要包含以下步骤:类型识别:确定待序列化对象
- 如何防止重复提交订单?
天天摸鱼的java工程师
java
如何防止重复提交订单?作者:Java后端开发工程师一、背景介绍:为什么会产生重复提交?在电商平台中,用户提交订单是一个非常敏感的动作。这通常涉及:库存扣减优惠券核销支付下单消息发送但用户总喜欢:点两次“提交订单”按钮网络卡顿时刷新页面使用浏览器回退再次提交结果就是:重复提交订单,造成资源浪费,甚至业务损失!二、问题分析:重复提交的常见场景场景示例用户行为多次点击按钮、浏览器刷新接口幂等性差接口无幂
- 如何设计一个高并发短链接服务(如 bit.ly)?
天天摸鱼的java工程师
java
如何设计一个高并发短链接服务(如bit.ly)?引言:在社交媒体营销、短信推广等场景中,短链接服务已成为互联网基础设施的关键组件。全球每天有数十亿短链接被创建,如Bitly、TinyURL等服务每天处理数十亿请求。作为一名拥有8年经验的Java架构师,我曾主导设计过日处理千万级短链接的系统。今天我将从原理到实现,深度解析如何构建一个高性能、高可用、可扩展的短链接服务。一、业务场景与技术挑战1.1核
- 如何将电商单体应用拆分为微服务?拆分粒度如何权衡?
天天摸鱼的java工程师
微服务java
如何将电商单体应用拆分为微服务?拆分粒度如何权衡?引言:在电商行业高速发展的今天,系统扩展性和交付速度成为核心竞争力。许多企业初期采用单体架构快速上线,但随着业务规模扩大,单体应用逐渐成为制约发展的瓶颈。你是否也面临这样的挑战:代码库臃肿不堪、发布周期越来越长、局部故障导致全局瘫痪、技术栈升级举步维艰?作为一名有8年开发经验的Java工程师,我曾主导多个大型电商系统的微服务拆分。今天我将分享从业务
- 如何设计一个社交平台的关注/粉丝系统?一位8年Java开发者的架构心路
天天摸鱼的java工程师
java架构开发语言
如何设计一个社交平台的关注/粉丝系统?——一位8年Java开发者的架构心路当你的社交平台面临百万用户实时互动,如何确保关注操作毫秒级响应?如何保证粉丝列表的实时性和一致性?这个看似基础的功能背后,隐藏着读写扩散、数据一致性、热点用户等架构难题。本文将带你从业务模型到代码落地,构建一个支撑千万级关系的社交系统。一、业务场景与核心挑战典型关注业务流程:未关注已关注用户A关注用户B关系检查写入关注关系更
- junit mockito_如何学习Java中的单元测试:JUnit和Mockito课程
dfsgwe1231
单元测试编程语言python人工智能java
junitmockito大家好,今天我将讨论JUnit和单元测试,这是任何软件开发人员的关键技能之一。您可能已经知道JUnit和Mockito是Java应用程序中最受欢迎的两个测试库,并且几乎在每个Java应用程序类路径中都可以找到它们。我经常与Java开发人员见面并一起工作,这些Java开发人员非常了解Java但还没有编写单个单元测试。当我问他们为什么不编写单元测试时,他们提出了许多借口,例如他
- (二十三)Java反射机制深度解析:原理、应用与最佳实践
MeyrlNotFound
JAVA开发语言java
一、反射机制概述1.1什么是反射机制Java反射机制(Reflection)是Java语言中一种强大的内省(introspection)能力,它允许程序在运行时(runtime)获取类的内部信息,并能直接操作类或对象的内部属性及方法。这种"动态性"使得Java程序可以突破编译时的限制,实现许多灵活的功能。反射的核心思想是:在运行时而非编译时获取类型信息并执行操作。这与传统的静态编程形成鲜明对比,在
- 【ASP.NET Core】ASP.NET Core中Redis分布式缓存的应用
ArabySide
#.NETCoreRedis缓存redis分布式缓存asp.netasp.netcore
系列文章目录链接:【ASP.NETCore】REST与RESTful详解,从理论到实现链接:【ASP.NETCore】深入理解Controller的工作机制链接:【ASP.NETCore】内存缓存(MemoryCache)原理、应用及常见问题解析文章目录系列文章目录前言一、Redis1.1Redis简介1.2常用数据结构1.3Redis的持久化1.3.1RDB1.3.2AOF1.4常用应用场景1.
- ubuntu18.04安装geemap
阿西是有梦想的咸鱼
python编程之路遥感影像处理可视化可视化pythonubuntu
文章目录安装测试GEE提供了JavaScript和PythonAPI,可以向EarthEngine服务器发出计算请求。与GEEJavaScriptAPI相比,PythonAPI缺乏易于理解的操作文档和交互式可视化结果的功能。由此,geemap诞生并填补了这一空白[1]。这里给大家介绍下我折腾了一晚上才搞定的geemap的安装及测试过程。这里是geemap的GitHub参考链接。安装如Github中
- java list使用
奋斗live
一、增加、删除、查询可使用add、remove、get方法,如下System.out.println("list的添加、获取和删除元素");Listanimal=newArrayListanimal=newArrayListanimal=newArrayListanimal=newArrayListanimal=newArrayListanimal=newArrayListphone=newArr
- JUC——创建线程的方法
机器滴小白
JAVA学习笔记java开发语言JUC并发编程
1.继承Thread类原理:通过继承Thread类并重写其run()方法,定义线程的执行逻辑。(Thread类实现了Runnable接口)调用start()方法启动线程(JVM会自动调用run())。特点简单直接,适合快速实现线程逻辑。局限性:Java是单继承的,继承Thread后无法再继承其他类。//1.继承Thread类classMyThreadextendsThread{@Overridep
- java 结合 FreeMarker 和 Docx4j 来生成包含图片的 docx 文件
liangblog
Java生产环境全栈开发Java进阶javapython开发语言
使用FreeMarker生成HTML,然后通过Docx4j将HTML转换为.docx文件;步骤1.添加依赖确保你的项目中包含了FreeMarker和Docx4j的依赖。以下是Maven的pom.xml示例:
- 前端实现多文件下载功能的思路与代码分享
好运仔dzl
技术开发java开发语言
73万字的Java面试题库【全网最详细-找工作/实习必备神器】:https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzE5MTY1NzczOA==&action=getalbum&album_id=4057608455186808839Java面试题库ps:网上面试题多而杂,自己整理了一套面试题,我靠这套面试题2年经验拿15k~前端实现多文件下载功能的思路
- 如何在 Stimulsoft JavaScript 报表组件中,设置设计器与查看器主题风格
CodeCraft Studio
控件报表图表开发javascript开发语言ecmascriptStimulsoftDashboardReport报表仪表盘工具
在现代软件开发中,图形用户界面(GUI)不仅仅是功能的承载体,更是用户体验的关键组成部分。一个美观、统一且具备高度可定制性的界面,能够显著提升系统的专业感和使用效率。Stimulsoft作为功能强大的报表和仪表板解决方案提供商,其JavaScript版本(StimulsoftReports.JS与StimulsoftDashboards.JS)为开发者提供了丰富的内置主题支持,助力快速构建符合品牌
- [Java实战]Spring Boot 整合 Freemarker (十一)
曼岛_
Java实战javaspringboot开发语言
[Java实战]SpringBoot整合Freemarker(十一)引言ApacheFreeMarker作为一款高性能的模板引擎,凭借其简洁语法、卓越性能和灵活扩展性,在JavaWeb开发中占据重要地位。结合SpringBoot的自动化配置能力,开发者能快速构建动态页面、生成报表或定制代码。本文将系统讲解整合流程、实战技巧、性能优化方案,并针对企业级场景提供深度解决方案。一、Freemarker核
- Blazor使用TXTextControl控件编辑报告
落叶飞花_
javascript开发语言
文章目录1环境2课程链接3学习使用(加载TextControl控件)3.1DocumentEditor3.2DocumentViewer4javascriptApi列表5加载文档(TextControl加载文档,JS互操作)6开启修改跟踪(word中的修订)7文档修改保存8文档编辑,拖拽展示图片9文档编辑,使用ApplicationField10模板设计11插入图片11.1拖拽插入图片11.2Me
- Java线程池
Executor接口Executor接口是线程池的基类,基本上所有的线程池类都直接或间接继承此类。接口定义publicinterfaceExecutor{voidexecute(Runnablecommand);}ExecutorService接口接口定义ExecutorService接口继承自Executor接口。publicinterfaceExecutorServiceextendsExec
- Java 原生 HTTP Client
en-route
微服务之间如何调用javahttp开发语言
介绍Java原生HttpClient是从Java11开始引入的标准库,用于简化HTTP请求的发送与响应处理。它支持同步和异步请求,并内置对HTTP/1.1和HTTP/2协议的支持。HttpClient提供了易用的API来设置请求头、请求体、处理响应以及配置SSL/TLS加密等安全功能。一个简单的例子发送GET请求并将打印ResponseHttpClientclient=HttpClient.new
- 如何用 Mockito 玩转单元测试
en-route
单元测试
介绍Mockito是一个广泛使用的Java测试框架,它提供了简洁而强大的功能,用于模拟(mock)和验证对象的行为,尤其是在单元测试中。当我们需要测试某个类的功能时,但又不希望依赖其外部组件或复杂的对象时,可以使用Mockito来创建模拟对象,这些模拟对象可以控制方法返回值、抛出异常或执行特定的逻辑。Mockito使得测试变得更加独立、可靠和可维护,特别是在测试依赖较多或外部系统交互的代码时。从一
- 重塑未来:AI如何重新定义全栈开发
熊猫钓鱼>_>
人工智能
在传统认知中,全栈开发者被誉为技术界的“全能选手”。——他们需要精通前端界面构建(HTML/CSS/JavaScript)、后端业务逻辑实现(Python/Java/Node.js)、数据库设计优化(MySQL/MongoDB)以及服务器部署运维(Linux/Docker)。这种“一人包打天下”的能力模型长期被视为高效开发的黄金标准,尤其受到创业公司和小型团队的青睐,因为它能大幅减少沟通成本,加速
- Javascript 严格模式use strict详解
滴水成川
JavaScript学习记录javascriptusestrict
一、概述除了正常运行模式,ECMAscript5添加了第二种运行模式:"严格模式"(strictmode)。顾名思义,这种模式使得Javascript在更严格的条件下运行。设立"严格模式"的目的,主要有以下几个:-消除Javascript语法的一些不合理、不严谨之处,减少一些怪异行为;-消除代码运行的一些不安全之处,保证代码运行的安全;-提高编译器效率,增加运行速度;-为未来新版本的Javascr
- 函数调用栈回溯机制详解
硬核科技
嵌入式单片机开发实战嵌入式嵌入式硬件软件单片机
函数调用回溯Backtrace是现代软件系统调试中的关键技术之一,尤其在嵌入式开发和Linux平台调试中更显重要。它提供了程序在运行或崩溃时的函数调用路径,有助于快速定位错误源。一、函数调用栈与Backtrace的理论基础1.1什么是函数调用栈?函数调用栈(CallStack)是一种由编译器和运行时系统共同维护的后进先出(LIFO)数据结构。每次函数调用时,当前函数的返回地址、局部变量、保存的寄存
- List和Map的区别
雪碧聊技术
Java八股文list数据结构
欢迎来到我的Java八股文专栏!各位程序员小伙伴们好呀~我是雪碧聊技术,很高兴能在CSDN与大家相遇!✨专栏介绍这个专栏将专注于分享Java面试中的经典"八股文"知识点,内容涵盖:Java基础核心概念JVM原理与性能调优多线程与并发编程️设计模式实战️常用框架源码解析⚙️系统架构设计思想为什么选择这个专栏?精准定位:直击大厂Java面试高频考点系统全面:从基础到进阶,构建完整知识体系实战导向:理论
- 【面试】面试官:请介绍一下你如何高效处理海量数据与JVM内存故障排查方法?
文章目录高效处理海量数据与JVM内存分析实战指南问题一:无内存限制下如何快速安全插入1000亿条数据到HashMap?1.数据结构优化2.内存与IO协同优化3.业务级安全策略问题二:JVM内存分析与OOM故障排查1.实时内存占用分析2.OOM事后分析流程步骤1:获取诊断三件套步骤2:定位泄漏根源步骤3:业务防御机制架构启示录高效处理海量数据与JVM内存分析实战指南问题一:无内存限制下如何快速安全插
- 领域驱动设计精要
我是廖志伟
Java场景面试宝典DDDDomain-DrivenDesignSoftwareArchitecture
我是廖志伟,一名Java开发工程师、《Java项目实战——深入理解大型互联网企业通用技术》(基础篇)、(进阶篇)、(架构篇)、《解密程序员的思维密码——沟通、演讲、思考的实践》作者、清华大学出版社签约作家、Java领域优质创作者、CSDN博客专家、阿里云专家博主、51CTO专家博主、产品软文专业写手、技术文章评审老师、技术类问卷调查设计师、幕后大佬社区创始人、开源项目贡献者。拥有多年一线研发和团队
- DDD核心知识解析
我是廖志伟
Java场景面试宝典DDDSoftwareDesignBusinessLogic
我是廖志伟,一名Java开发工程师、《Java项目实战——深入理解大型互联网企业通用技术》(基础篇)、(进阶篇)、(架构篇)、《解密程序员的思维密码——沟通、演讲、思考的实践》作者、清华大学出版社签约作家、Java领域优质创作者、CSDN博客专家、阿里云专家博主、51CTO专家博主、产品软文专业写手、技术文章评审老师、技术类问卷调查设计师、幕后大佬社区创始人、开源项目贡献者。拥有多年一线研发和团队
- ShardingSphere核心机制解析
我是廖志伟
Java场景面试宝典DatabaseMiddlewareDistributedDatabaseShardingSphere
我是廖志伟,一名Java开发工程师、《Java项目实战——深入理解大型互联网企业通用技术》(基础篇)、(进阶篇)、(架构篇)、《解密程序员的思维密码——沟通、演讲、思考的实践》作者、清华大学出版社签约作家、Java领域优质创作者、CSDN博客专家、阿里云专家博主、51CTO专家博主、产品软文专业写手、技术文章评审老师、技术类问卷调查设计师、幕后大佬社区创始人、开源项目贡献者。拥有多年一线研发和团队
- JVM与Spring Boot核心解析
我是廖志伟
Java场景面试宝典JavaJVMSpringBoot
我是廖志伟,一名Java开发工程师、《Java项目实战——深入理解大型互联网企业通用技术》(基础篇)、(进阶篇)、(架构篇)清华大学出版社签约作家、Java领域优质创作者、CSDN博客专家、阿里云专家博主、51CTO专家博主、产品软文专业写手、技术文章评审老师、技术类问卷调查设计师、幕后大佬社区创始人、开源项目贡献者。拥有多年一线研发和团队管理经验,研究过主流框架的底层源码(Spring、Spri
- 领域驱动设计(DDD)实践解析
我是廖志伟,一名Java开发工程师、《Java项目实战——深入理解大型互联网企业通用技术》(基础篇)、(进阶篇)、(架构篇)清华大学出版社签约作家、Java领域优质创作者、CSDN博客专家、阿里云专家博主、51CTO专家博主、产品软文专业写手、技术文章评审老师、技术类问卷调查设计师、幕后大佬社区创始人、开源项目贡献者。拥有多年一线研发和团队管理经验,研究过主流框架的底层源码(Spring、Spri
- java线程的无限循环和退出
3213213333332132
java
最近想写一个游戏,然后碰到有关线程的问题,网上查了好多资料都没满足。
突然想起了前段时间看的有关线程的视频,于是信手拈来写了一个线程的代码片段。
希望帮助刚学java线程的童鞋
package thread;
import java.text.SimpleDateFormat;
import java.util.Calendar;
import java.util.Date
- tomcat 容器
BlueSkator
tomcatWebservlet
Tomcat的组成部分 1、server
A Server element represents the entire Catalina servlet container. (Singleton) 2、service
service包括多个connector以及一个engine,其职责为处理由connector获得的客户请求。
3、connector
一个connector
- php递归,静态变量,匿名函数使用
dcj3sjt126com
PHP递归函数匿名函数静态变量引用传参
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>Current To-Do List</title>
</head>
<body>
- 属性颜色字体变化
周华华
JavaScript
function changSize(className){
var diva=byId("fot")
diva.className=className;
}
</script>
<style type="text/css">
.max{
background: #900;
color:#039;
- 将properties内容放置到map中
g21121
properties
代码比较简单:
private static Map<Object, Object> map;
private static Properties p;
static {
//读取properties文件
InputStream is = XXX.class.getClassLoader().getResourceAsStream("xxx.properti
- [简单]拼接字符串
53873039oycg
字符串
工作中遇到需要从Map里面取值拼接字符串的情况,自己写了个,不是很好,欢迎提出更优雅的写法,代码如下:
import java.util.HashMap;
import java.uti
- Struts2学习
云端月影
最近开始关注struts2的新特性,从这个版本开始,Struts开始使用convention-plugin代替codebehind-plugin来实现struts的零配置。
配置文件精简了,的确是简便了开发过程,但是,我们熟悉的配置突然disappear了,真是一下很不适应。跟着潮流走吧,看看该怎样来搞定convention-plugin。
使用Convention插件,你需要将其JAR文件放
- Java新手入门的30个基本概念二
aijuans
java新手java 入门
基本概念: 1.OOP中唯一关系的是对象的接口是什么,就像计算机的销售商她不管电源内部结构是怎样的,他只关系能否给你提供电就行了,也就是只要知道can or not而不是how and why.所有的程序是由一定的属性和行为对象组成的,不同的对象的访问通过函数调用来完成,对象间所有的交流都是通过方法调用,通过对封装对象数据,很大限度上提高复用率。 2.OOP中最重要的思想是类,类是模板是蓝图,
- jedis 简单使用
antlove
javarediscachecommandjedis
jedis.RedisOperationCollection.java
package jedis;
import org.apache.log4j.Logger;
import redis.clients.jedis.Jedis;
import java.util.List;
import java.util.Map;
import java.util.Set;
pub
- PL/SQL的函数和包体的基础
百合不是茶
PL/SQL编程函数包体显示包的具体数据包
由于明天举要上课,所以刚刚将代码敲了一遍PL/SQL的函数和包体的实现(单例模式过几天好好的总结下再发出来);以便明天能更好的学习PL/SQL的循环,今天太累了,所以早点睡觉,明天继续PL/SQL总有一天我会将你永远的记载在心里,,,
函数;
函数:PL/SQL中的函数相当于java中的方法;函数有返回值
定义函数的
--输入姓名找到该姓名的年薪
create or re
- Mockito(二)--实例篇
bijian1013
持续集成mockito单元测试
学习了基本知识后,就可以实战了,Mockito的实际使用还是比较麻烦的。因为在实际使用中,最常遇到的就是需要模拟第三方类库的行为。
比如现在有一个类FTPFileTransfer,实现了向FTP传输文件的功能。这个类中使用了a
- 精通Oracle10编程SQL(7)编写控制结构
bijian1013
oracle数据库plsql
/*
*编写控制结构
*/
--条件分支语句
--简单条件判断
DECLARE
v_sal NUMBER(6,2);
BEGIN
select sal into v_sal from emp
where lower(ename)=lower('&name');
if v_sal<2000 then
update emp set
- 【Log4j二】Log4j属性文件配置详解
bit1129
log4j
如下是一个log4j.properties的配置
log4j.rootCategory=INFO, stdout , R
log4j.appender.stdout=org.apache.log4j.ConsoleAppender
log4j.appender.stdout.layout=org.apache.log4j.PatternLayout
log4j.appe
- java集合排序笔记
白糖_
java
public class CollectionDemo implements Serializable,Comparable<CollectionDemo>{
private static final long serialVersionUID = -2958090810811192128L;
private int id;
private String nam
- java导致linux负载过高的定位方法
ronin47
定位java进程ID
可以使用top或ps -ef |grep java
![图片描述][1]
根据进程ID找到最消耗资源的java pid
比如第一步找到的进程ID为5431
执行
top -p 5431 -H
![图片描述][2]
打印java栈信息
$ jstack -l 5431 > 5431.log
在栈信息中定位具体问题
将消耗资源的Java PID转
- 给定能随机生成整数1到5的函数,写出能随机生成整数1到7的函数
bylijinnan
函数
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class RandNFromRand5 {
/**
题目:给定能随机生成整数1到5的函数,写出能随机生成整数1到7的函数。
解法1:
f(k) = (x0-1)*5^0+(x1-
- PL/SQL Developer保存布局
Kai_Ge
近日由于项目需要,数据库从DB2迁移到ORCAL,因此数据库连接客户端选择了PL/SQL Developer。由于软件运用不熟悉,造成了很多麻烦,最主要的就是进入后,左边列表有很多选项,自己删除了一些选项卡,布局很满意了,下次进入后又恢复了以前的布局,很是苦恼。在众多PL/SQL Developer使用技巧中找到如下这段:
&n
- [未来战士计划]超能查派[剧透,慎入]
comsci
计划
非常好看,超能查派,这部电影......为我们这些热爱人工智能的工程技术人员提供一些参考意见和思想........
虽然电影里面的人物形象不是非常的可爱....但是非常的贴近现实生活....
&nbs
- Google Map API V2
dai_lm
google map
以后如果要开发包含google map的程序就更麻烦咯
http://www.cnblogs.com/mengdd/archive/2013/01/01/2841390.html
找到篇不错的文章,大家可以参考一下
http://blog.sina.com.cn/s/blog_c2839d410101jahv.html
1. 创建Android工程
由于v2的key需要G
- java数据计算层的几种解决方法2
datamachine
javasql集算器
2、SQL
SQL/SP/JDBC在这里属于一类,这是老牌的数据计算层,性能和灵活性是它的优势。但随着新情况的不断出现,单纯用SQL已经难以满足需求,比如: JAVA开发规模的扩大,数据量的剧增,复杂计算问题的涌现。虽然SQL得高分的指标不多,但都是权重最高的。
成熟度:5星。最成熟的。
- Linux下Telnet的安装与运行
dcj3sjt126com
linuxtelnet
Linux下Telnet的安装与运行 linux默认是使用SSH服务的 而不安装telnet服务 如果要使用telnet 就必须先安装相应的软件包 即使安装了软件包 默认的设置telnet 服务也是不运行的 需要手工进行设置 如果是redhat9,则在第三张光盘中找到 telnet-server-0.17-25.i386.rpm
- PHP中钩子函数的实现与认识
dcj3sjt126com
PHP
假如有这么一段程序:
function fun(){
fun1();
fun2();
}
首先程序执行完fun1()之后执行fun2()然后fun()结束。
但是,假如我们想对函数做一些变化。比如说,fun是一个解析函数,我们希望后期可以提供丰富的解析函数,而究竟用哪个函数解析,我们希望在配置文件中配置。这个时候就可以发挥钩子的力量了。
我们可以在fu
- EOS中的WorkSpace密码修改
蕃薯耀
修改WorkSpace密码
EOS中BPS的WorkSpace密码修改
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 201
- SpringMVC4零配置--SpringSecurity相关配置【SpringSecurityConfig】
hanqunfeng
SpringSecurity
SpringSecurity的配置相对来说有些复杂,如果是完整的bean配置,则需要配置大量的bean,所以xml配置时使用了命名空间来简化配置,同样,spring为我们提供了一个抽象类WebSecurityConfigurerAdapter和一个注解@EnableWebMvcSecurity,达到同样减少bean配置的目的,如下:
applicationContex
- ie 9 kendo ui中ajax跨域的问题
jackyrong
AJAX跨域
这两天遇到个问题,kendo ui的datagrid,根据json去读取数据,然后前端通过kendo ui的datagrid去渲染,但很奇怪的是,在ie 10,ie 11,chrome,firefox等浏览器中,同样的程序,
浏览起来是没问题的,但把应用放到公网上的一台服务器,
却发现如下情况:
1) ie 9下,不能出现任何数据,但用IE 9浏览器浏览本机的应用,却没任何问题
- 不要让别人笑你不能成为程序员
lampcy
编程程序员
在经历六个月的编程集训之后,我刚刚完成了我的第一次一对一的编码评估。但是事情并没有如我所想的那般顺利。
说实话,我感觉我的脑细胞像被轰炸过一样。
手慢慢地离开键盘,心里很压抑。不禁默默祈祷:一切都会进展顺利的,对吧?至少有些地方我的回答应该是没有遗漏的,是不是?
难道我选择编程真的是一个巨大的错误吗——我真的永远也成不了程序员吗?
我需要一点点安慰。在自我怀疑,不安全感和脆弱等等像龙卷风一
- 马皇后的贤德
nannan408
马皇后不怕朱元璋的坏脾气,并敢理直气壮地吹耳边风。众所周知,朱元璋不喜欢女人干政,他认为“后妃虽母仪天下,然不可使干政事”,因为“宠之太过,则骄恣犯分,上下失序”,因此还特地命人纂述《女诫》,以示警诫。但马皇后是个例外。
有一次,马皇后问朱元璋道:“如今天下老百姓安居乐业了吗?”朱元璋不高兴地回答:“这不是你应该问的。”马皇后振振有词地回敬道:“陛下是天下之父,
- 选择某个属性值最大的那条记录(不仅仅包含指定属性,而是想要什么属性都可以)
Rainbow702
sqlgroup by最大值max最大的那条记录
好久好久不写SQL了,技能退化严重啊!!!
直入主题:
比如我有一张表,file_info,
它有两个属性(但实际不只,我这里只是作说明用):
file_code, file_version
同一个code可能对应多个version
现在,我想针对每一个code,取得它相关的记录中,version 值 最大的那条记录,
SQL如下:
select
*
- VBScript脚本语言
tntxia
VBScript
VBScript 是基于VB的脚本语言。主要用于Asp和Excel的编程。
VB家族语言简介
Visual Basic 6.0
源于BASIC语言。
由微软公司开发的包含协助开发环境的事
- java中枚举类型的使用
xiao1zhao2
javaenum枚举1.5新特性
枚举类型是j2se在1.5引入的新的类型,通过关键字enum来定义,常用来存储一些常量.
1.定义一个简单的枚举类型
public enum Sex {
MAN,
WOMAN
}
枚举类型本质是类,编译此段代码会生成.class文件.通过Sex.MAN来访问Sex中的成员,其返回值是Sex类型.
2.常用方法
静态的values()方