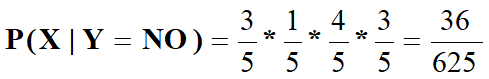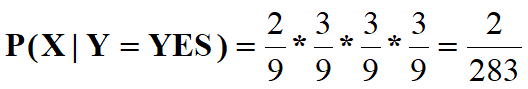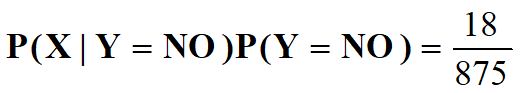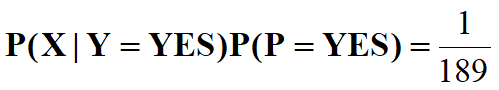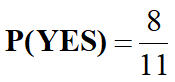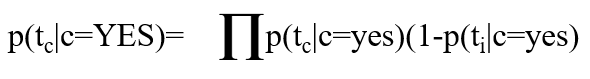机器学习---初识贝叶斯分类器

1. 引入问题

有两个可选的假设：病人有癌症、病人无癌症，可用数据来自化验结果：正+和负-

有先验知识：在所有人口中，患病率是0.008，对确实有病的患者的化验准确率为98%，对确实无

病的患者的化验准确率为97%

总结如下：

P(cancer)=0.008, P(┐cancer)=0.992

P(+|cancer)=0.98, P(-|cancer)=0.02

P(+|┐cancer)=0.03, P(-|┐cancer)=0.9

问题：假定有一个新病人，化验结果为正，是否应将病人断定为有癌症？求后验概率P(cancer|+)

和P(┐cancer|+)

解决上面的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况

下如何求得P(B|A)。

A：判断准确    B：癌症

条件概率： 在事情B发生的条件下A发生的条件概率，其求解公式为：

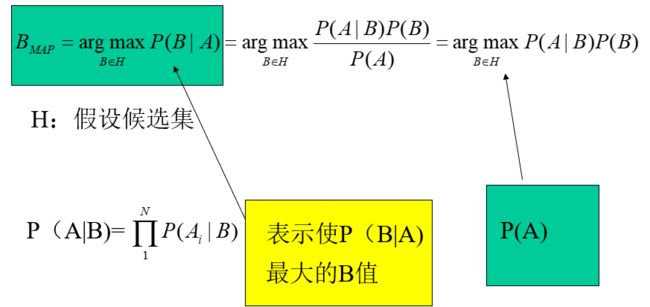
贝叶斯定理的意义在于，在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则

很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

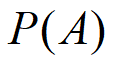 ：表示在没有训练数据前假设A拥有的初始概率，P(A)被称为A的先验概率。

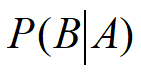：P(A|B)表示假设B成立时A的概率。机器学习中我们关心的是P(B|A)，即给定A时B的成

立的概率，称为B的后验概率。

 P(B|A)随着P(B)和P(A|B)的增长而增长，随着P(A)的增长而减少，即如果A独立于B时被观察到的

可能性越大，那么B对A的支持度越小。

2. 朴素贝叶斯分类器

条件独立性：给定类标号y，朴素贝叶斯分类器在估计类条件概率时假设属性之间条件独立。条件

独立假设可以形式化的表达如下：

其中每个训练样本可用一个属性向量X=(x1,x2,x3,„,xn)表示，各个属性之间条件独立。

比如，对于一篇文章“Good good study,Day day up.”

用一个文本特征向量来表示：x=(Good, good, study, Day, day , up)。

一般各个词语之间肯定不是相互独立的，有一定的上下文联系。但在朴素贝叶斯文本分类时，我们

假设个单词之间没有联系，可以用一个文本特征向量来表示这篇文章，这就是“朴素”的来历。

有了条件独立假设，就不必计算X和Y的每一种组合的类条件概率，只需对给定的Y，计算每个xi的

条件概率。后一种方法更实用，因为它不需要很大的训练集就能获得较好的概率估计。

P(xi|Y=y)怎么计算呢？它一般根据类别y下包含属性xi的实例的比例来估计。以文本分类为例，xi表

示一个单词，P(xi|Y=y)=包含该类别下包含单词的xi的文章总数/ 该类别下的文章总数。

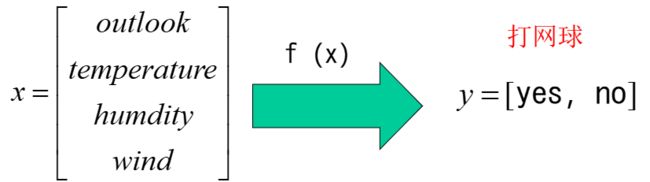
假设给定了如下训练样本数据，我们学习的目标是根据给定的天气状况判断你对PlayTennis这个请

求的回答是Yes还是No。

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mild	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	Strong	Yes
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes
D14	Rain	Mild	High	Strong	No

         

我们需要利用训练数据计算后验概率P(Yes|x)和P(No|x)，如果P(Yes|x)>P(No|x)，那么新实例分类

为Yes，否则为No。 

我们将使用此表的数据，并结合朴素贝叶斯分类器来分类下面的新实例：

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D8	Sunny	Mild	High	Weak	No
D14	Rain	Mild	High	Strong	No
D6	Rain	Cool	Normal	Strong	No

      

   

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mild	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D7	Overcast	Cool	Normal	Strong	Yes
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes

           

由于 大于所以该样本分类为No

3. 多项式模型

基本原理：多项式模型中， 设某文档d=(t1,t2,…,tk)，tk是该文档中出现过的单词，允许重复，则:

V是训练样本的单词表（即抽取单词，单词出现多次，只算一个），|V|则表示训练样本包含多少种

单词。在这里，m=|V|, p=1/|V|。P( tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据，

而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。

给定一个新样本Chinese Chinese Chinese Tokyo Japan，对其进行分类：

该文本用属性向量表示为d=(Chinese, Chinese, Chinese, Tokyo, Japan)，类别集合为Y={yes,

no}。                

id	doc	类别In c=China?
1	Chinese Beijing Chinese	yes
2	Chinese Chinese Shanghai	yes
3	Chinese Macao	yes
4	Tokyo Japan Chinese	no

P(Japan | yes)=P(Tokyo | yes)= (0+1)/(8+6)=1/14

P(Chinese | yes)=(5+1)/(8+6)=6/14=3/7

P(Chinese|no)=(1+1)/(3+6)=2/9

P(Japan|no)=P(Tokyo| no) =(1+1)/(3+6)=2/9

p(yes|d)=(3/7)3×1/14×1/14×8/11=108/184877≈0.00058417

P(no|d)= (2/9)3×2/9×2/9×3/11=32/216513≈0.00014780

因此，这个文档属于类别china。

4. 伯努利模型

基本原理：

id	doc	类别In c=China?
1	Chinese Beijing Chinese	yes
2	Chinese Chinese Shanghai	yes
3	Chinese Macao	yes
4	Tokyo Japan Chinese	no

P(Chinese|yes)=(3+1)/(3+2)=4/5

P(Beijing|yes)= P(Macao|yes)= P(Shanghai |yes)=(1+1)/(3+2)=2/5

P(Japan | yes)=P(Tokyo | yes)=(0+1)/(3+2)=1/5

P(Chinese|no)=(1+1)/(1+2)=2/3

 P(Japan|no)=P(Tokyo| no) =(1+1)/(1+2)=2/3

P(Beijing|no)= P(Macao|no)= P(Shanghai|no)=(0+1)/(1+2)=1/3

P(yes | d)=P(yes)×P(Chinese|yes) ×P(Japan|yes) ×P(Tokyo|yes)×(1-P(Beijing|yes)) ×(1-

P(Shanghai|yes))×(1-P(Macao|yes))=3/4×4/5×1/5×1/5×(1-2/5) ×(1-2/5)×(1-2/5)=81/15625≈0.005

P(no | d)= 1/4×2/3×2/3×2/3×(1-1/3)×(1-1/3)×(1-1/3)=16/729≈0.022

因此，这个文档不属于类别china。

        二者的计算粒度不一样，多项式模型以单词为粒度，伯努利模型以文件为粒度，因此二者的

先验概率和类条件概率的计算方法都不同。计算后验概率时，对于一个文档d，多项式模型中，只

有在d中出现过的单词，才会参与后验概率计算。伯努利模型中，没有在d中出现，但是在全局单词

表中出现的单词，也会参与计算，不过是作为“反方”参与。