基础算法杂例-差分

引入

• 承接前缀和，差分是前缀和的逆运算，典型题目：对若干数据进行区间内的加减。

问题来了，那这个操作如果暴力遍历进行加减的话，也只是 O（n） 的复杂度，如果对数据进行m组操作，也只是会变成 O(mn) 。 所以没必要学差分，文章到此结束 当然有必要，研究差分的目的就是为了让复杂度“从O（n）到O（1） ”。接下来我将主要以题目引入差分的代码实现。

一维差分

上边说到，差分是前缀和的逆运算，所以，差分数组的前缀和就是原数组，即

首先给定一个原数组a：

然后我们构造差分数组b ：

使得 a[n] = b[1] + b[2] + b[3] + , + b[n]；

很明显，利用基本的数学方法就能得到差分数组的初始化方式：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

…
b[n] = a[n] - a[n - 1];

那我们得到这个数组怎么对一个区间就进行操作呢？

我们先想，差分数组就是每两项之间的差值
那如果这个差分数组，在某个点 i 突然增加5，那这点紧邻的那个点(j = i +1)就会增加5

但是点 j 和他下个点 k之间的差值并没有改变，所以k也得加5，

以此类推，之后的所有值都得加上5，就像影院第一排的人站了起来最后所有人都站了起来。

那这样可不行，我们只需要一个限定范围增加c。那我让右边界点之后的点在减去c，不就能达到我们的效果了吗。

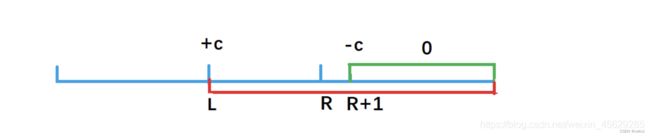
划重点！
所以就能得到通用公式:
给a数组中的[ l, r] 区间中的每一个数都加上c

b[l] + = c;
b[r+1] - = c ;

这个结论还可以用来构造差分数组，
在遍历a数组时，我们可以当做是一个全部为0的数组，然后fori去遍历a数组，不断在[i,i] 这个区间内，加上 a[i]

题目与代码实现

以下为AC代码：

#include 
using namespace std;

int a[100010], b[100010];
int main() {
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		b[i] = a[i] - a[i - 1];   
	}
	int l, r, c;
	while(m--) {
		scanf("%d%d%d", &l, &r, &c);
		b[l] += c;
		b[r + 1] -= c;
	}
	for(int i = 1; i <= n; i++) {
		b[i] += b[i - 1];
		printf("%d ", b[i]);
	}
}

二维差分

• 二维差分的思想和二维前缀和的思想一致。

我们主要的操作还是对一段固定的区间进行加减，从一维到二维，暴力解法的复杂度会是 O(n*n)，但利用差分我们还是可以用O(1) 的复杂度可以解决。
假设我们需要在 A（x1,y1）和B（x2,y2）之间的所有数据进行操作。有了一维差分的经验，我们很容易想到先让A之后的所有数据进行操作，再进行“修剪”。
即

b[x1][y1] += c;

此时情况会如图示：

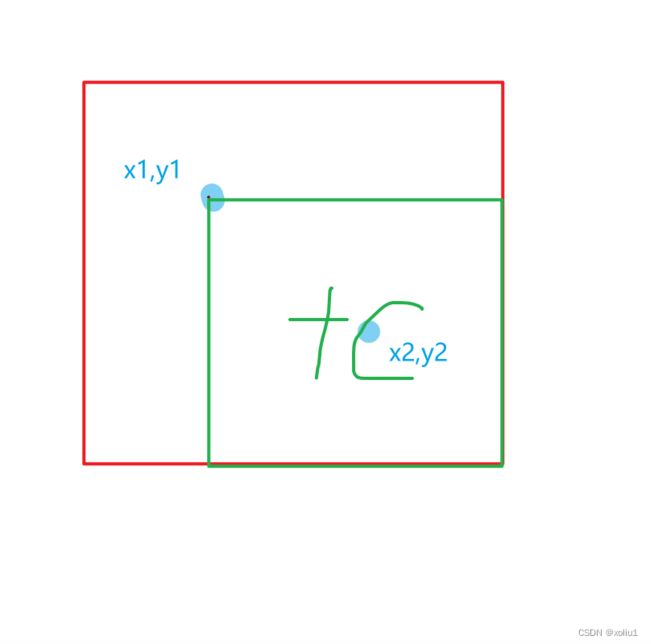
很明显我们能看到在A之后的范围都会 +c ，这不是我们希望看到的。

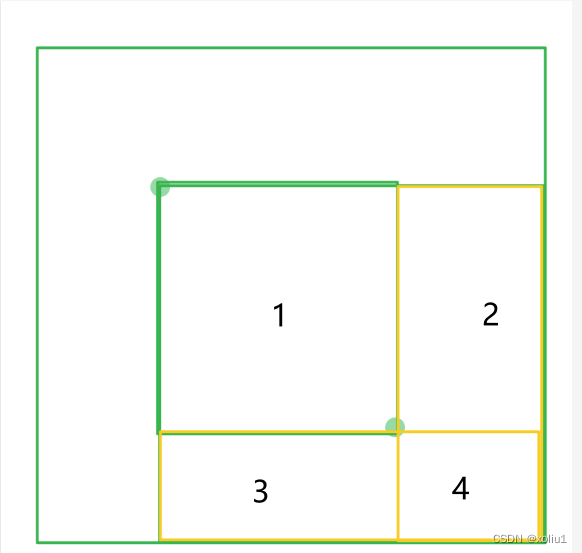
刚刚的操作我们让1 2 3 4都加c ，现在我们可以让3 4 减c，然后2 4减c，2 3就平衡了，然后4在单独加c，就能达到效果

即：

void insert(int x1,int y1,int x2,int y2,int c){  
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

• 同样的道理，这个也可以用来构造二维差分数组，不再赘述。

题目与代码实现

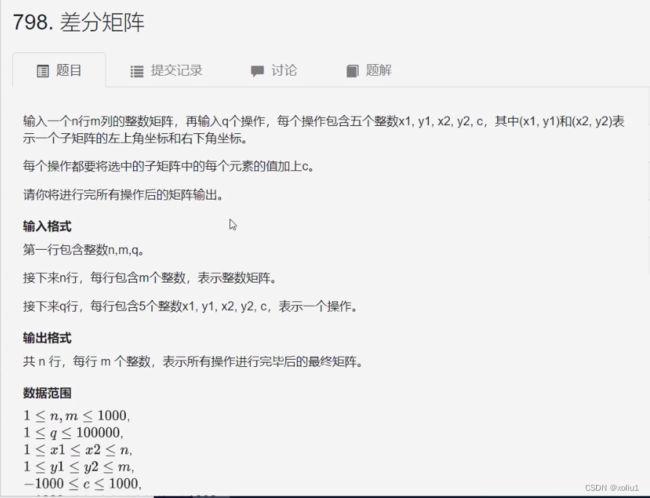
与一维的操作大同小异，仅insert函数有所变动，故在此进行赘述
在此附上AC代码

#include 
using namespace std;

int a[1001][1001],b[1001][1001]; 
void insert(int x1, int y1, int x2, int y2, int c) {
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}
int main() {
	int n, m, q;
	cin >> n >> m >> q;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			cin >> a[i][j];
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			insert(i, j, i, j, a[i][j]);
		}
	}
	while (q--) {
		int x1, y1, x2, y2, c;
		cin >> x1 >> y1 >> x2 >> y2 >> c;
		insert(x1, y1, x2, y2, c);
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			printf("%d ", b[i][j]);
		}
		printf("\n");
	}
}

谢谢！