最长回文子串与最长回文子序列

两道经典的动态规划题

最长回文子串
最长回文子序列

基础概念

回文 (Palindrome)

回文，指正读反读都能读懂的句子，如“我为人人，人人为我”等。在数学中也有这样一类数字有这样的特征，称为回文数（palindrome number），如n=1234321。

回文字符串:即"aba","cdfgfdc"这种正读反读都相同的字符串

子串和子序列

子串和子序列都属于原字符串的一部分，不过结构略有不同。例：如"asdfgh"
子串：“asd"或"fgh”，字符组合在原字符串是连续的
子序列：“afh”，字符组合不连续，但每个字符都属于原字符串，且有序。

如何验证是否是回文串？

首先验证字符串的第一个字符和最后一个字符。
1）如果这两个字符不相同，则这个字符串一定不是回文串。
2）如果这两个字符相同，则继续验证起点的下一个字符以及终点的上一个字符，不断验证下去。
不断的更新起点字符和终点字符，直到起点位置大于等于终点位置，结束验证，证明整个字符串是回文串。

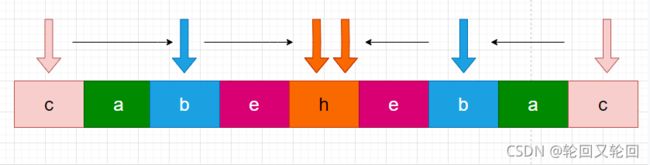
一旦在验证过程中有字符不相同，说明整个字符串都不是回文串

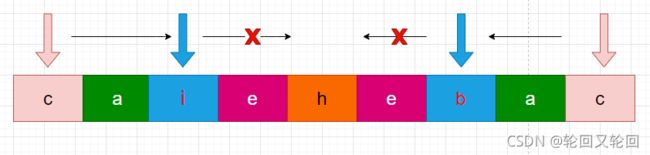
代码：

//递归
public boolean longestPalindrome(String s){
	int n = s.length();
	return checkPalindrome(s,0,n-1);
}

public boolean checkPalindrome(String s, int start, int end){
	if(start >= end){
		return true;
	}
	if(s.charAt(start)==s.charAt(end){
		return checkPalindrome(s,start+1,end-1);
	}
	return false;
}

leetcode5：最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

解法一：暴力解法-递归

暴力解法：先保持起点坐标不变，不断变化终点坐标，验证每个相同起点坐标与不同终点坐标组成的字符串是否是回文串。当终点坐标等于字符串长度时，更新起点坐标，再重复上述操作。记录最大长度的回文串。

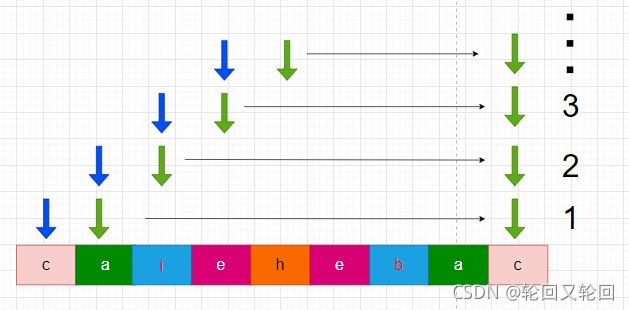
int start;
int len;
public boolean longestPalindromeSubstring(String s){
	int n = s.length();
	start = 0;
	len = 0;
	for(int i = 0; i < n; i++){	
		for(int j = i; j < n; j++){
		//验证第i个字符到第j个字符组成的字符串是否是回文串
		//如果是回文串，则验证是否更新了已记录的最长记录
			if(checkPalindrome(s,i,j)){
				if(j-i+1 > len){
					len = j - i + 1;
					start = i;
				}
			}
		}	
	}
	return s.substring(start,start+len);
}

暴力解法的时间复杂度为O(n^2)，虽然复杂度还可以，但是仍可以优化。

解法二：递归+剪枝化

我们可以设置一个记忆集(memory)，来记录第i个字符到第j个字符是否是回文串。这样当检查字串时，先检查memory，如果有记录就返回。没有再去递归检查。

class Solution {
    Integer[][] memory;
	public String longestPalindrome(String s){
		int n = s.length();
		int start = 0;
		int len = 0;
        memory = new Integer[n][n];
		for(int i = 0; i < n; i++){	
			for(int j = i; j < n; j++){
			//验证第i个字符到第j个字符组成的字符串是否是回文串
			//如果是回文串，则验证是否更新了已记录的最长记录
				if(checkPalindrome(s,i,j)){
					if(j-i+1 > len){
						len = j - i + 1;
						start = i;
					}
				}
			}	
		}
		return s.substring(start,start+len);
	}
	public boolean checkPalindrome(String s, int begin, int end){
		if(begin >= end){
			return true;
		}
		//记忆集中是否有记录
		if(memory[begin][end] != null){
			//false:不为回文串
			//true:回文串
			//null:无记录
			return memory[begin][end] == 0 ? false : true;
		}
		if(s.charAt(begin)==s.charAt(end)){
			//是回文串
            if(checkPalindrome(s,begin+1,end-1)){
                memory[begin][end] = 1;
                return true;
            }
            //不是回文串
			memory[begin][end] = 0;
			return false;
		}
		memory[begin][end] = 0;
		return false;
	}	
}

解法三：动态规划

从上面的解题思路可以得知，在起点字符与终点字符相同情况下，字符串是否是回文串的关键在于起点下一个字符串与终点前一个字符串是否也相同…
因此我们可以通过动态规划来解决。
二维数组dp[i][j]:代表第i个字符到第j个字符是否是回文串。

状态转移方程:
if(s.charAt(i) == s.charAt(j)) dp[i][j] = dp[i+1][j-1]。

dp[i][j]的值与dp[i+1][j-1]相关，因此要想获取dp[i][j]的状态，必须先获取后值。为此遍历的方向与之前几个解法不同，改为从后向前遍历。

class Solution {
	public String longestPalindrome(String s){
		int n = s.length();
		int start = 0;
		int len = 0;
		boolean[][] dp = new boolean[n][n];
		//遍历从最后一个字符开始
		for(int i = n-1; i >= 0; i--){
			//起点字符和终点字符指向同一个字符
			dp[i][i] = true;	
			for(int j = i; j < n; j++){
				//起点字符和终点字符相同相同
				if(s.charAt(i) == s.charAt(j)){
					if(i+1>j-1 || dp[i+1][j-1]){
						dp[i][j] = true;
						if(j-i+1>len){
							start = i;
							len = j-i+1;
						}
					}
				}else{
                    dp[i][j] = false;
                }
			}	
		}
		return s.substring(start,start+len);
	}
}

leetcode561:最长回文子序列

你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。
输入：s = “bbbab”
输出：4
解释：一个可能的最长回文子序列为 “bbbb” 。

解题思路与回文子串类似，先保持起点坐标不变，不断变化终点坐标…不同点在于不再计算子回文串，而是计算子序列。
1）：在起点字符与终点字符相同的情况下，字符串的最长回文子序列长度为更新起点与终点后构成的最长回文子序列长度+2。

2）：在起点字符与终点字符不相同的情况下，字符串的最长回文子序列长度为只更新起点与只更新终点的回文子序列长度的最大值。

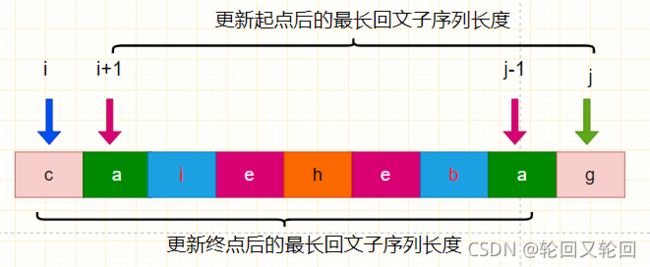
解法一：递归+剪枝化

class Solution {
    int[][] memo;
    public int longestPalindromeSubseq(String s) {
		int n = s.length();
		memo = new int[n][n];
		int res = 0;
		for(int i = 0; i < n; i++){
			for(int j = i; j < n; j++){
				checkPalinSubseq(s,i,j);
			}
		}
		return checkPalinSubseq(s,0,n-1);
	}
	public int checkPalinSubseq(String s, int start, int end){
		//起点与终点相同
		if(start == end) return 1;
		//起点与终点不相同
		if(start > end) return 0;
		//记忆化剪枝
		if(memo[start][end] != 0) return memo[start][end];
		//起点与终点字符相同
		if(s.charAt(start) == s.charAt(end)) memo[start][end] = 2 + checkPalinSubseq(s,start+1,end-1);
		//起点与终点字符不相同
		else{
			memo[start][end] = Math.max(checkPalinSubseq(s,start+1,end),checkPalinSubseq(s,start,end-1));
		}
		return memo[start][end];
	}
}	

解法二：动态规划

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] dp = new int[n+1][n+1];
        //第i个字符到第j个字符的最长回文子序列
        for(int i = n-1; i >= 0; i--){
            dp[i][i] = 1;
            for(int j = i+1; j < n; j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }
                else{
                    dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
                }
            }
        }
        return dp[0][n-1];
    }
}